The Gaseous State, Ideal and Real Gases and pV = nRT
Quick Notes
- Gas pressure is caused by collisions of gas particles with the walls of the container.
- An ideal gas assumes:
- Particles of the gas have no volume
- There are no intermolecular forces
- Ideal gas equation: pV = nRT where:
- p = pressure (Pa)
- V = volume (m³)
- n = number of moles
- R = gas constant = 8.31 J mol⁻¹ K⁻¹
- T = temperature (K)
Full Notes
Pressure in a Gas
Gas pressure arises from the continuous collisions of gas molecules with the walls of the container.
- Gas particles are in random, rapid motion.
- When particles collide with the walls, they exert a force.
- The total force of all these collisions, spread over the surface area of the container, creates pressure.
- More frequent and energetic collisions = higher pressure.
Ideal Gas Assumptions
An ideal gas is a simplified model that allows easy calculations. It is based on two key assumptions:
- Gas particles have no volume
- The particles themselves are considered point-sized.
- The volume of the gas is due only to the space between the particles.
- There are no intermolecular forces
- Particles do not attract or repel each other.
- They move in straight lines until they collide.
Breakdown of Ideal Gas Assumptions
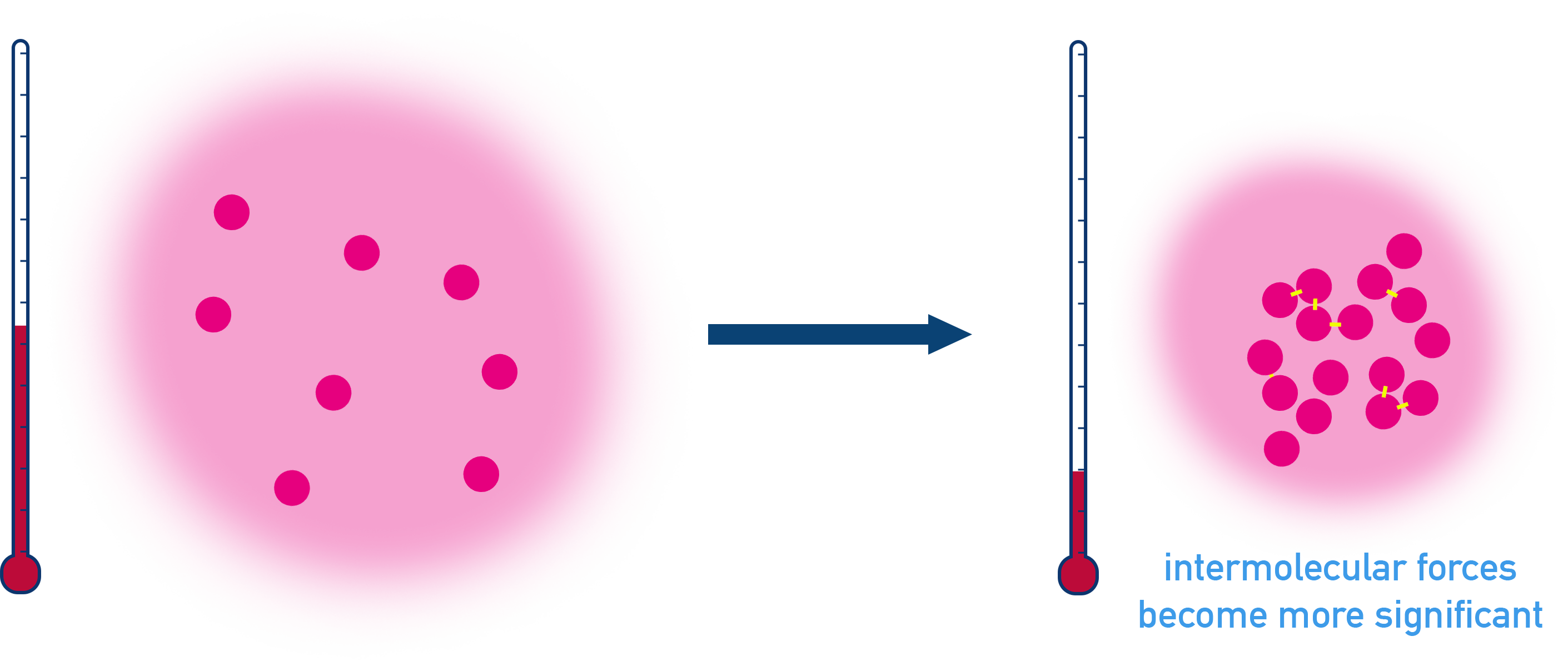
The above assumptions for ideal gases are not fully true for real gases, especially at high pressure or low temperature (but are useful for most calculations under standard conditions).
- At high pressures, gas particles occupy space, meaning their volume is no longer negligible.
- At low temperatures, intermolecular forces become significant, making gases more likely to condense.

The Ideal Gas Equation
The ideal gas equation links pressure, volume, temperature and moles of gas:

Where:
- p = pressure (Pa)
- V = volume (m³)
- n = number of moles
- R = gas constant = 8.31 J mol⁻¹ K⁻¹
- T = temperature in Kelvin (K)
To convert:
- cm³ → m³: divide by 1 000 000
- dm³ → m³: divide by 1000
- °C → K: add 273
Using the Ideal Gas Equation
a) Calculating moles
Rearrange the equation: n = pV ÷ RT
This is useful to find:
- Number of moles of gas
- Molar mass (Mr), using Mr = mass ÷ moles
Find the moles of gas in a container, given: p = 101 000 Pa, V = 0.025 m³, T = 298 K, R = 8.31 J mol⁻¹ K⁻¹.
- Answer: moles of gas = (101000 × 0.025) ÷ (8.31 × 298) ≈ 1.02 mol
b) Calculating molar mass (Mr)
Use this formula: Mr = mass × R × T ÷ (p × V)
This is especially useful when determining Mr from experimental gas data.
Calculating Molar Mass (Mr) Using pV = nRT
To find the molar mass (Mr) of a gas, rearrange the ideal gas equation:
- Use pV = nRT
- n = mass ÷ Mr
- Substitute into the equation: pV = (mass ÷ Mr) × RT
- Rearranged: Mr = (mass × R × T) ÷ (p × V)
A 0.39 g sample of a gas occupies 300 cm³ at a pressure of 100 kPa and a temperature of 20°C. Calculate its molar mass (Mr).
- Convert all units to SI
Volume: 300 cm³ = 0.000300 m³
Pressure: 100 kPa = 100000 Pa
Temperature: 20°C = 293 K
R = 8.31 J mol⁻¹ K⁻¹ - Plug into the formula
Mr = (0.39 × 8.31 × 293) ÷ (100000 × 0.000300)
Mr = (0.39 × 2436.83) ÷ 30
Mr = 950.36 ÷ 30 = 31.7 g mol⁻¹ - Answer: The molar mass of the gas is approximately 31.7 g mol⁻¹.
Summary
- Gas pressure is caused by collisions of particles with container walls.
- Ideal gas assumptions:
- Particles have no volume
- No intermolecular forces
- Ideal gas equation: pV = nRT.
- At high pressure and low temperature, real gases deviate from ideal behavior.
- Rearranging pV = nRT allows calculation of moles and molar mass (Mr).
- Always convert units correctly: cm³ → m³, °C → K.
