Lattice energy and Born–Haber cycles

Full Notes

Lattice enthalpies and Born–Haber cycles have been outlined in more detail here.
This page is just what you need to know for CIE A-level Chemistry :)

Lattice energy (ΔH_latt) refers to the energy change associated with the formation of an ionic solid from its gaseous ions. It can be considered a measurement of the bonding strength in ionic compounds.

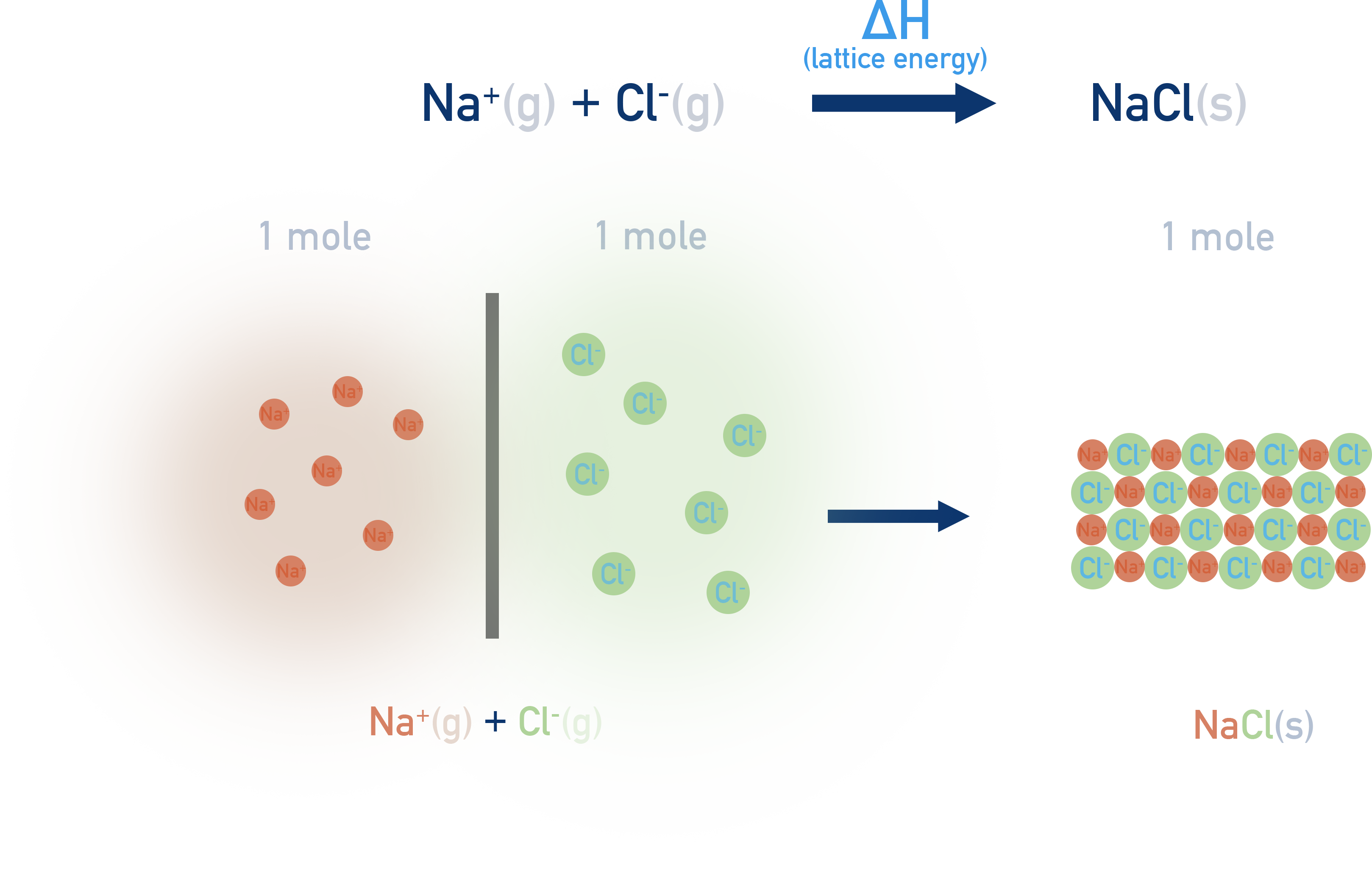
Lattice energies can’t be measured directly in an experiment however can be determined using experimental data with Hess’s Law.

Born–Haber cycles are a type of Hess cycle used to calculate lattice energy.

Key Definitions

Enthalpy change of atomisation (ΔH_at):
The enthalpy change when 1 mole of gaseous atoms is formed from an element in its standard state.
Example: Na(s) → Na(g)

Lattice energy (ΔH_latt):
The enthalpy change when 1 mole of an ionic solid is formed from its gaseous ions.
Example: Na⁺(g) + Cl⁻(g) → NaCl(s)
Lattice energy is always exothermic (negative value).

Electron Affinity

• First electron affinity is the energy change when 1 mole of gaseous atoms gains electrons to form 1 mole of 1⁻ ions.
  Example: Cl(g) + e⁻ → Cl⁻(g)
  This is usually exothermic.
• Second electron affinity is for adding an electron to a negatively charged ion (e.g. O⁻ to O²⁻), and is endothermic due to repulsion.

Constructing a Born–Haber Cycle

1. Write the enthalpy of formation equation (solid compound from elements).
2. Convert elements to gaseous atoms (atomisation enthalpy).
3. Remove electrons from metal atoms (ionisation energy).
4. Add electrons to non-metal atoms (electron affinity).
5. Combine gaseous ions to form lattice (lattice enthalpy).

Example Born–Haber Cycle for NaCl

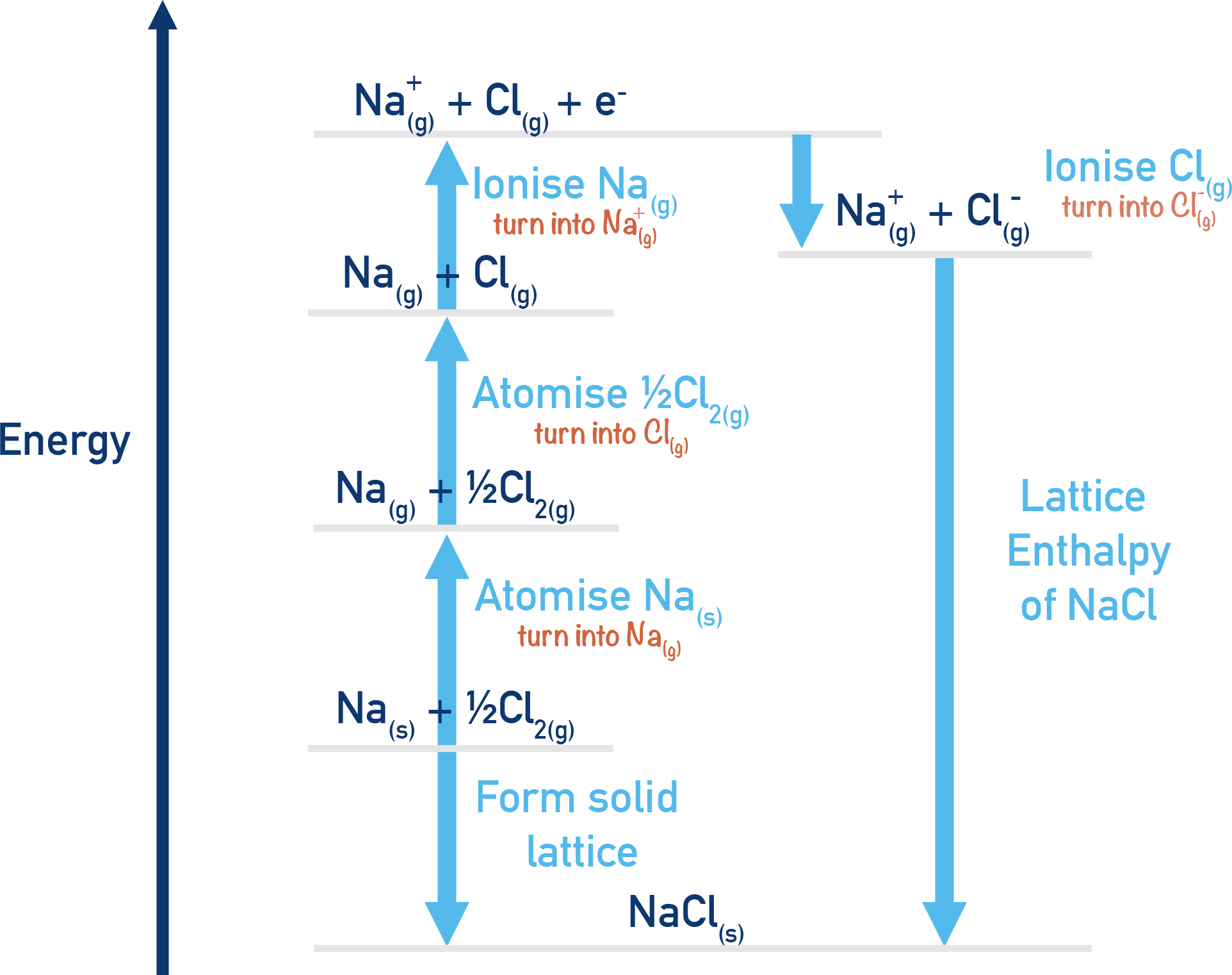
• Step 1: Formation of NaCl (ΔH_f)
  Na(s) + ½Cl₂(g) → NaCl(s)
• Step 2: Atomisation of Na (ΔH_atom)
  Na(s) → Na(g)
• Step 3: Atomisation of Cl₂ (ΔH_atom)
  ½Cl₂(g) → Cl(g)
• Step 4: Ionisation Energy of Na (IE₁)
  Na(g) → Na⁺(g) + e⁻
• Step 5: Electron Affinity of Cl (EA₁)
  Cl(g) + e⁻ → Cl⁻(g)
• Step 6: Lattice Enthalpy (ΔH_le)
  Na⁺(g) + Cl⁻(g) → NaCl(s)

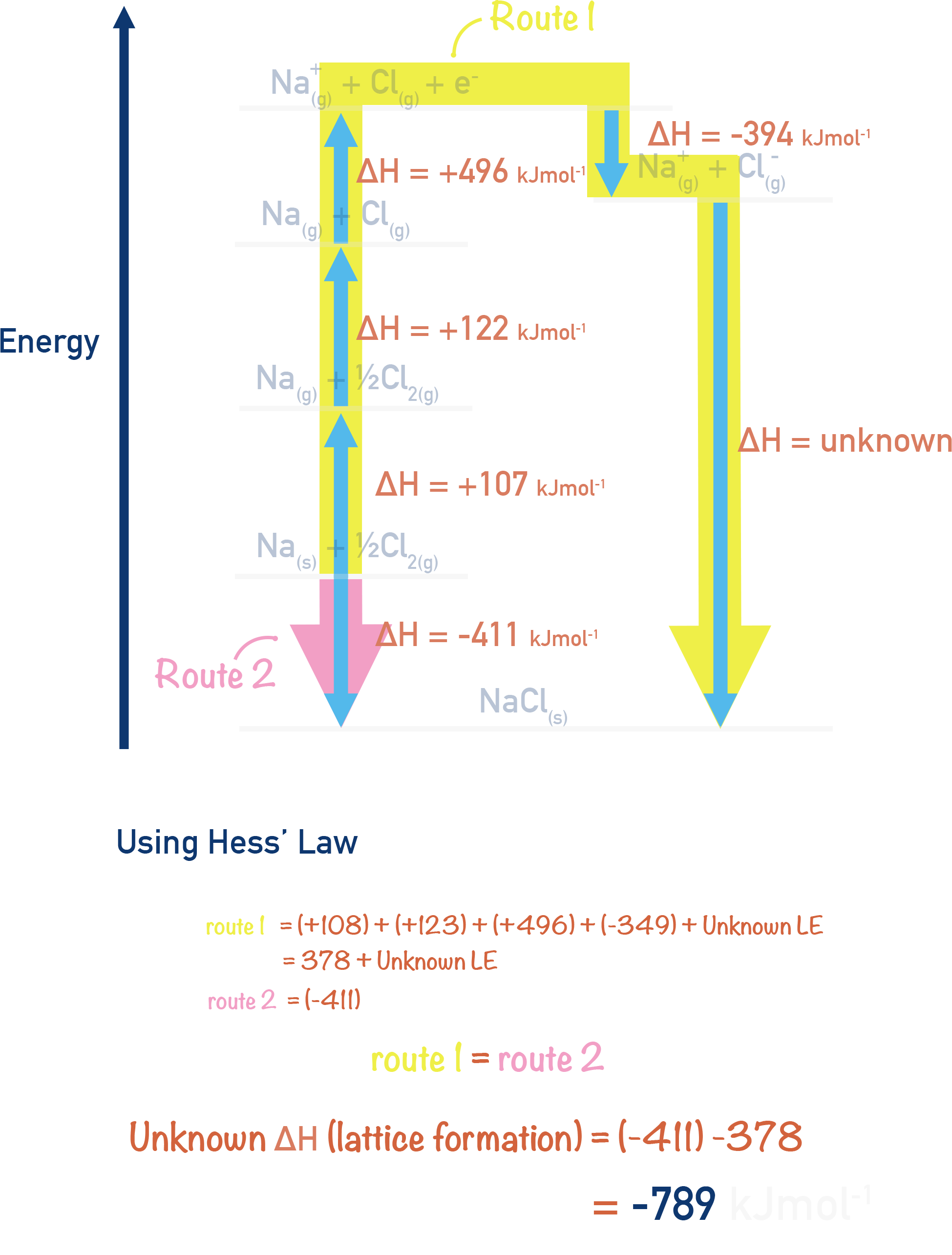
By rearranging these enthalpy changes and substituting experimental values into the cycle we can use Hess’s Law to calculate ΔH_le.

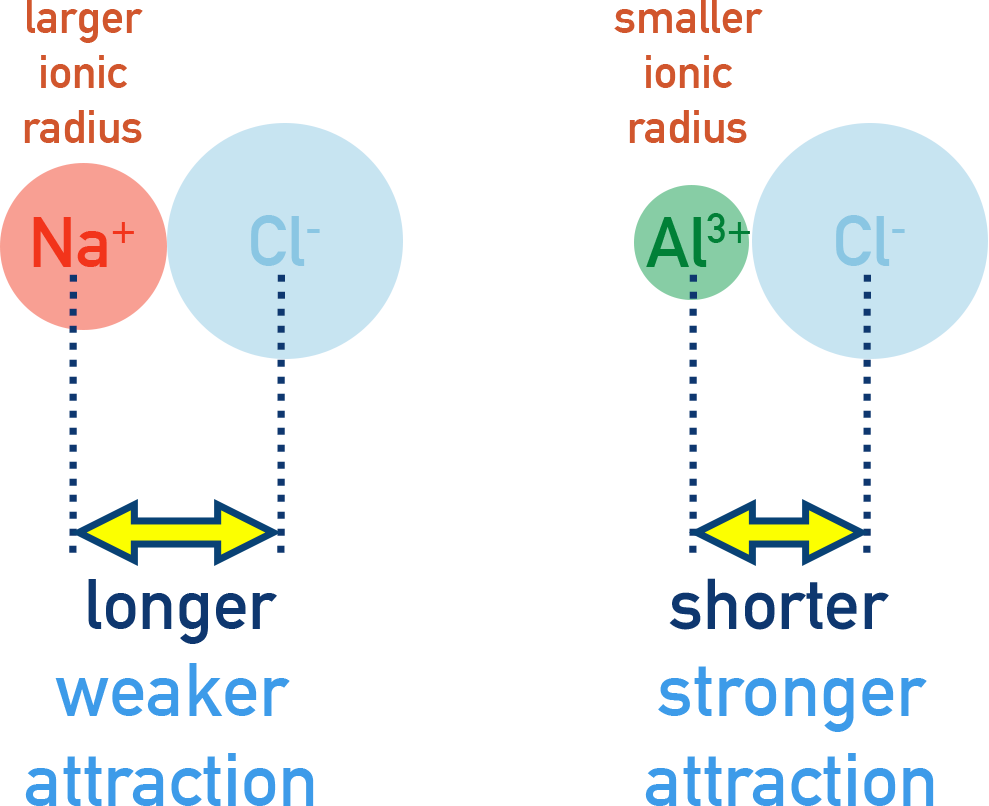
Factors Affecting Lattice Energy

Charge and ionic radius affects the magnitude of lattice energy

• Charge: Higher ion charge = stronger electrostatic attraction between ions = more exothermic lattice energy.
  Example: Mg²⁺ forms more exothermic lattices than Na⁺.
• Ionic radius: Smaller radius = stronger attraction = more exothermic lattice energy.
  Down a group, ionic radius increases and lattice energy becomes less exothermic.

Trends

• Group 17 elements have more exothermic electron affinities than Group 16.
• Down the group, electron affinities become less exothermic due to increasing atomic radius and electron shielding.

Summary

• ΔH_at: enthalpy change of atomisation forms gaseous atoms from elements.
• ΔH_latt: lattice energy forms ionic solid from gaseous ions (always exothermic).
• Born–Haber cycles apply Hess’s Law to calculate lattice energy.
• Electron affinity: first usually exothermic, second usually endothermic.
• Lattice energy depends on ionic charge and radius (higher charge and smaller radius = more exothermic).
• Electron affinities less exothermic down a group due to increased shielding and atomic size.