Video Tutorial Lattice Enthalpies
Quick Notes Lattice Enthalpies
- Lattice enthalpy of formation is the enthalpy change that occurs when 1 mole’s worth of an ionic compound is formed from its constituent, free gaseous ions.
- Lattice formation enthalpies are always negative, -ΔH (exothermic process).
- When two oppositely charged ions come close together their energies lower, releasing energy to the surroundings.
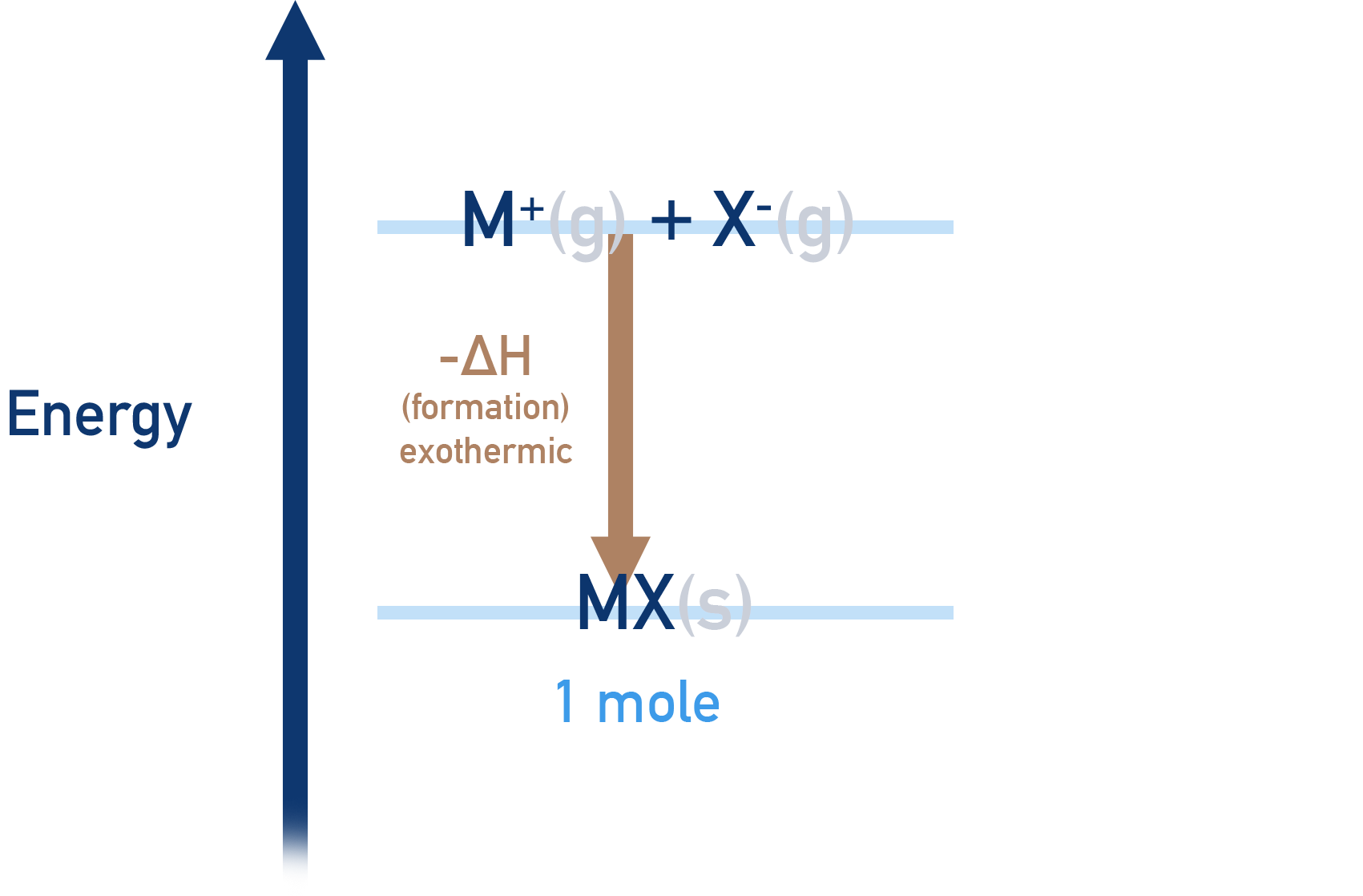
- Lattice enthalpy of dissociation is the enthalpy change that occurs when 1 mole’s worth of an ionic lattice is broken apart into free gaseous ions.
- Lattice dissociation enthalpies are always positive, +ΔH (endothermic process).
- To pull oppositely charged ions apart requires energy and this means the ions energies increase.
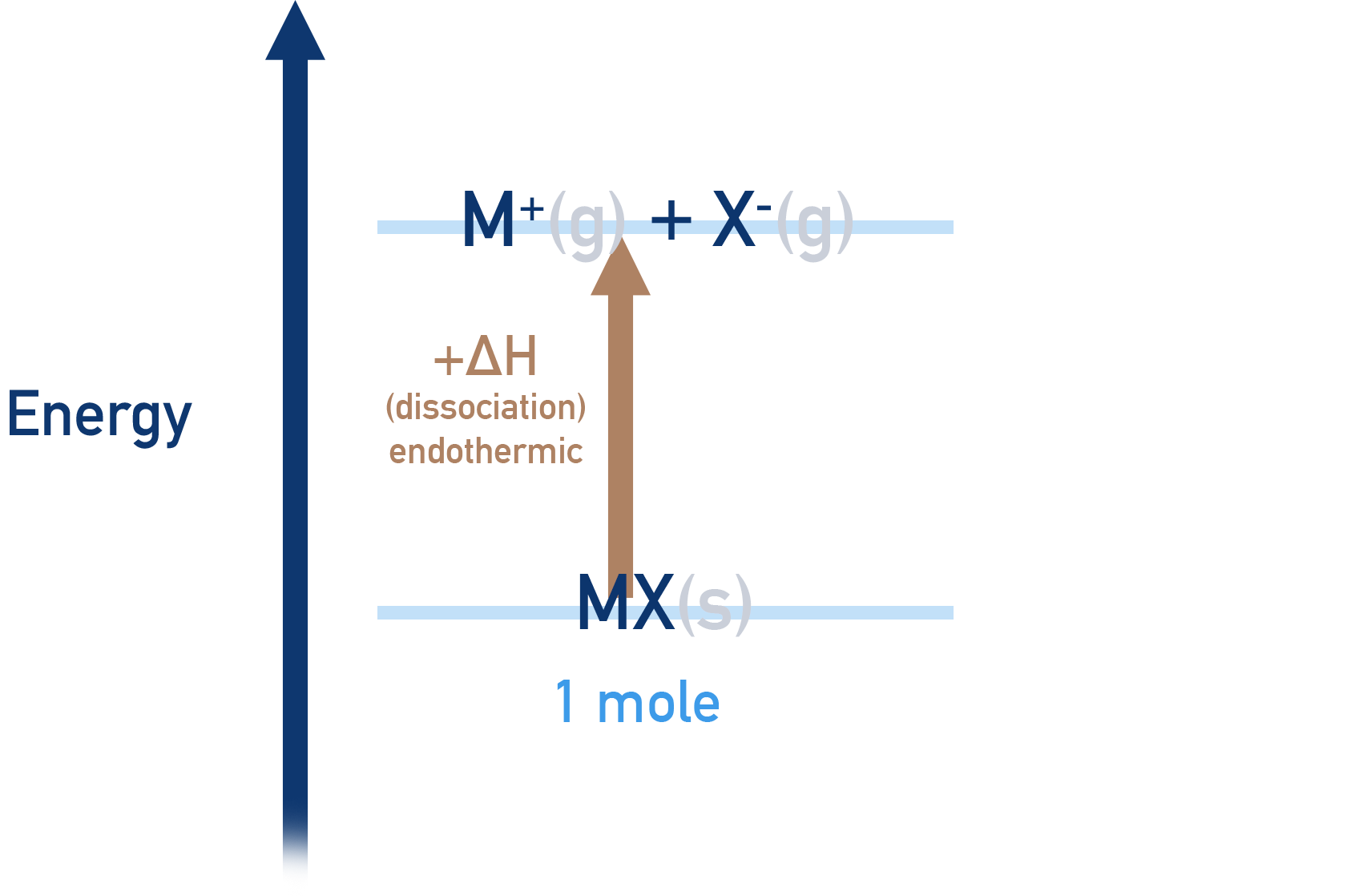
- Solid ionic lattices are held together by strong electrostatic attraction between oppositely charged ions.
- Ion charge and size influence the strength of attraction.
- The smaller the ionic radius and the greater the charge, the stronger the attraction.
- The stronger the attraction between ions, the stronger the lattice (higher melting point).
- Lattice enthalpies cannot be measured directly, they have to found using Hess's Law and Born-Haber cycles.
Full Notes Lattice Enthalpies
When in solid state, ionic compounds have a lattice structure. These lattice structures are held together by strong electrostatic forces of attraction between oppositely charged ions.
Lattice enthalpies are used to describe the strength of attraction within a lattice (a bit like bond enthalpies can be used to describe the strength of a covalent bond).
The stronger the attraction between ions, the stronger the ionic lattice, making it harder to break apart. The weaker the attraction between the ions, the easier it is to break the lattice apart. See Ionic Bonding.
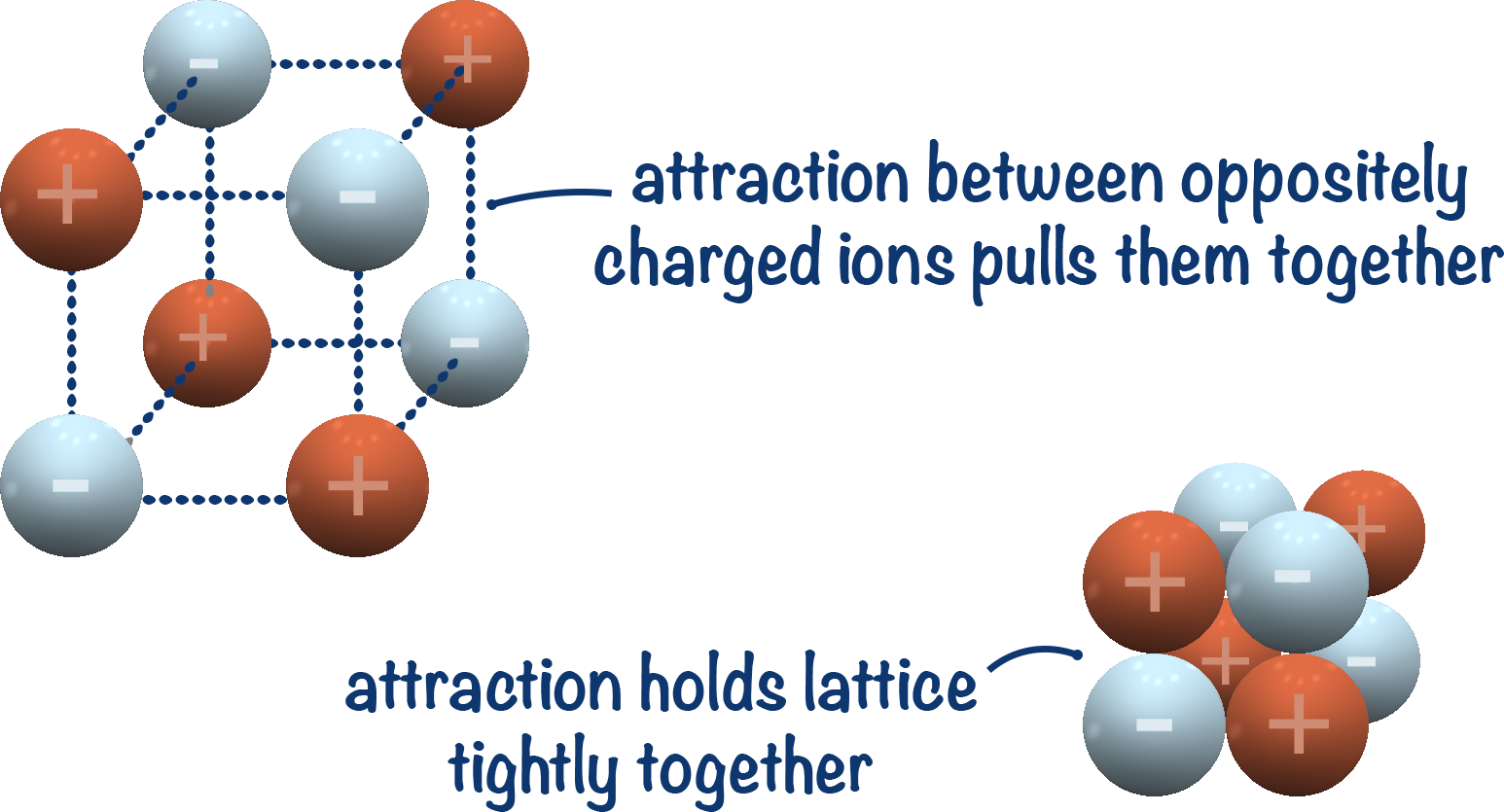
Ionic lattices are generally very stable, and when they are formed energy is released. Charged ions are high energy species. By moving two oppositely charged ions closer, their energy decreases. This means energy is released by the charged ions as they ionically bond to each other.
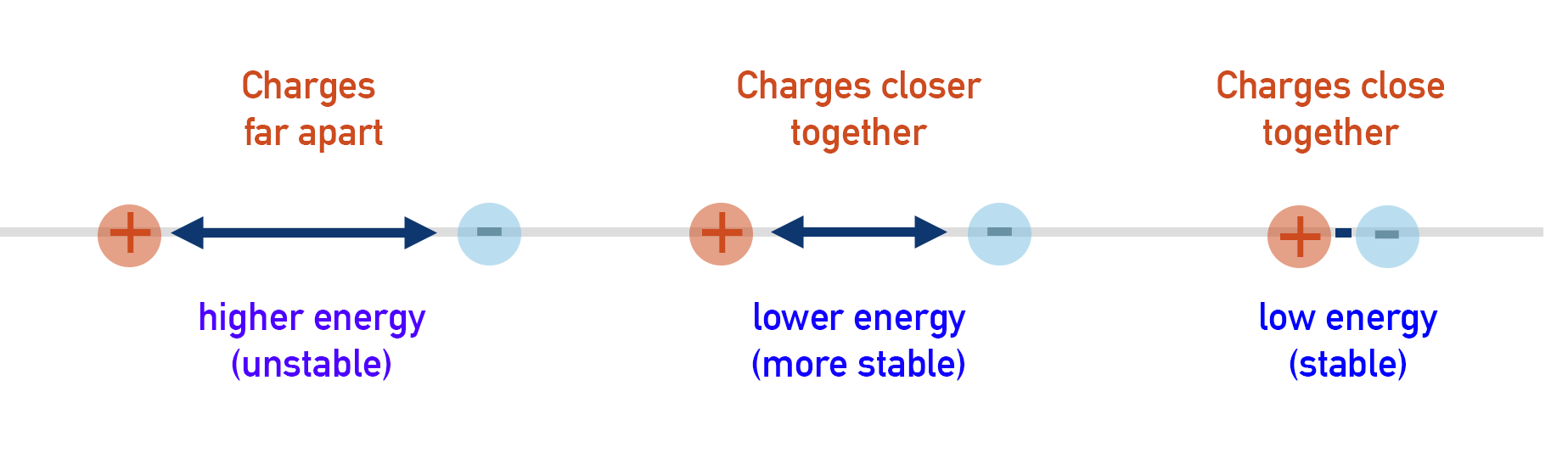
The closer the oppositely charged ions can get to each other, the more stable they become and the more energy they release.
Lattice enthalpies show how much energy is released when a lattice is formed from free gaseous ions or how much energy is required to split apart a lattice back into gaseous ions. In other words, the difference in energy between free gaseous ions and the lattice they can combine to form.

To make things clearer, we usually refer to lattice enthalpies of formation and lattice enthalpies of dissociation rather than the general term 'lattice enthalpy'.
Lattice Enthalpies of Formation
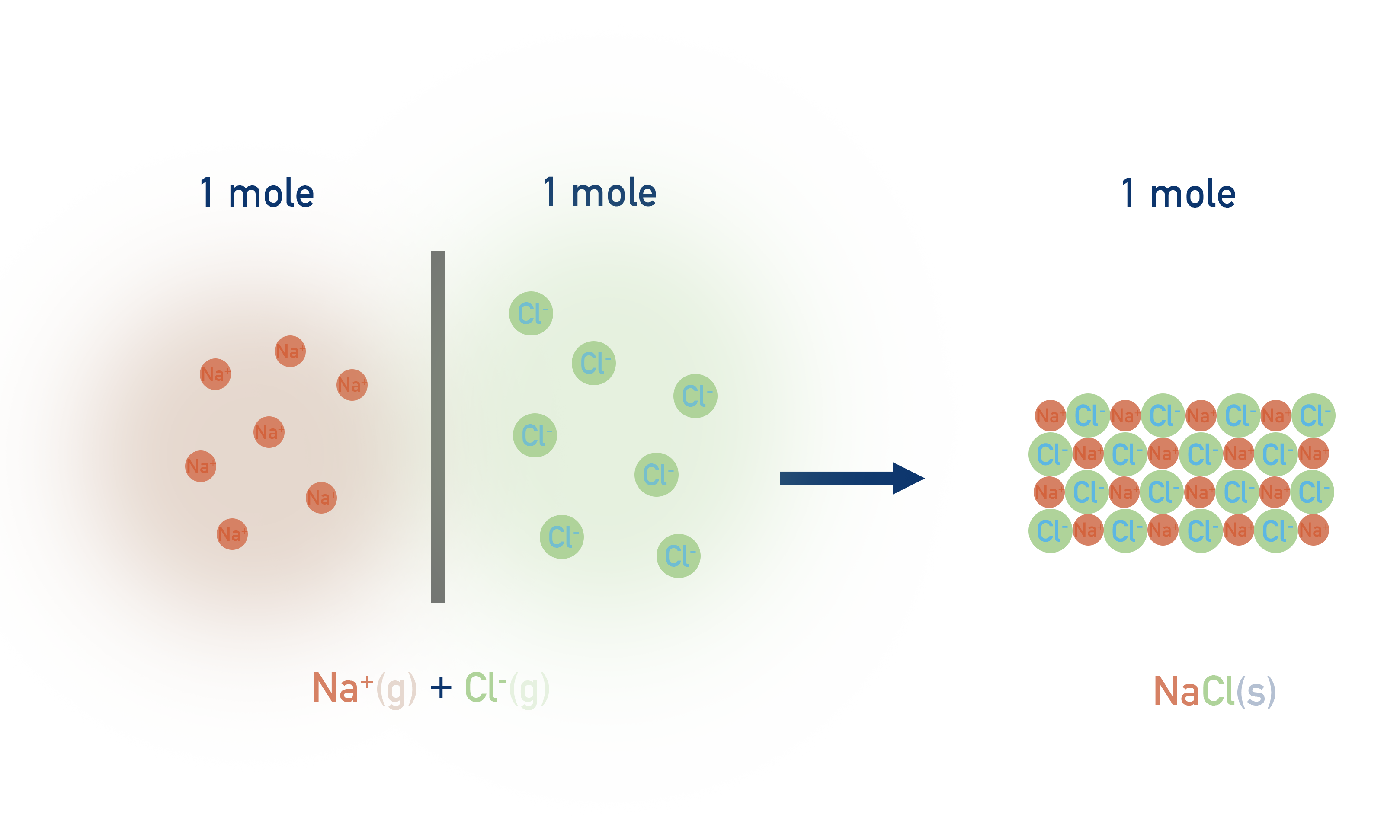
If oppositely charged, gaseous ions are mixed together, they will form a stable ionic lattice.
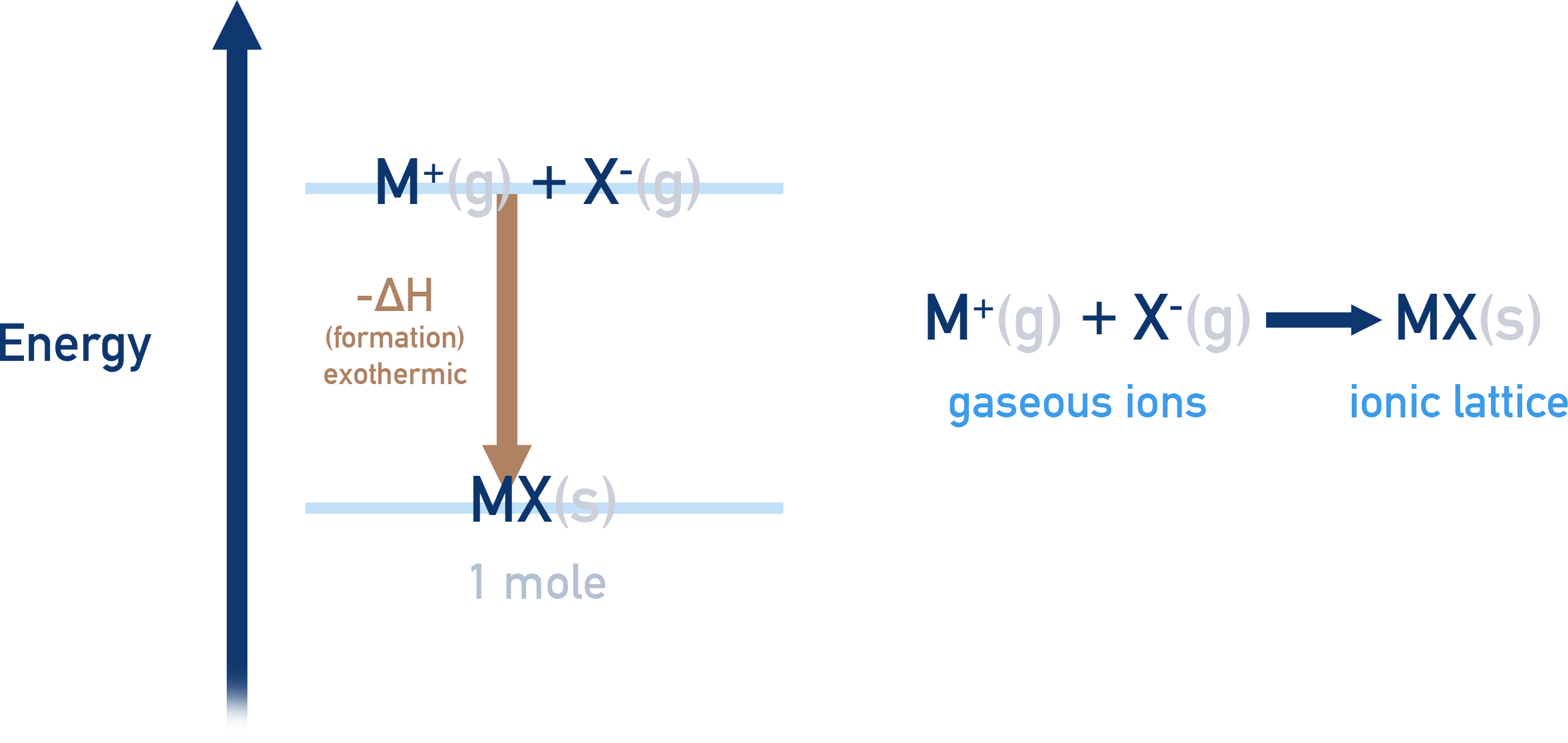
The ionic lattice will be much lower in energy than the ions that formed it. As a result, the ions must lose energy as they form the lattice. This makes lattice formation an exothermic process with a negative enthalpy change (-ΔH).
Lattice enthalpy of formation, ΔH⦵LE formation
The enthalpy change that occurs when 1 mole of an ionic compound is formed from its constituent, free gaseous ions under standard conditions.
The amount of energy released as a lattice forms is based on the size and charge of the ions (see below).
Lattice Enthalpies of Dissociation
To break an ionic lattice apart (dissociation), energy is needed.
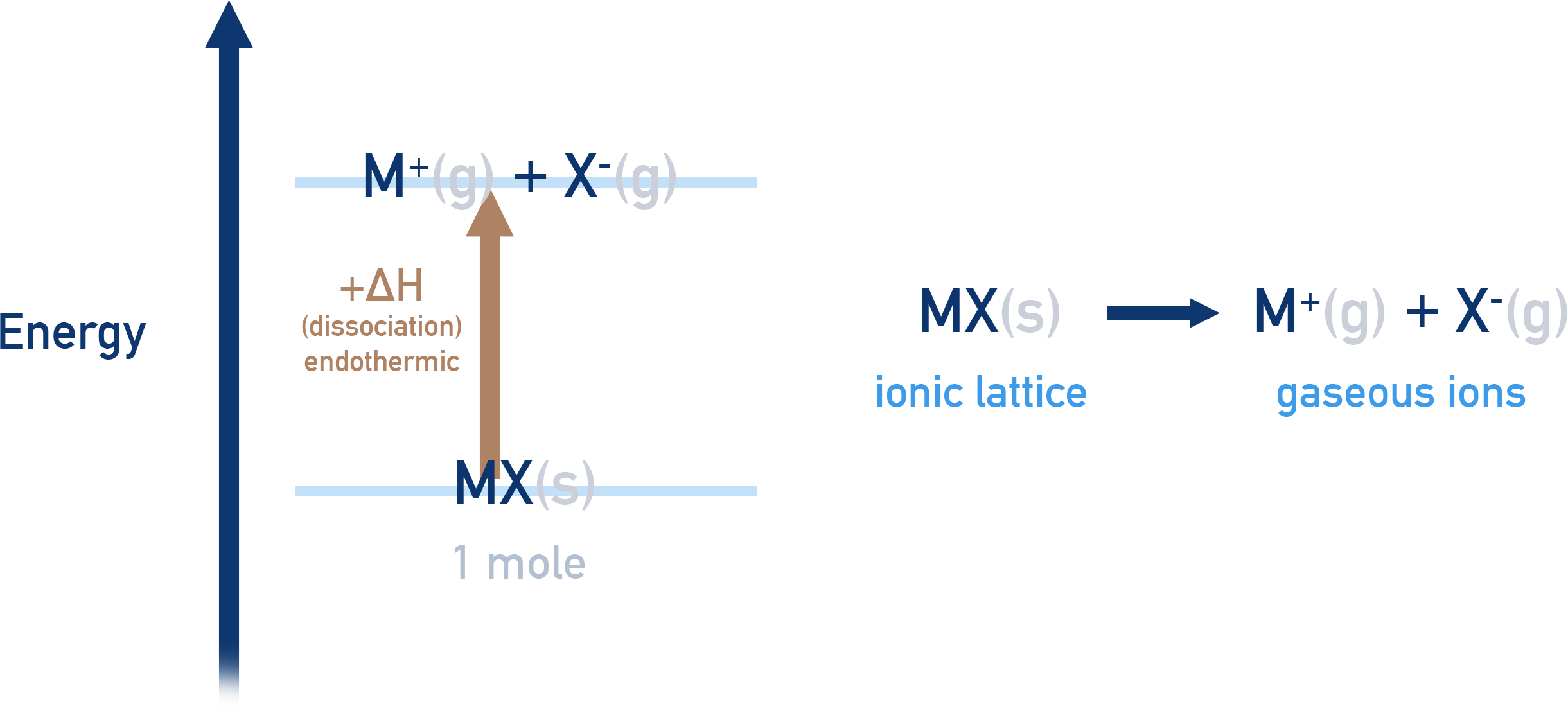
In order to overcome the forces of attraction holding them together, the oppositely charged ions have to be given energy, meaning their enthalpy increases. This makes lattice dissocation an endothermic process with a positive enthalpy change (+ΔH).
Lattice enthalpy of dissociation, ΔH⦵LE dissociation
The enthalpy change that occurs when 1 mole of an ionic compound is split apart completely into free, gaseous ions, under standard conditions.
The amount of energy needed to split apart a lattice into free gaseous ions is exactly the same as the amount of energy released when the same gaseous ions form a lattice. As a result, for any given lattice, its standard lattice enthalpy of formation will have the same value as its standard lattice enthalpy of dissociation. The only difference will be the - and + signs (- for formation, + for dissociation).
Size of Lattice Enthalpies
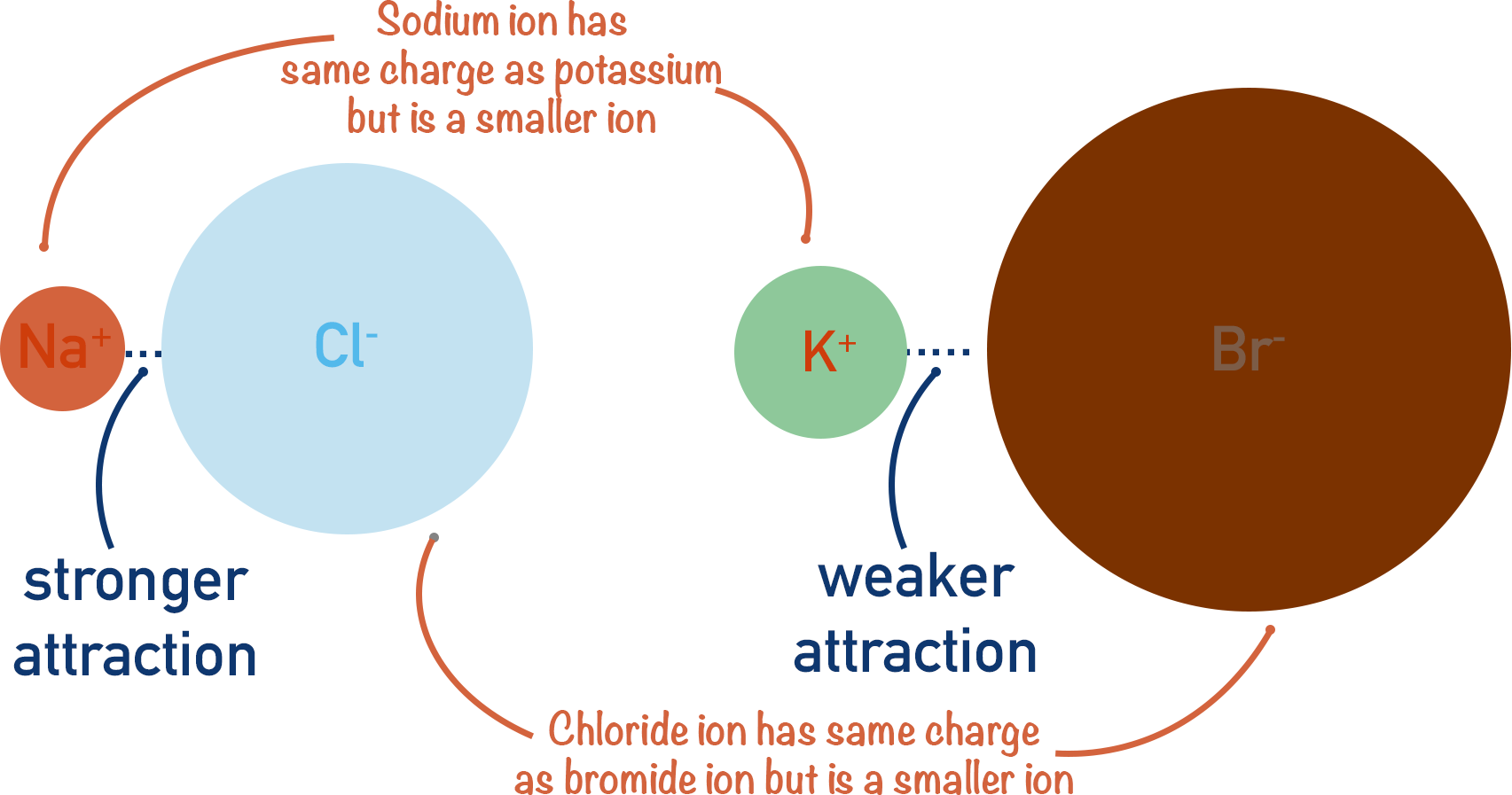
There are two factors that determine the strength of attraction between oppositely charged ions - the charges of the ions and their sizes. For more detail on this, see Ionic Bonding.
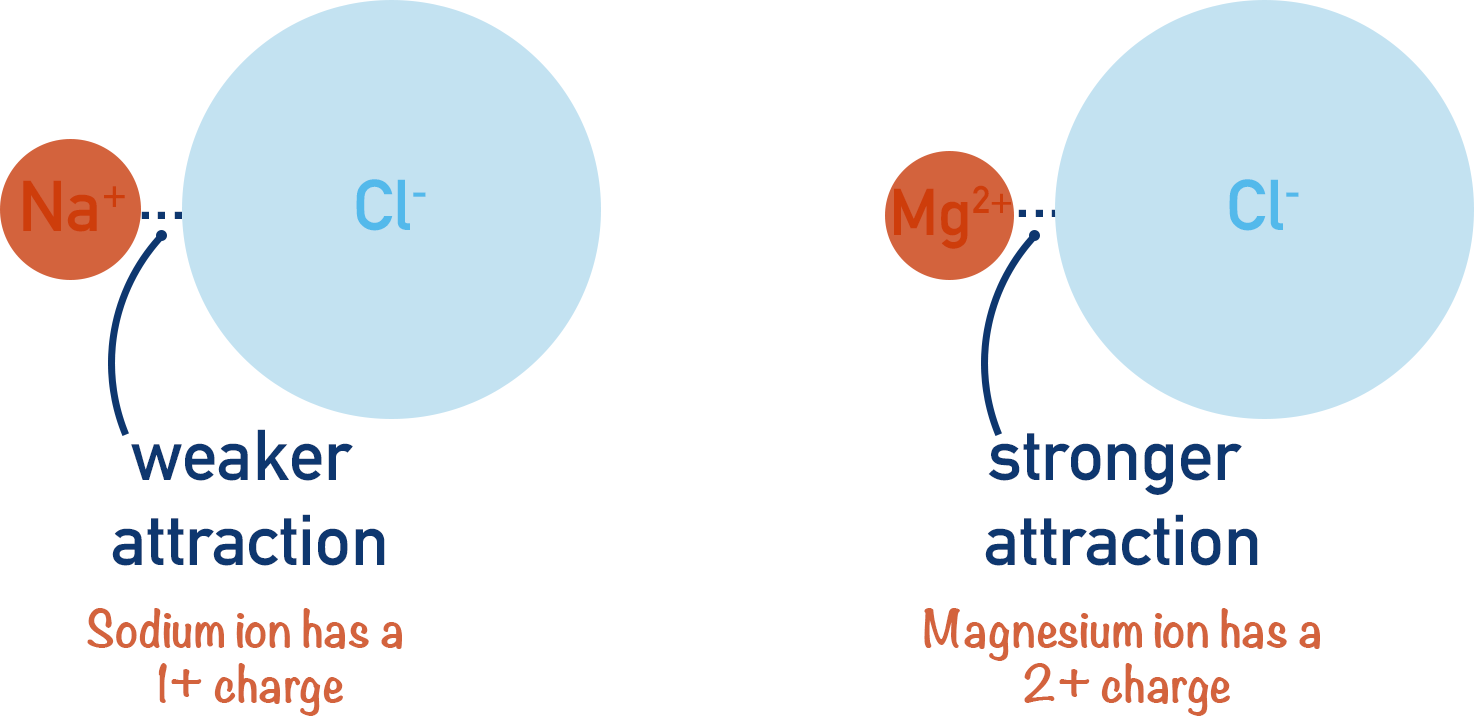
The greater the difference in charge between the ions, the stronger the attraction between them.
The larger the ions get, however, the weaker the attraction as there is a greater distance between the positively charged nucleus of one ion and the negative charge (electrons) of the other.
Charge density refers to how the charge of the ion compares to the size (or mass) of the ion. High charge densities of ions give strong ionic attraction.
Note - covalent character within a lattice means that the forces holding the lattice together are no longer just ionic interactions. In such cases, experimental lattice enthalpies can differ from expected (theoretical) values.
Why can't lattice enthalpies be measured directly?
Lattice enthalpies cannot be measured directly. To find them experimentally, Hess's law needs to be used with Born-Haber cycles (see Born-Haber cycles).
The problem is that lattice enthalpies refer to the difference in energy between oppositely charged free, gaseous ions and the lattice they combine to form.
To measure this difference directly you would need to keep the charged ions apart and then mix them together in their molar ratios perfectly and measure the enthalpy change taking place. Imagine trying to keep exactly 1 mole of Na+ and 1 mol of Cl- gaseous ions apart and then mixing them together perfectly and finding the energy change taking place! Impossible.
As a result of this, the only way to determine such enthalpy changes is indirectly, based on Hess's Law (see Hess's Law).
Lattice enthalpies can also be predicted based on the sizes and charges of the ions in the lattice. Such enthalpies are reffered to as 'theoretical' values as they arn't based on experimental data (unlike those used when finding such changes using Born-haber cycles). As a result, there can be differences in theoretical lattice enthalpy and experimental lattice enthalpy values. This is due to the fact that theoretical values only take ionic attraction into account, they don't allow for covalent character within a compound (see Covalent Character).
We’ve launched our new site! 🎉
Course-specific notes with built-in search!
AP • A-Level (AQA • CIE • Edexcel • OCR) • IB • NCERT 11 + 12
over 750+ new pages and 3,500 images.
Visit the new homepage
