Acids and bases

Full Notes

Acid-Base theory has been covered in more detail here.
This page is just what you need to know for CIE A-level Chemistry :)

Conjugate Acids and Bases

A conjugate acid–base pair consists of two species that differ by a single proton (H⁺).

When an acid donates a proton, the conjugate base is what remains after the acid has lost a proton.

Example: HCl → Cl⁻ + H⁺
Here, HCl is the acid and Cl⁻ is its conjugate base.

Tracking conjugate pairs helps us follow proton transfer in acid–base reactions.

Identifying Conjugate Pairs

In any acid–base reaction:

• The acid and its conjugate base differ by one H⁺.
• The base and its conjugate acid differ by one H⁺.

Example:
NH₄⁺ ⇌ NH₃ + H⁺
NH₄⁺ acts as the acid (donates H⁺).
NH₃ is the conjugate base (can accept H⁺).

Matt’s exam tip

When trying to determine conjugate pairs, always look for whether a proton has been lost or gained. Don’t worry about the rest of the formula or how complicated something might look, you are only interested in whether it has gained or lost a H+ ion!

pH

pH is a scale used to represent the concentration of H⁺ ions ([H⁺]) in a solution. It is a log scale and can be calculated using

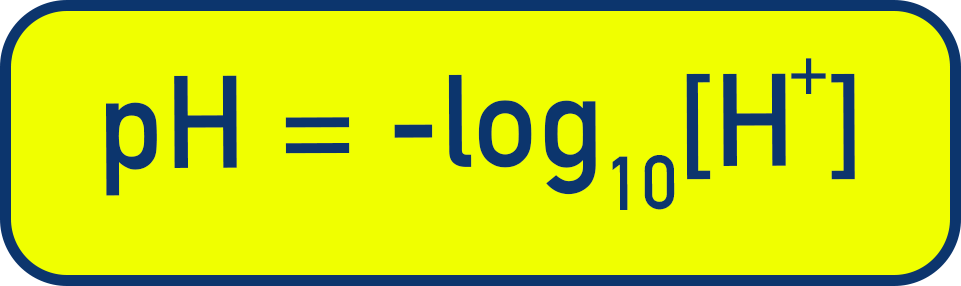
• (A lower pH = higher H⁺ concentration = more acidic.)

Ka, pKa, and Kw

K_a

Ka is the acid dissociation constant for a weak acid: it measures how much a weak acid ionises in solution.

• Larger Ka = Stronger weak acid (more dissociation).
• Smaller Ka = Weaker acid (less dissociation).

pK_a

pKa is a log scale used to represent Ka values. It can be calculated using

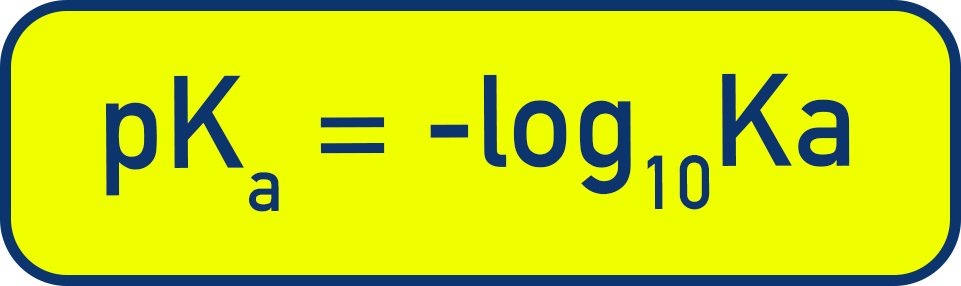
• Smaller pKa → Stronger acid.

K_w

K_w is the ionic product of water (covered in more detail here):

At 298 K, K_w = 1.00 × 10⁻¹⁴ mol² dm⁻⁶.
These relationships allow you to calculate pH and predict acid strength.

Calculating [H⁺] and pH Values

You need to be comfortable calculating pH and [H⁺].

Strong Acids:

• Completely dissociate.
• [H⁺] = initial acid concentration.

Strong Bases:

• Completely dissociate.
• Calculate [OH⁻] first, then: [H⁺] = Kw ÷ [OH⁻]
  Then find pH.

Weak Acids:

• Only partially dissociate.
• Use Ka = [H⁺]² / [HA]
  (Assuming [H⁺] = [A⁻])
  Then pH = –log[H⁺].

Buffer Solutions

What is a Buffer?
A buffer is a solution that resists changes in pH when small amounts of acid or base are added.

How to Make a Buffer

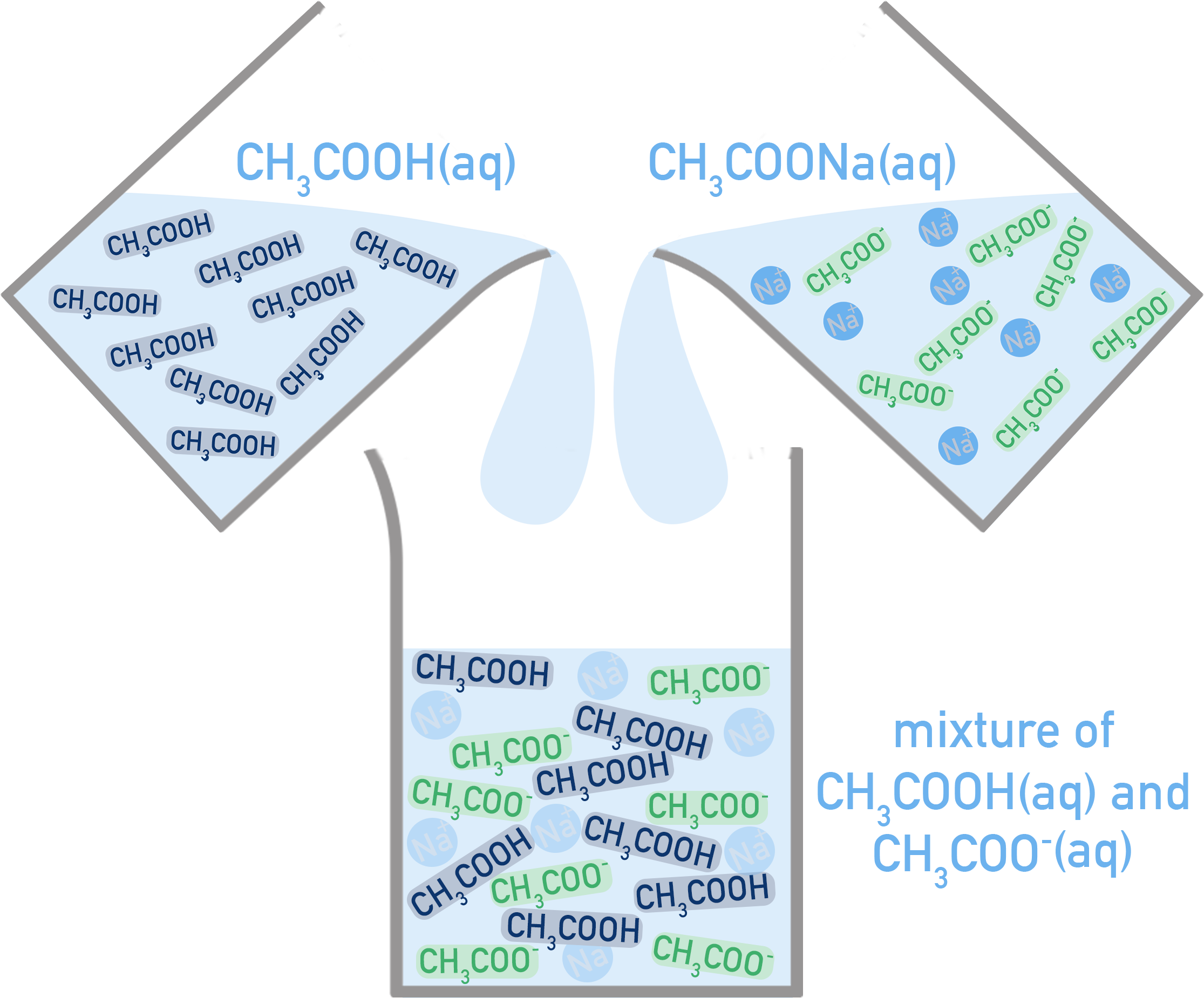
• Acidic buffer: Weak acid + its salt (e.g., CH₃COOH + CH₃COONa).
  Note that you can also make an acidic buffer by adding a strong base to an excess of weak acid (end up with a mixture of weak acid and salt).


• Basic buffer: Weak base + its salt (e.g., NH₃ + NH₄Cl).
  Note that you can also make a basic buffer by adding a strong acid to an excess of weak base (end up with a mixture of weak base and salt).

Both the weak acid/base and its conjugate must be in large amounts relative to [H⁺].

How Buffers Work (Acidic Buffers)

An equilibrium is established in the buffer system between HA, A⁻ and H⁺.

The concentration of HA and A⁻ in the mixture must be much greater than the concentration of H⁺. This ensures the position of equilibrium is sensitive to changes in H⁺ concentration change more than changes to HA and A⁻ concentration. Equilibrium position can shift to keep H⁺ ion concentration nearly constant.

Example: Ethanoic Acid/Sodium Ethanoate Buffer (CH₃COOH/CH₃COO⁻)

Equilibrium reaction:
CH₃COOH ⇌ H⁺ + CH₃COO⁻

When an acid (H⁺) is added:

CH₃COO⁻ combines with added H⁺ to form CH₃COOH.

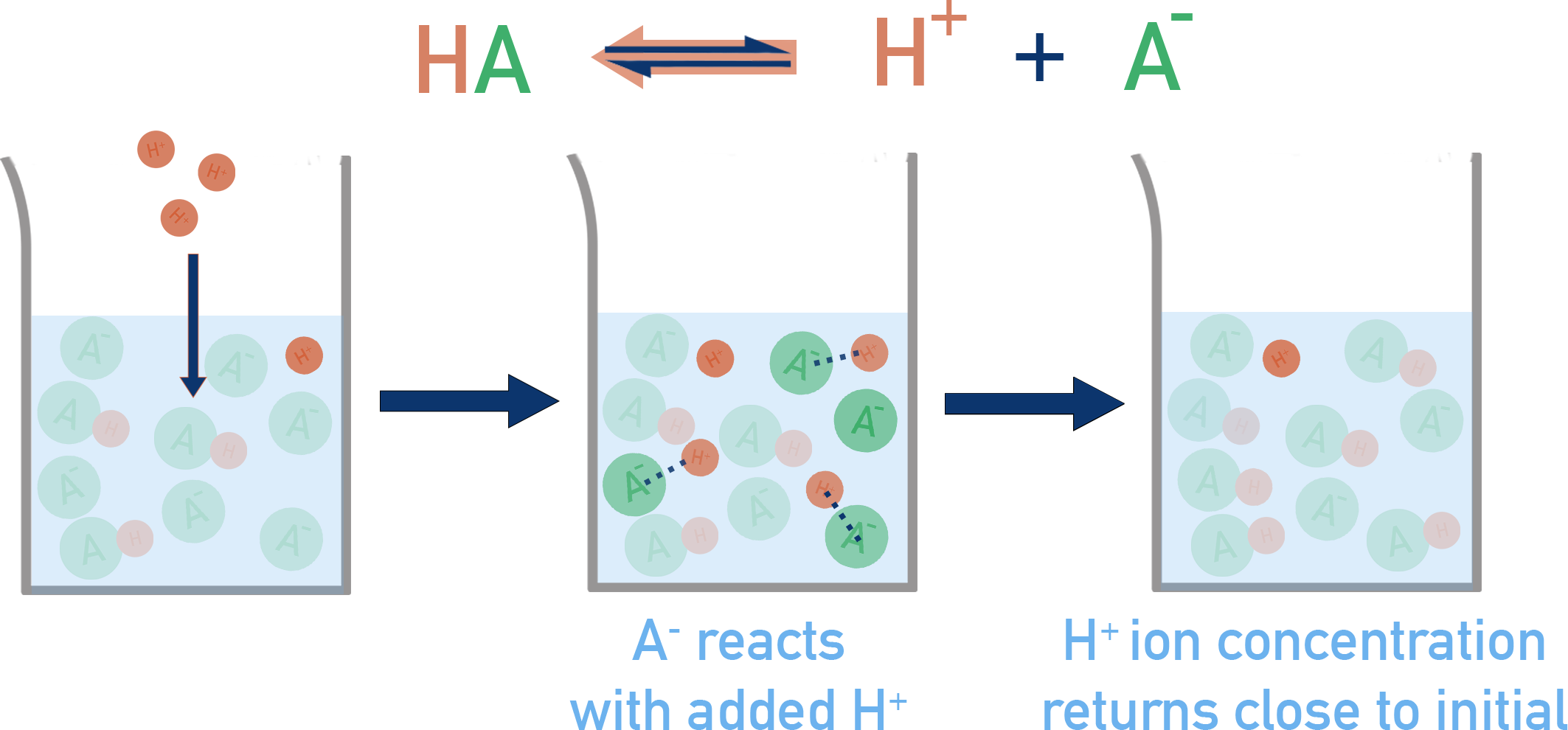
Equilibrium shifts left, reducing the increase in H⁺. [HA] increases and [A⁻] decreases.

When a base (OH⁻) is added:
The added OH⁻ reacts with H⁺ to form H₂O.
CH₃COOH dissociates more to replace lost H⁺.

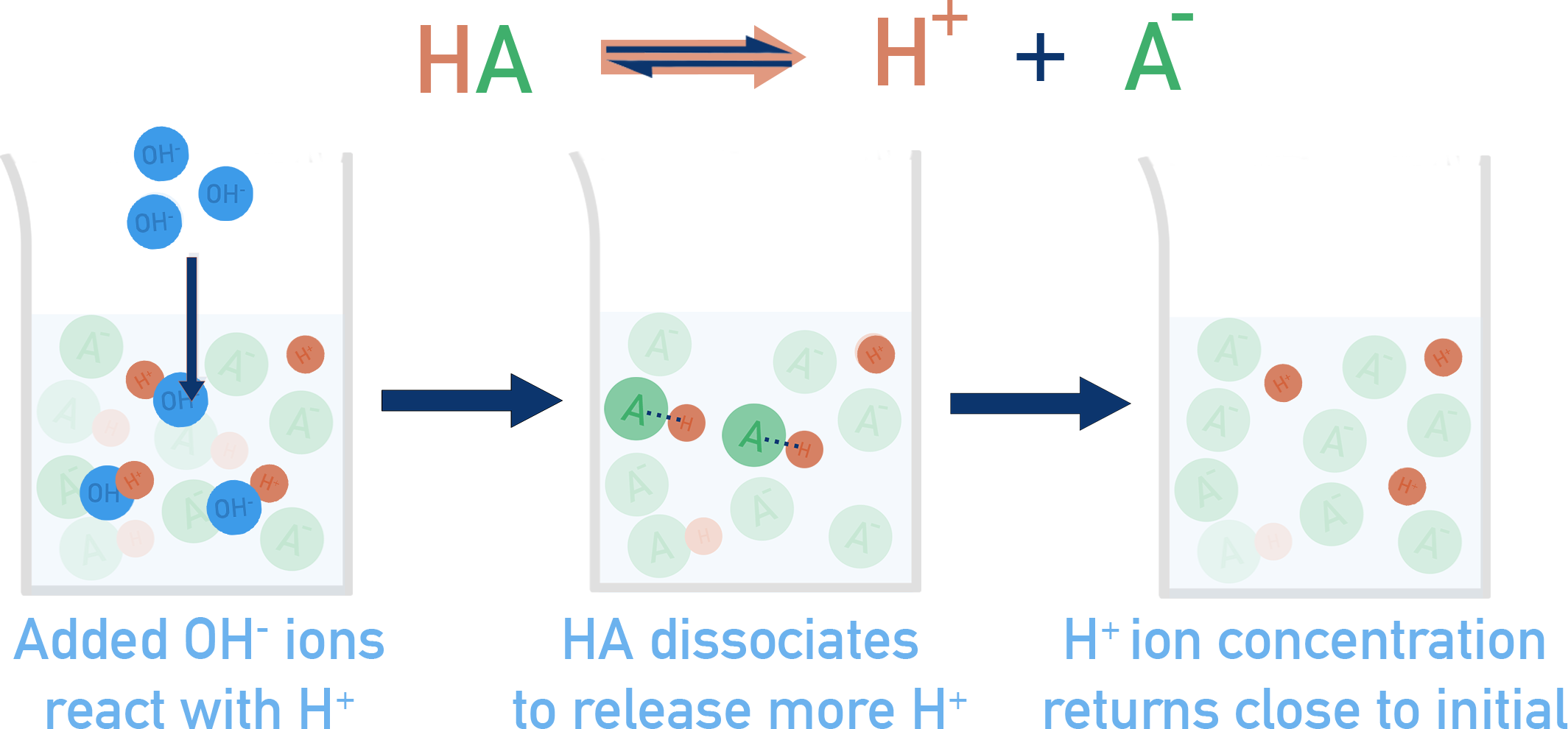
Equilibrium shifts right, replacing H⁺ ions that reacted with the added OH⁻, resisting pH increase. [HA] decreases and [A⁻] increases.

Matt’s exam tip

Remember that the concentration of HA and A^- will change when H⁺ or OH^- ions are added. When H⁺ ions are added to the mixture - the moles of HA will increase by the same as the moles of H⁺ added and moles of A^- decrease by the same amount. When OH^- ions are added - the moles of HA will decrease by the same as moles of OH^- added and the moles of A^- increase by the same amount.

Role of HCO₃⁻ in Blood Buffers

Blood pH is controlled by a hydrogencarbonate buffer system:
H₂CO₃ ⇌ H⁺ + HCO₃⁻

• If H⁺ is increased then HCO₃⁻ removes H⁺, forming H₂CO₃.
• If OH⁻ is added then H₂CO₃ releases H⁺, neutralising the OH⁻.

This maintains blood pH around 7.4.

Buffer pH Calculations

For an acidic buffer:

• Ka = [H⁺][A⁻] / [HA]
  Rearranging: [H⁺] = Ka × [HA]/[A⁻]
  Then: pH = –log[H⁺]

Note:

• For these calculations to work, we have to assume [HA] and [A⁻] are much larger than [H⁺], so their concentrations don’t change significantly.

Solubility Product, Ksp

When a sparingly soluble salt dissolves in water, an equilibrium is set up between the solid phase and the ions in solution:

A_xB_y(s) ⇌ xA⁺(aq) + yB⁻(aq)

The equilibrium constant for this process is called the Solubility Product Constant, or K_sp.

• It is not the same as solubility — instead, it represents the product of the ion concentrations at equilibrium.
• K_sp is temperature-dependent.
• Although K_sp is derived from activities and technically has no units, we often use molar concentrations in calculations.

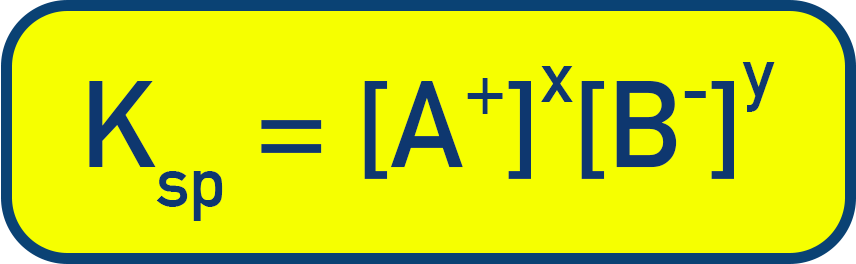
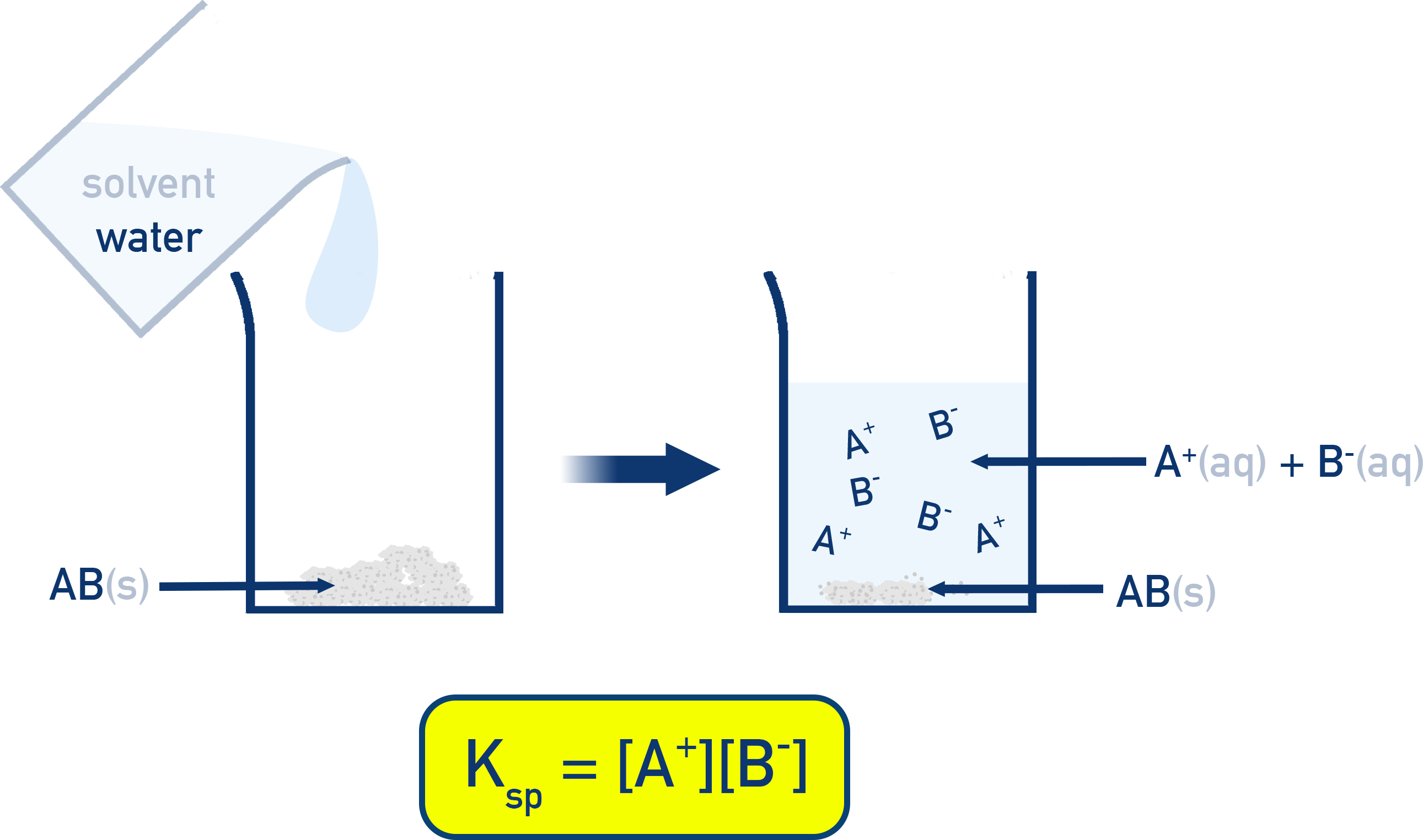
Remember solids aren’t included in equilibrium expressions.

Example: AgCl(s) ⇌ Ag⁺(aq) + Cl⁻(aq)

Ksp = [Ag⁺][Cl⁻]
A higher Ksp means greater solubility.
Ksp values change with temperature.

Writing K_sp Expressions

When writing K_sp expressions, always use ion concentrations and molar coefficients of ions in the compound's formula:

Example: Ca(OH)₂

Ca(OH)₂ ⇌ Ca²⁺ + 2OH⁻
Ksp = [Ca²⁺][OH⁻]²
(Always raise concentrations to the power of their balancing numbers.)

Calculating K_sp

Common Ion Effect and Ksp Calculations

When a solution already contains one of the ions from a dissolving salt, we call it a common ion.

Adding a common ion causes the equilibrium to shift leftward (toward the undissolved salt), according to Le Chatelier’s Principle, reducing the solubility of the salt.

Example: AgCl(s) ⇌ Ag⁺(aq) + Cl⁻(aq)

Adding NaCl increases [Cl⁻] which equilibrium shifts left. This causes more AgCl to precipitate and the solubility of AgCl decreases

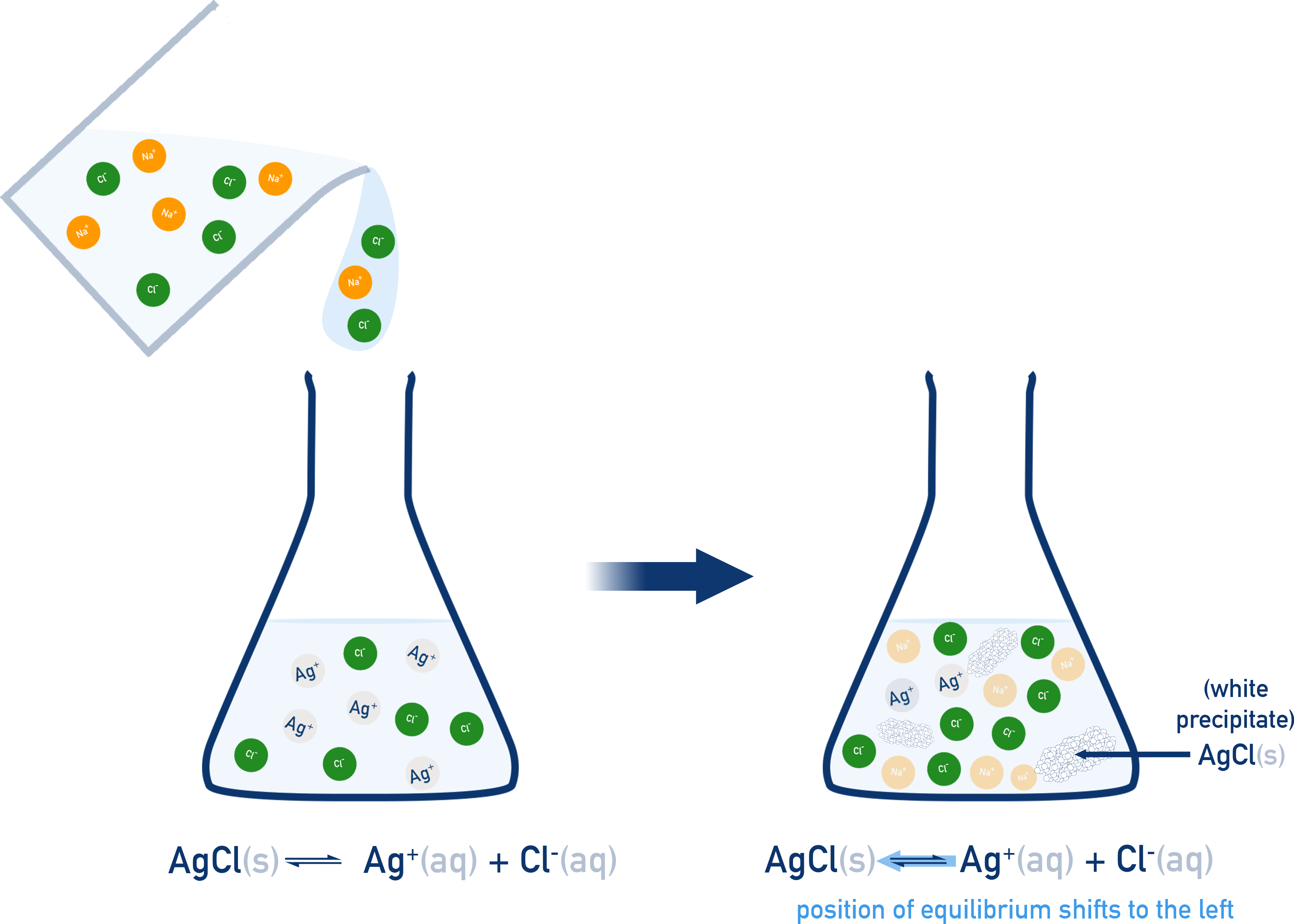
(Note: K_sp remains constant, but the concentrations adjust.)

Calculations
We can calculate the reduced solubility in the presence of common ions.

Example
Find [Ag⁺]
given K_sp of AgCl = 1.8 × 10⁻¹⁰ and [Cl⁻] = 0.10 mol dm⁻³

Let [Ag⁺] = x.
Then: Ksp = x × 0.10
Solve: x = 1.8 × 10⁻⁹ mol dm⁻³
(New solubility of Ag⁺ is very small.)

Summary

• Conjugate acid–base pairs differ by a single H⁺; identify them by tracking proton transfer.
• pH = −log[H⁺]; stronger acids have larger Ka and smaller pKa.
• Kw = [H⁺][OH⁻] (1.00 × 10⁻¹⁴ at 298 K) links acids and bases; use it to find pH of alkaline solutions.
• Buffers are made from a weak acid/base and its salt; they resist pH changes by shifting equilibrium.
• The hydrogencarbonate buffer maintains blood pH close to 7.4.
• Ksp expresses the equilibrium between a sparingly soluble solid and its ions; use it to compute solubility and common ion effects.