Colligative Properties and Determination of Molar Mass

Full Notes

When a non-volatile solute is added to a solvent, it lowers the escaping tendency of the solvent molecules, leading to changes in certain physical properties of the solution.

These properties, known as colligative properties, depend only on the number of solute particles, not their nature. As a result, they are particularly useful for experimentally determining the molar mass of solutes.

Relative Lowering of Vapour Pressure

According to Raoult's Law, the vapour pressure of a solution is lower than that of the pure solvent.

This decrease in vapour pressure depends only on the concentration of solute particles, not their identity.

The relation between vapour pressure of the solution and the mole fraction of the solvent is:

Reduction in Vapour Pressure (Δp₁):

Δp₁ = p₁⁰ − p₁ = p₁⁰ − (p₁⁰ × x₁) = p₁⁰ × (1 − x₁)

Since x₂ = 1 − x₁ (where x₂ is mole fraction of solute):

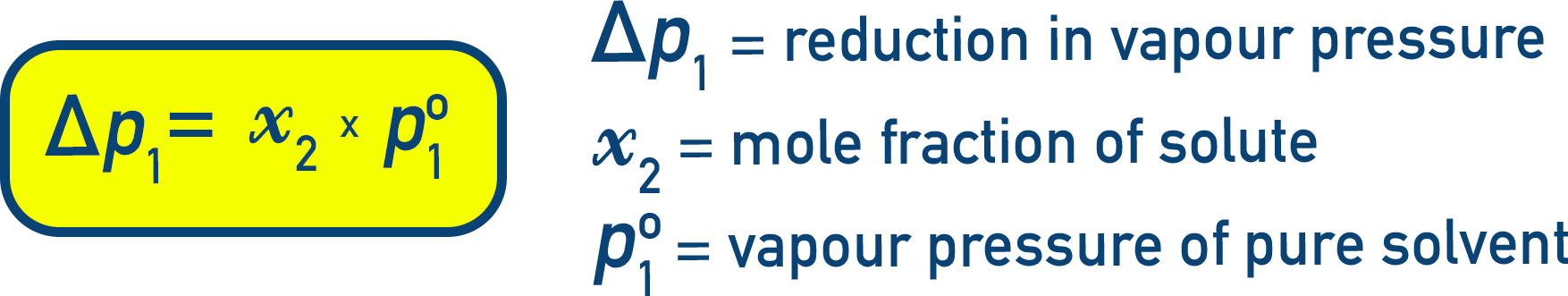
Relative Lowering of Vapour Pressure:

Dividing both sides by p₁⁰:

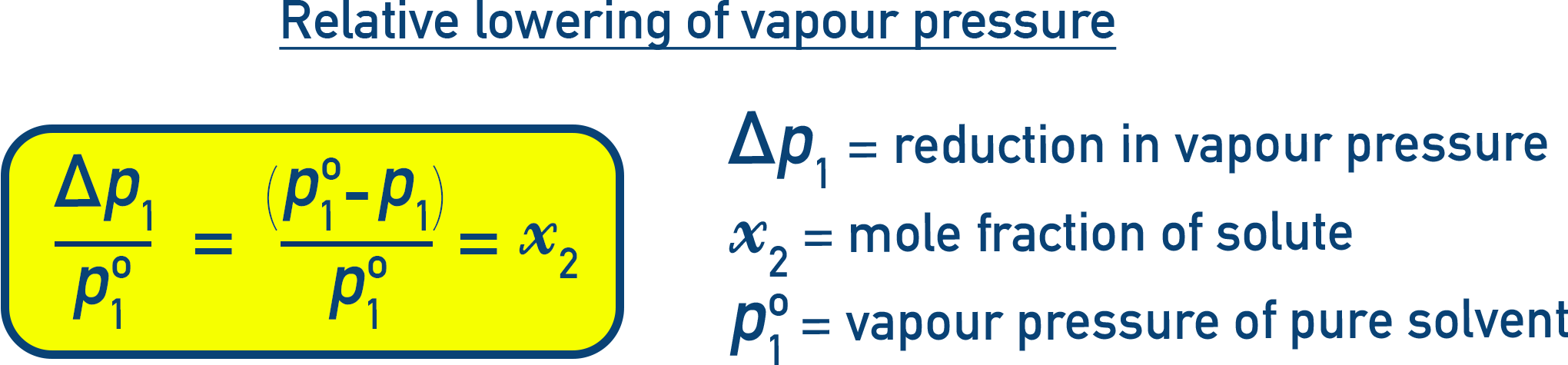
This is called relative lowering of vapour pressure, and it equals the mole fraction of the solute.

Alternate Forms:

Let n₁ = moles of solvent, n₂ = moles of solute. Then:

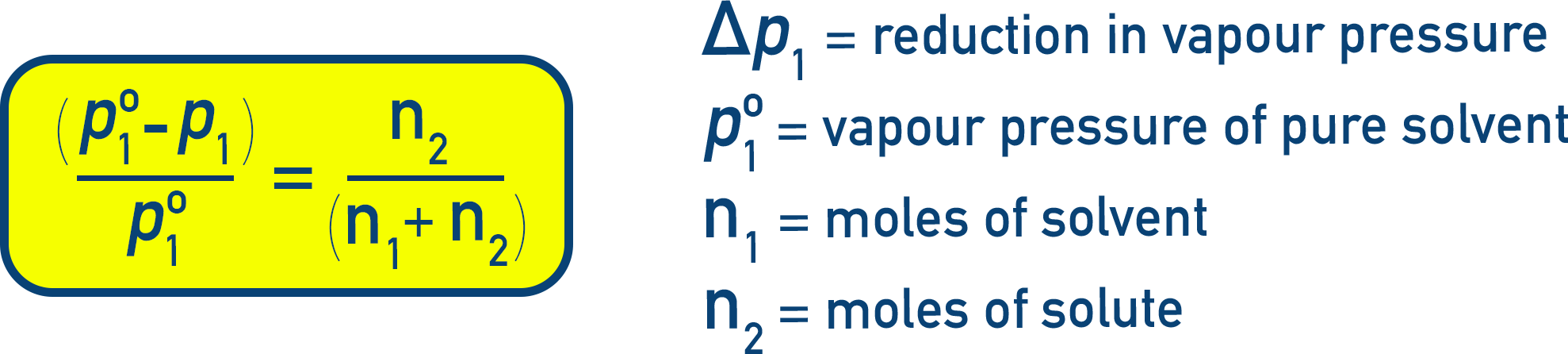
Note that for dilute solutions, n₂ ≪ n₁, meaning (n₁ + n₂) can be treated as n₁:

(p₁⁰ − p₁)/p₁⁰ ≈ n₂ / n₁

For dilute solutions we can also use masses and molar masses to replace n₁ and n₂.

Let w₁, w₂ = masses of solvent and solute respectively, and M₁, M₂ = molar masses of solvent and solute respectively. Then:

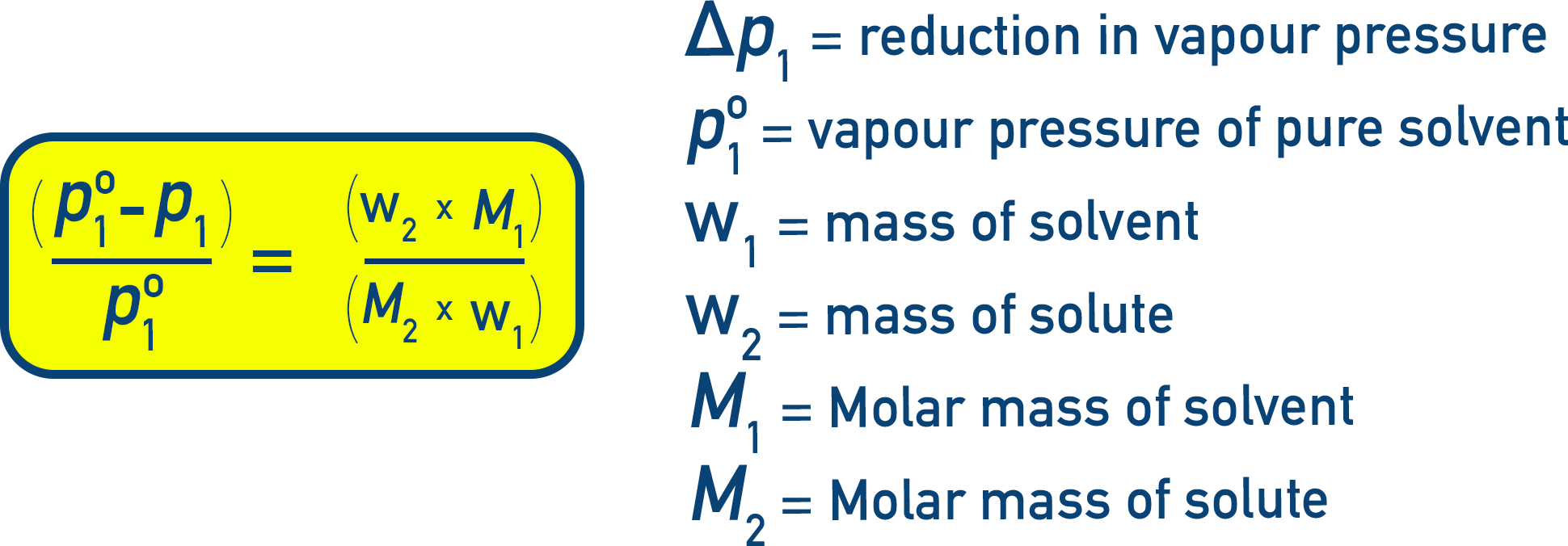
This equation can be used to calculate the molar mass of the solute (M₂), if all other quantities are known.

Elevation of Boiling Point

The presence of a solute raises the boiling point of a solvent.

The temperature at which the vapour pressure of the solution equals atmospheric pressure increases.

For example

Water boils at 373.15 K (100 °C) because its vapour pressure at this temperature is 1.013 bar (1 atm).

Effect of Non-Volatile Solute:

• When a non-volatile solute is added to a solvent the vapour pressure of the solution becomes lower than that of the pure solvent.
• Hence, to boil the solution (i.e. make vapour pressure = 1.013 bar), the temperature must be raised beyond the boiling point of the pure solvent.
• Therefore, the boiling point of the solution is higher than that of the pure solvent. This phenomenon is called Elevation of Boiling Point.

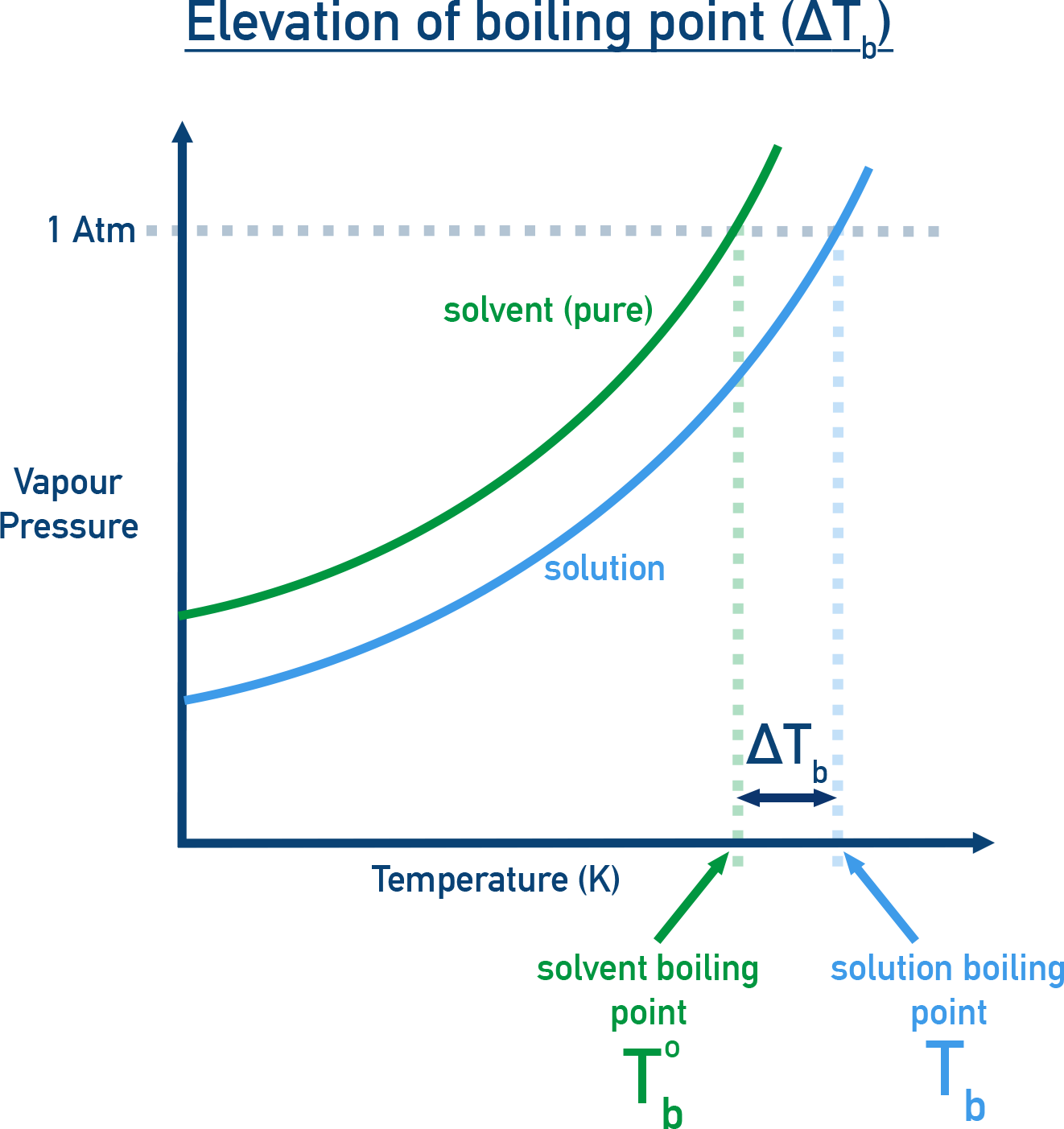
Let T_b⁰ = boiling point of pure solvent and T_b = boiling point of solution. Then,

ΔT_b = T_b − T_b⁰

This ΔT_b is called Elevation of Boiling Point.

Relation with Molality: Experiments show that for dilute solutions, elevation of boiling point is directly proportional to molality (m):

ΔT_b = K_b × m

Where K_b is the boiling point elevation constant or ebullioscopic constant with units K kg mol⁻¹.

Molality Expression (in terms of masses and molar mass):

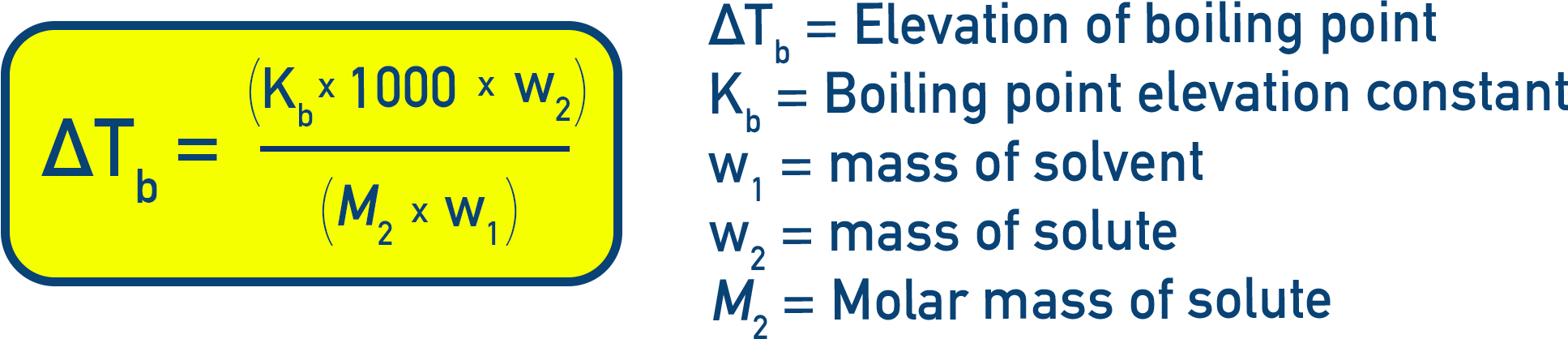
Rearranging to find molar mass (M₂):

M₂ = (1000 × w₂ × K_b) / (ΔT_b × w₁)

By measuring the boiling point elevation (ΔT_b) and knowing the quantities w₁, w₂, and K_b, we can experimentally determine the molar mass of the solute (M₂).

Depression of Freezing Point

The lowering of vapour pressure in a solution leads to a decrease in its freezing point compared to the pure solvent.

At the freezing point, the solid and liquid phases of a substance are in dynamic equilibrium.

A solution freezes when its vapour pressure equals that of the solid solvent.

When a non-volatile solute is added, the vapour pressure of the solvent decreases, so it must be cooled to a lower temperature to match the vapour pressure of the solid phase and freezing point is depressed.

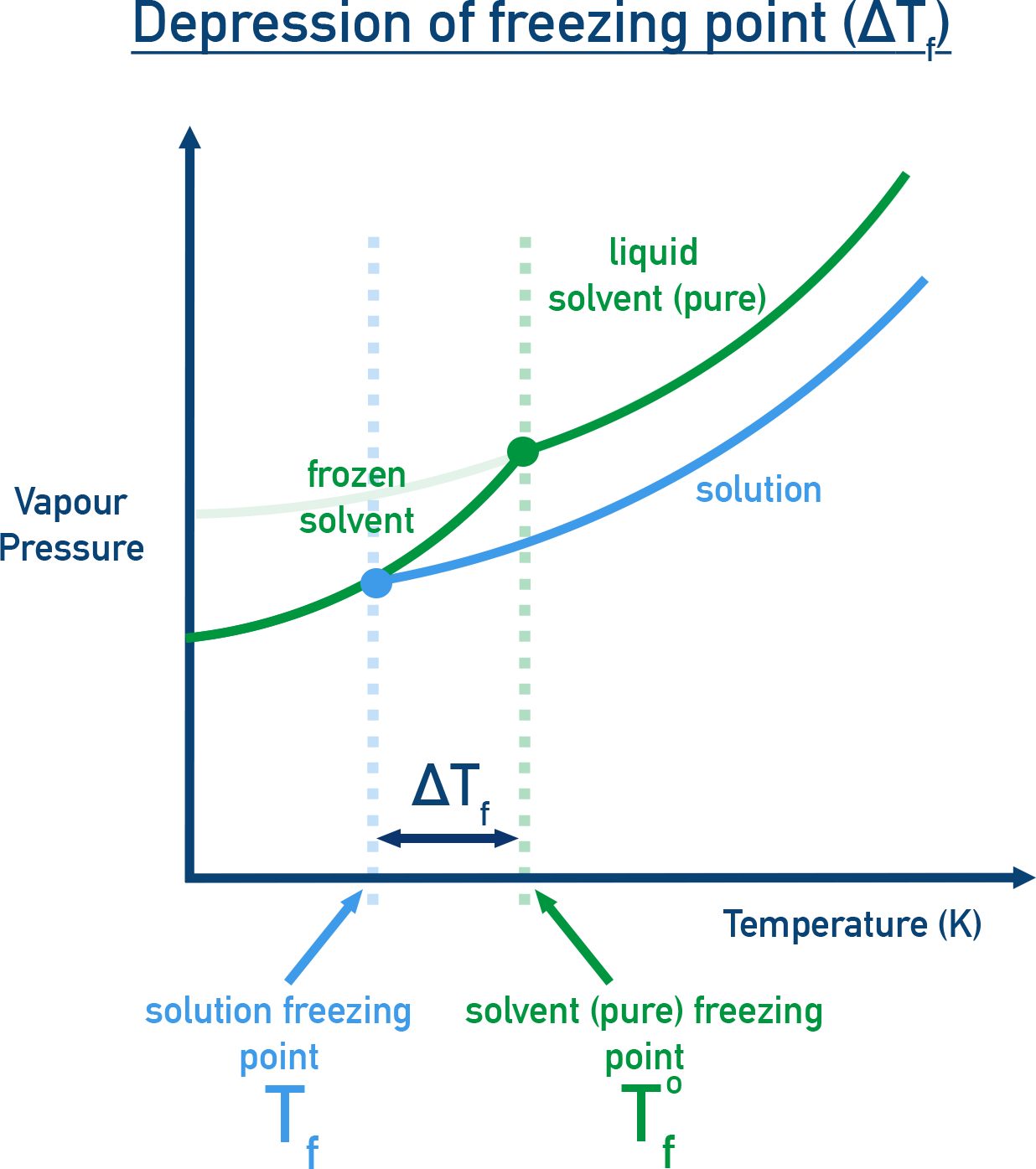
Let T_f⁰ = freezing point of pure solvent, T_f = freezing point of solution, ΔT_f = T_f⁰ − T_f = depression in freezing point.

Relationship with molality: For dilute solutions, the depression in freezing point is directly proportional to the molality (m):

ΔT_f ∝ m

ΔT_f = K_f × m

Where K_f is the freezing point depression constant (or cryoscopic constant) and m is moles of solute per kg of solvent.

Molality expression: If w₂ = mass of solute (g), M₂ = molar mass of solute, w₁ = mass of solvent (g), then

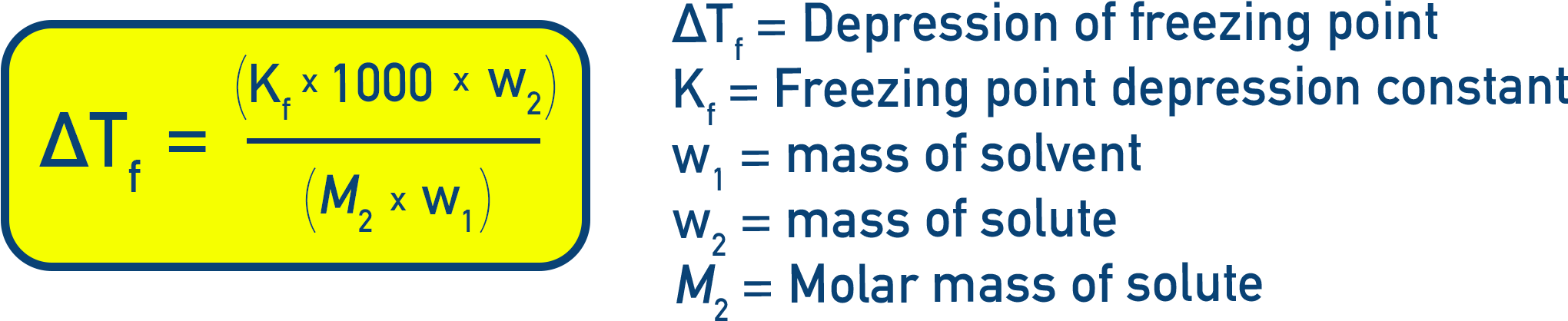
Constants and Derivations

Osmosis and Osmotic Pressure

Osmosis is the movement of solvent molecules through a semi-permeable membrane from a dilute to concentrated solution.

Solvent molecules are small enough to pass freely through the membrane, whereas solute particles are too big to pass through. Over time, there is a net movement of solvent molecules from the dilute to more concentrated solution.

Osmotic pressure (π) is the pressure needed to stop osmosis.

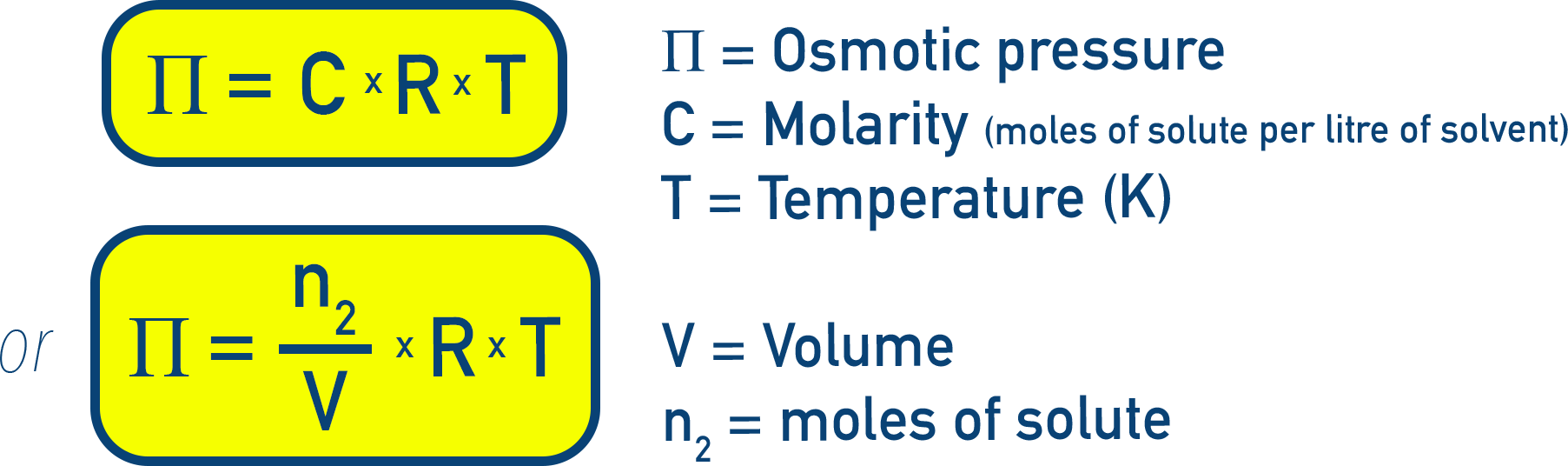
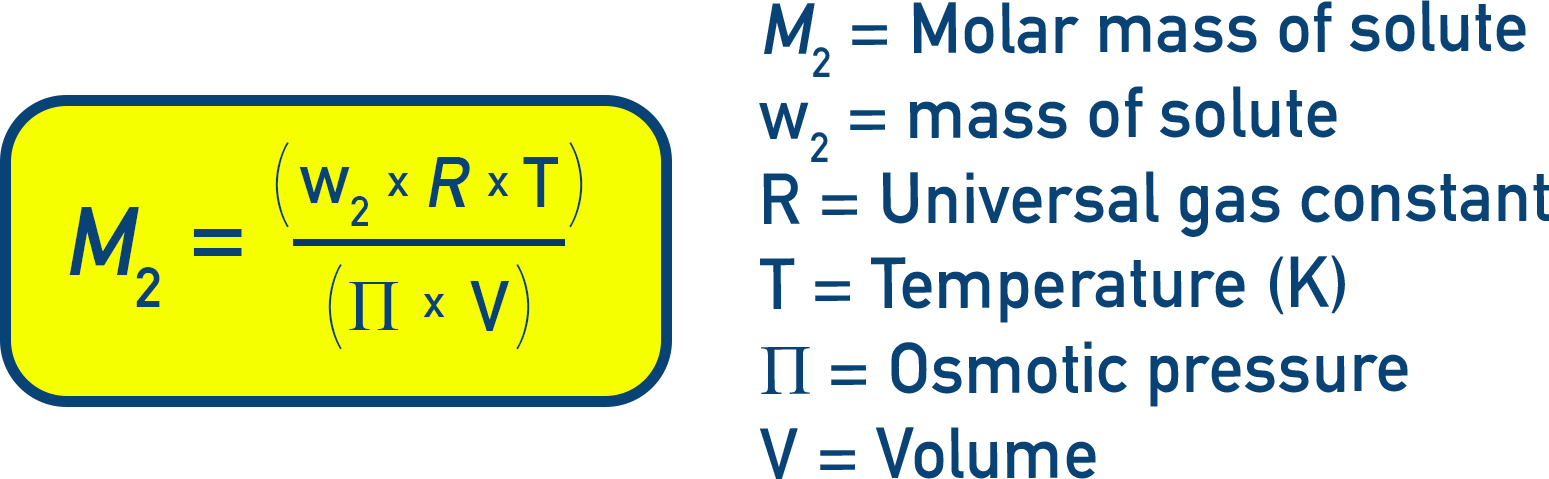
This is one of the most reliable methods for determining molar mass, especially for macromolecules like proteins or polymers.

Types of solution

Isotonic Solutions: Two solutions are called isotonic when they have the same osmotic pressure at a given temperature. If a semipermeable membrane separates them, no net osmosis occurs. For example, a 0.9% (mass/volume) sodium chloride solution has the same osmotic pressure as blood and is therefore safe for intravenous (IV) use.

Hypertonic Solution: A solution is hypertonic if its solute concentration is higher than that of the cell’s internal fluid (more than 0.9% NaCl). In such a case, water moves out of the cells, causing them to shrink.

Hypotonic Solution: A hypotonic solution has a lower solute concentration than that inside the cells (less than 0.9% NaCl). When cells are placed in a hypotonic solution, water flows into them, and they swell.

Reverse Osmosis and Water Purification

In reverse osmosis, pressure greater than osmotic pressure is applied on the concentrated side, forcing water to move from concentrated to dilute side – opposite to natural osmosis.

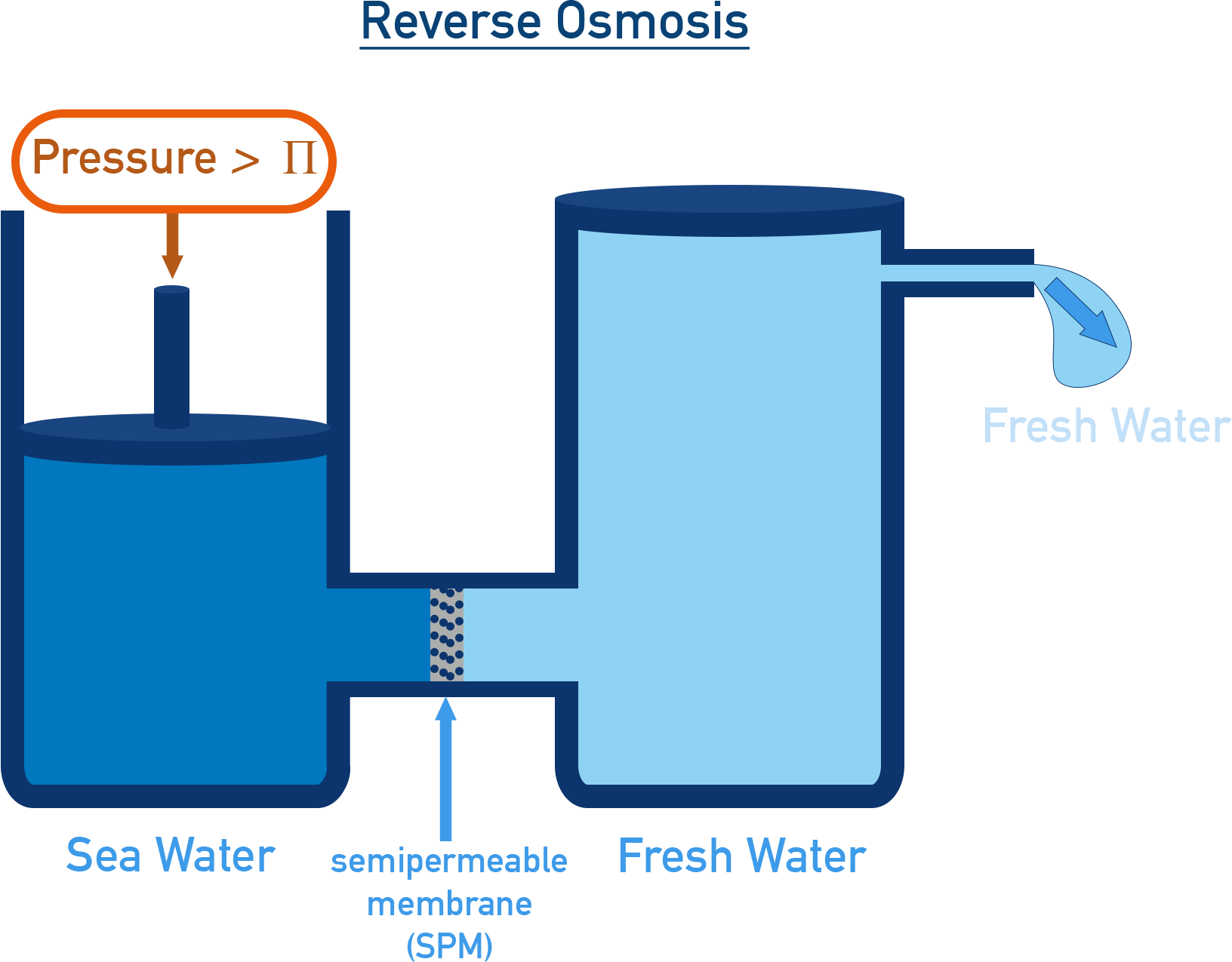
This principle is widely used in water purification (e.g., household RO filters), where pure water is extracted from saltwater or impure water.

Summary

• Colligative properties depend on the number of solute particles not their identity.
• Relative vapour pressure lowering equals the solute mole fraction in dilute solutions.
• Boiling point elevation and freezing point depression are proportional to molality.
• Osmotic pressure enables accurate molar mass measurements especially for macromolecules.
• Reverse osmosis applies pressure to drive solvent from concentrated to dilute side for purification.