Collision Theory of Chemical Reactions

Full Notes

Collision theory provides a simple and intuitive model to explain how the rate of a chemical reaction is influenced by molecular collisions. It proposes that for a reaction to proceed, reactant molecules must collide. However, not all collisions lead to a reaction—only a fraction of them are effective.

Basic Assumptions

According to the collision theory:

• Reactant molecules behave as hard spheres.
• A reaction occurs only when molecules collide.
• The number of collisions per unit time per unit volume is known as the collision frequency (Z).
• In a typical reaction, not all collisions result in product formation.

Effective Collisions and Activation Energy

For a collision to be effective:

• Molecules must have kinetic energy equal to or greater than the activation energy (E_a).
• They must also have the correct orientation for bond breaking and formation.

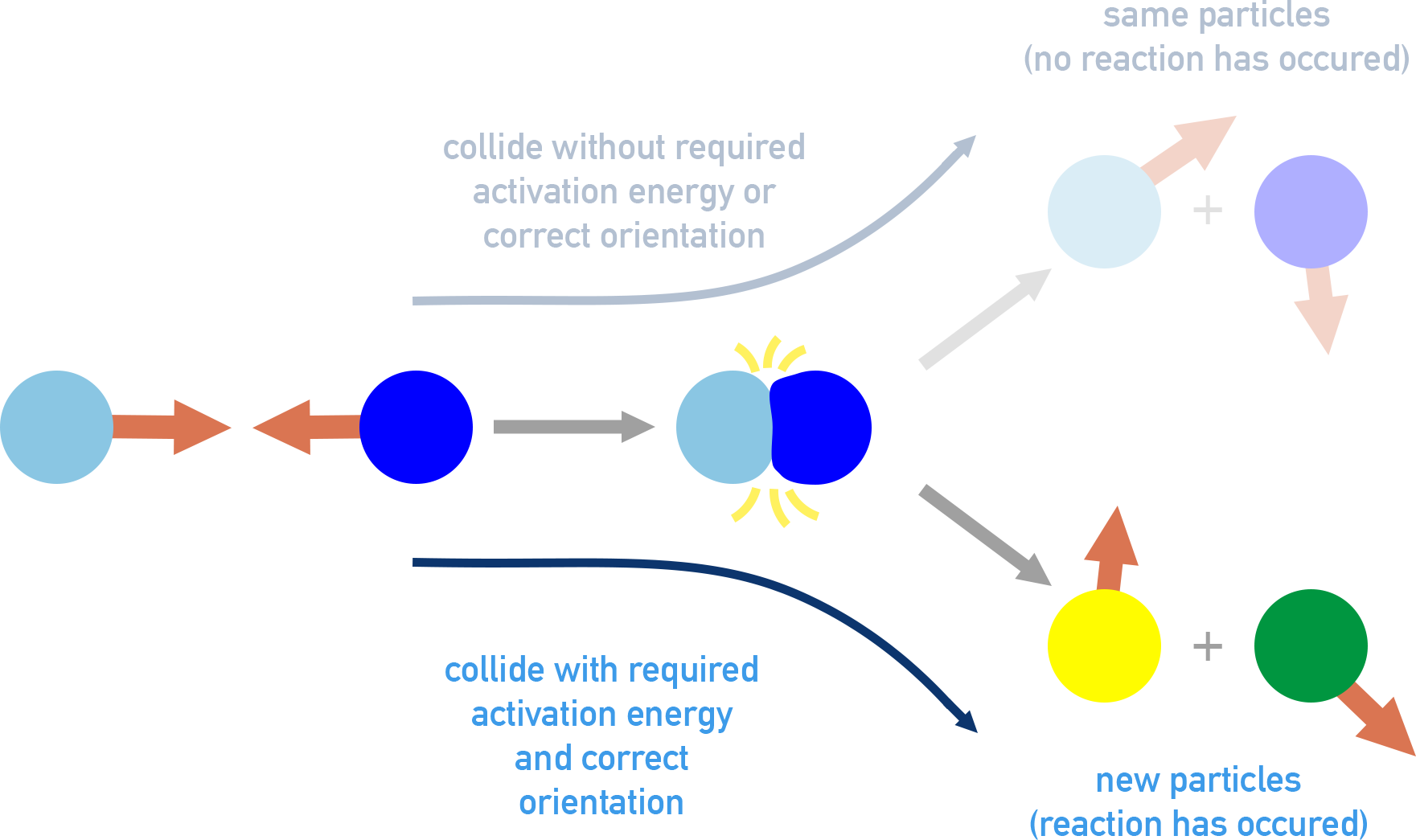
Hence, Effective collisions = collisions with correct orientation and sufficient energy.

Only a small fraction of total collisions are effective, depending on:

• Temperature
• Activation energy
• Orientation

Mathematical Expression

The fraction of effective collisions is given by the Boltzmann factor: e^−E_a/RT.

Thus, the rate of reaction is proportional to:

Steric Factor

Collision theory does not explain why even some high-energy collisions fail to result in a reaction. In order for a collision to be successful, particles have to collide with the correct orientation as well as the required activation energy.

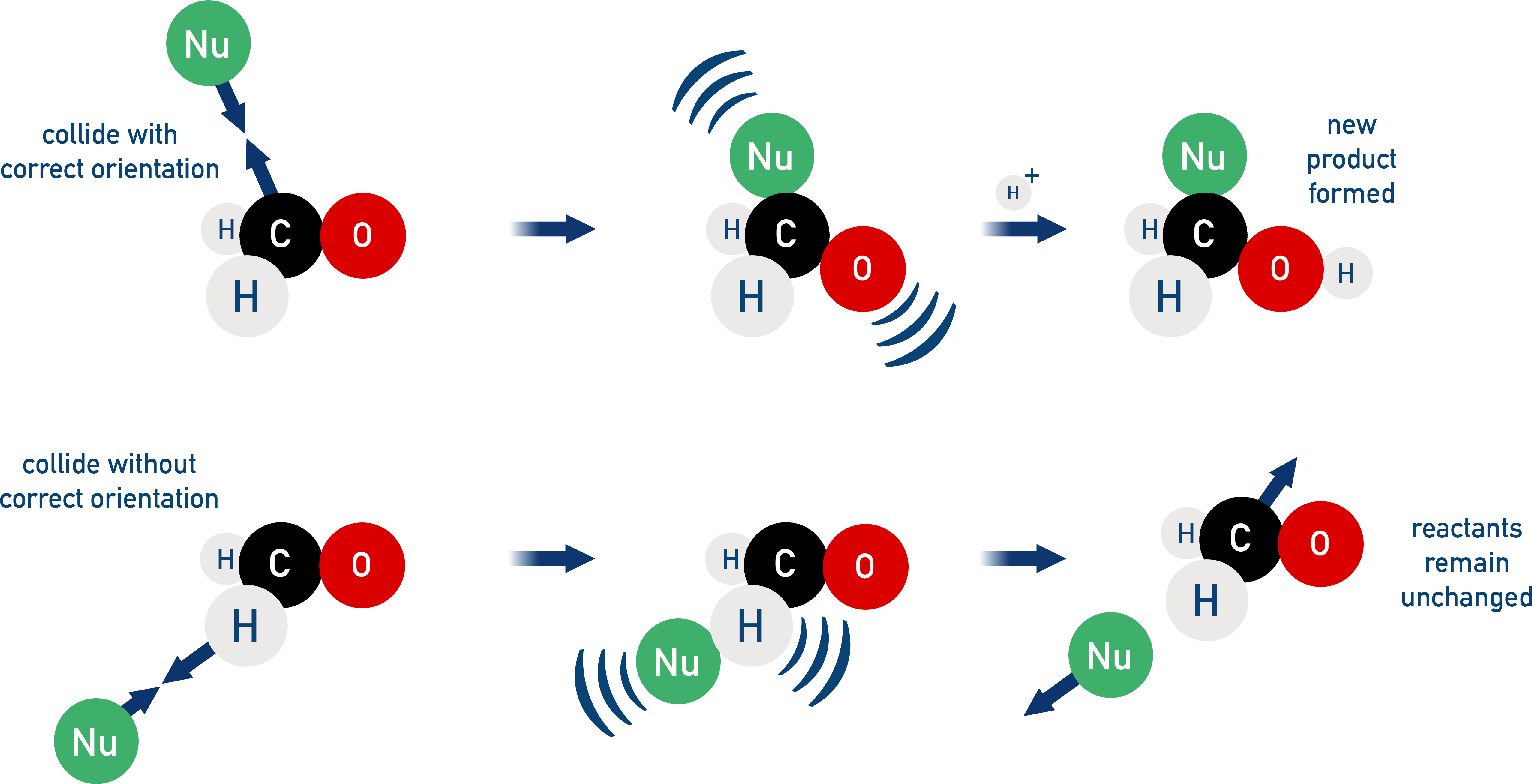
This leads to the introduction of a steric factor (P), which accounts for the orientation of reacting molecules.

The rate expression now becomes:

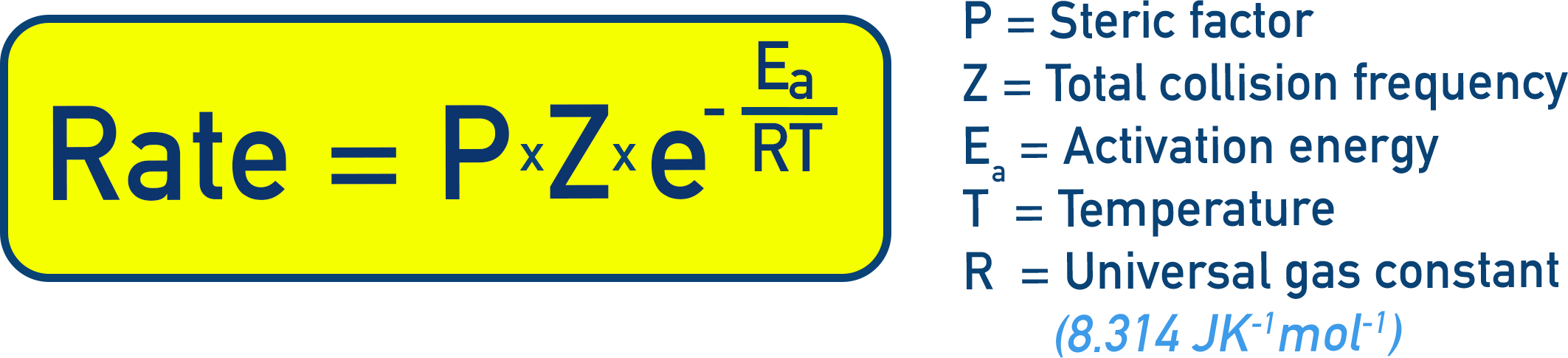
• P < 1, typically a small number.
• It varies for different reactions.
• Complex reactions may have a very low P, making them slow despite a high collision rate.

Comparison with Arrhenius Equation

The Arrhenius equation: k = A × e^−E_a/RT can be interpreted in light of collision theory:

• A includes P × Z, making it the frequency factor.
• E_a is the same activation energy.
• Both theories predict that rate increases with temperature.

Limitations of Collision Theory

• Treats molecules as hard spheres, ignoring molecular structure.
• Doesn't accurately describe reactions involving complex species.
• Inadequate in explaining slow reactions in the liquid phase, where diffusion and solvent effects are important.

Despite limitations, collision theory provides a good first approximation for gaseous reactions and offers valuable insight into kinetic behaviour.

Summary

• Only collisions with energy ≥ E_a and correct orientation are effective.
• Steric factor P accounts for orientational requirements in the rate.
• k can be written as P × Z × e^−E_a/RT aligning collision theory with Arrhenius behaviour.
• Collision theory works best for gas phase reactions and provides foundational kinetic insight.