Conductance of Electrolytic Solutions

Full Notes

Electrolytic solutions conduct electricity due to the movement of ions. Unlike metals, where electrons carry current, here the charge carriers are ions.

When voltage is applied across electrodes placed in an electrolyte, ions move to the oppositely the charged electrode, resulting in conductance.

Resistance and Conductance Basics

Resistance (R) is the property of a material that resists the flow of electric current. It is measured in ohms (Ω).

According to Ohm’s law, resistance is directly proportional to the length (l) of a conductor and inversely proportional to its cross-sectional area (A):

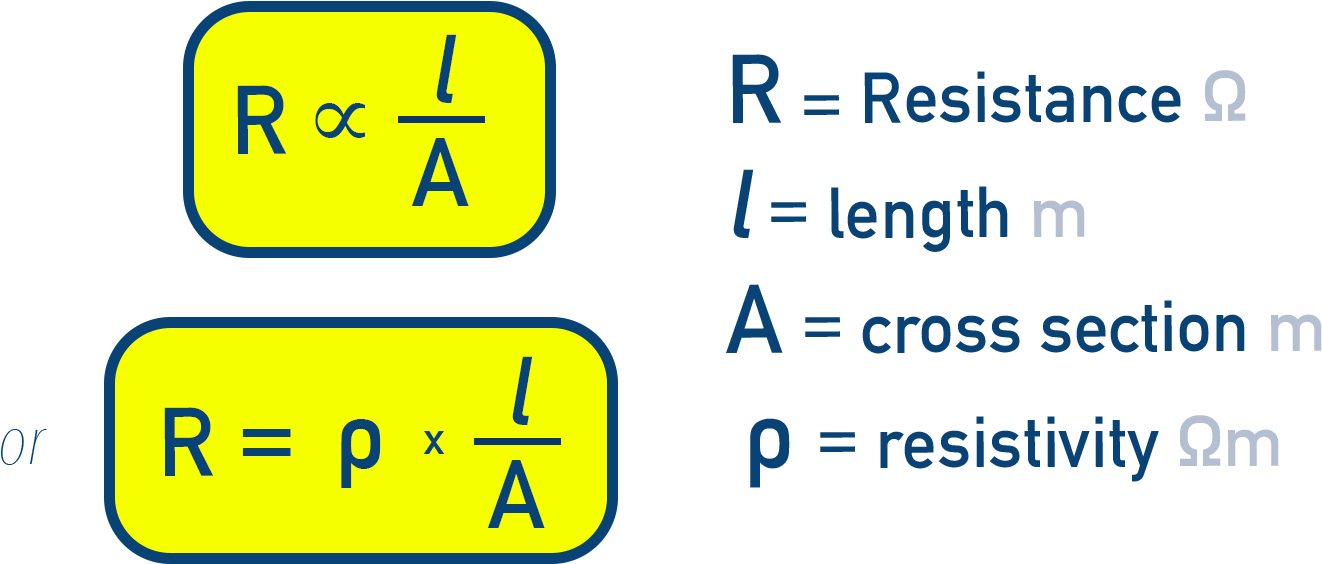
Here, ρ (rho) is the resistivity or specific resistance of the material, indicating how strongly the material opposes current flow.

The SI unit of resistivity is ohm-metre (Ω·m). However, in practice, Ω·cm is often used.

• 1 Ω·m = 100 Ω·cm
• 1 Ω·cm = 0.01 Ω·m

Conductance (G)

Conductance is the reciprocal of resistance and is a measure of how easily electricity can flow through a substance:

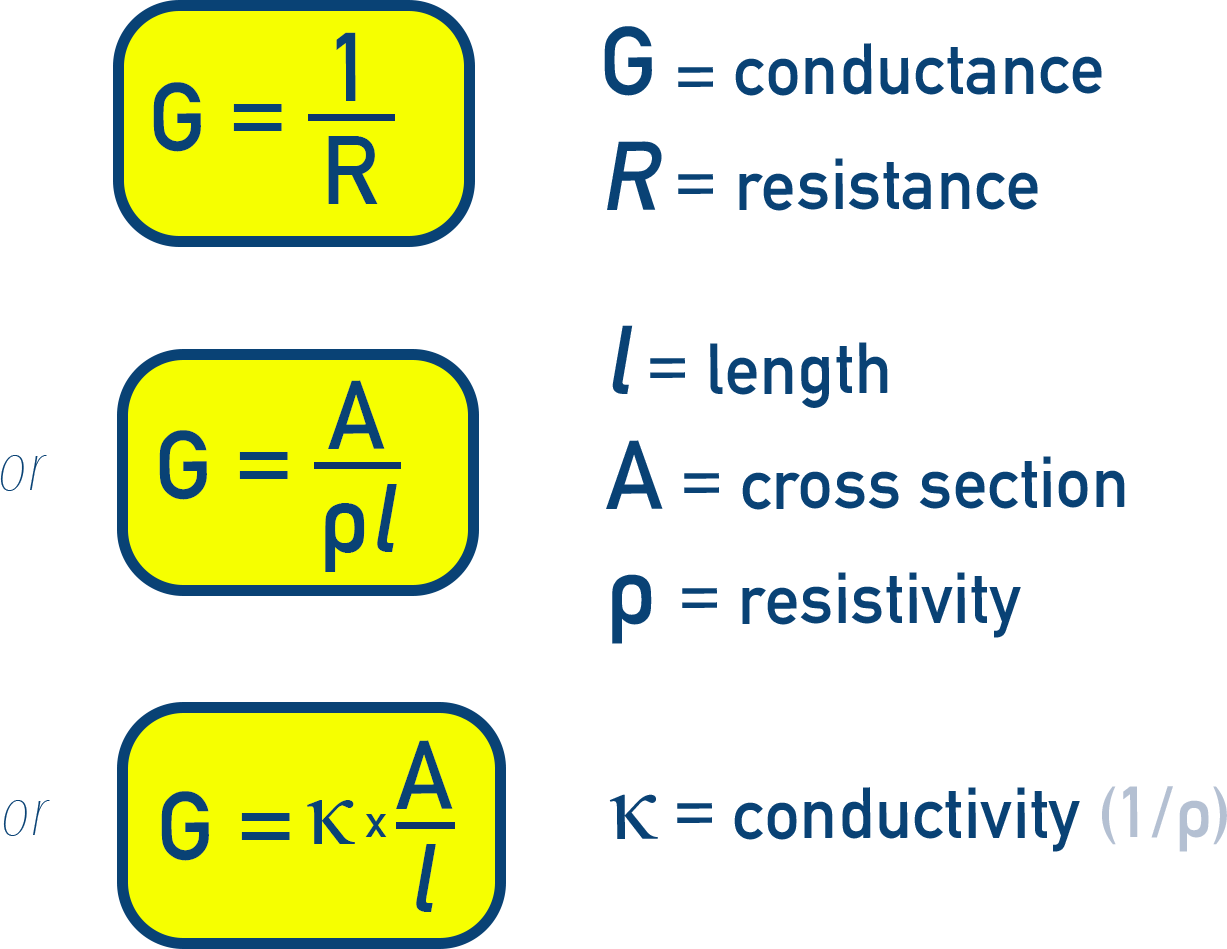
G = 1 / R

By substituting the resistance formula, conductance can also be expressed as:
G = A / (ρ × l) or using conductivity (κ): G = κ × (A / l)

Here, κ (kappa) is the specific conductance or conductivity, and it is the reciprocal of resistivity:
κ = 1 / ρ

The SI unit of conductivity is siemens per metre (S·m⁻¹). For practical use, S·cm⁻¹ is also used.

Note: 1 S·cm⁻¹ = 100 S·m⁻¹

Measurement of the Conductivity of Ionic Solutions

Different materials show a wide range of conductivities:

• Metals like copper, silver, and gold have very high conductivity.
• Insulators like glass or teflon have very low conductivity.
• Aqueous electrolyte solutions and semiconductors lie in between.

Conductance through a substance can be electronic or ionic.

Electronic Conductance

Electronic conductance is observed in metals and is due to the movement of electrons.

• The composition of the material does not change during conduction.
• Depends on:
  • The structure of the metal
  • The number of valence electrons
  • Temperature (resistance increases with temperature)

Ionic Conductance

Ionic conductance is observed in electrolytic solutions and is caused by the movement of ions.

• Depends on several factors:
  • Nature of the electrolyte
  • Size and solvation of ions
  • Type and viscosity of the solvent
  • Concentration of the electrolyte
  • Temperature (conductivity increases with temperature)

Cell Constant and Conductivity Measurement

To measure ionic conductivity, a special device called a conductivity cell is used.

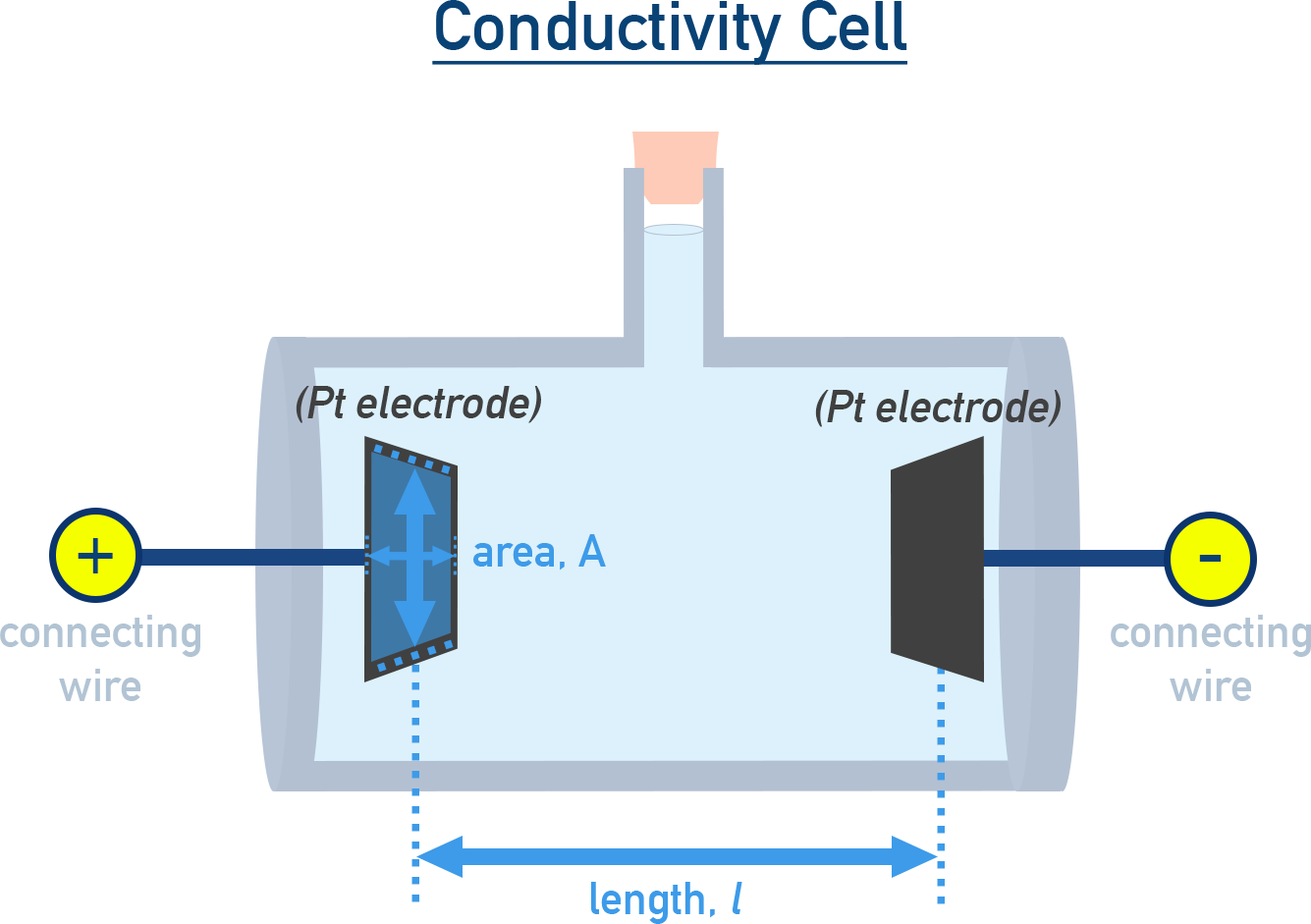
Its geometry is expressed using the cell constant (G*), given by:

The cell constant is typically determined using standard KCl solutions with known conductivity.

Once the resistance (R) is measured using a Wheatstone bridge or conductivity meter, conductivity is calculated as:

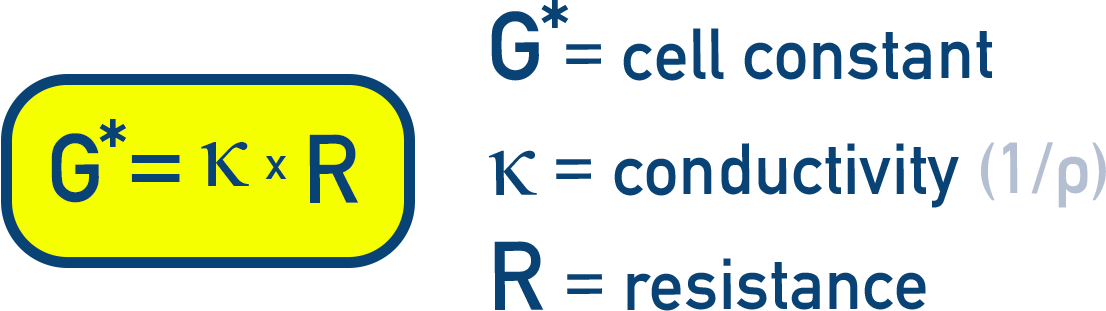
Molar Conductivity (Λ_m)

Molar conductivity is defined as the conductivity (κ) of a solution divided by its molar concentration (c):

Note — unit conversion

• If κ is in S·cm⁻¹ and c is in mol·L⁻¹, then Λ_m (S cm² mol⁻¹) is: Λ_m = (κ × 1000) / c
• 1 S·m²·mol⁻¹ = 10⁴ S·cm²·mol⁻¹
• 1 S·cm²·mol⁻¹ = 10⁻⁴ S·m²·mol⁻¹

Variation of Conductivity and Molar Conductivity with Concentration

Conductivity (κ)

• As the solution is diluted, its conductivity decreases. This is because the number of ions per unit volume drops, leading to fewer charge carriers and thus lower conductivity.
• This applies to both strong and weak electrolytes.

Molar Conductivity (Λ_m)

• Molar conductivity increases with dilution. As the solution becomes more dilute:
  • The ions become more separated.
  • Interionic interactions reduce.
  • In weak electrolytes, ionization increases, contributing more free ions.

Limiting Molar Conductivity (Λ_m⁰)

At infinite dilution, the molar conductivity reaches a constant value where each ion contributes independently to conductivity. This is known as limiting molar conductivity (Λ_m⁰).

Strong Electrolytes

For strong electrolytes, molar conductivity increases slightly with dilution. The relationship is often expressed as:

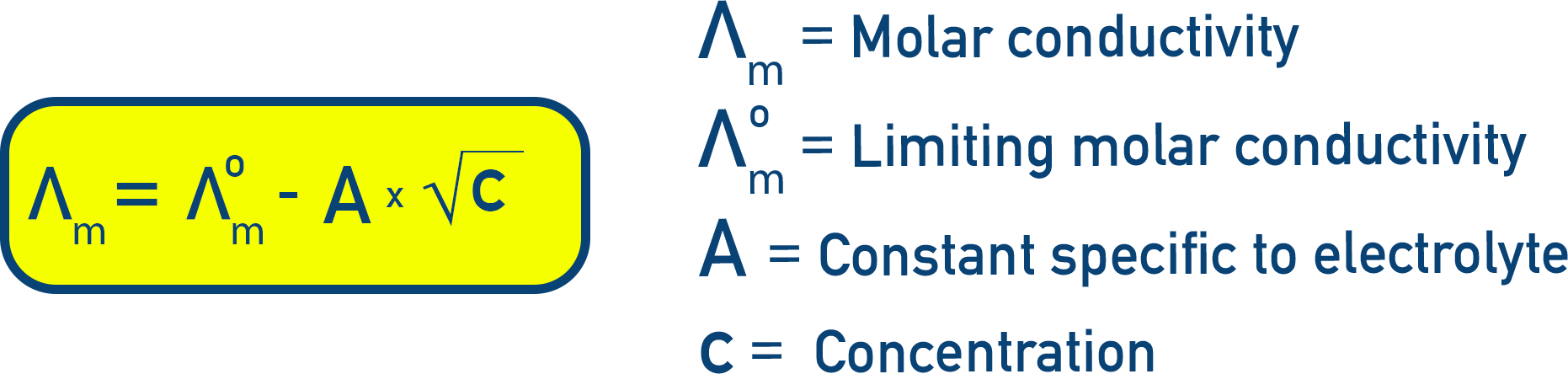
A plot of Λ_m vs √c gives a straight line.

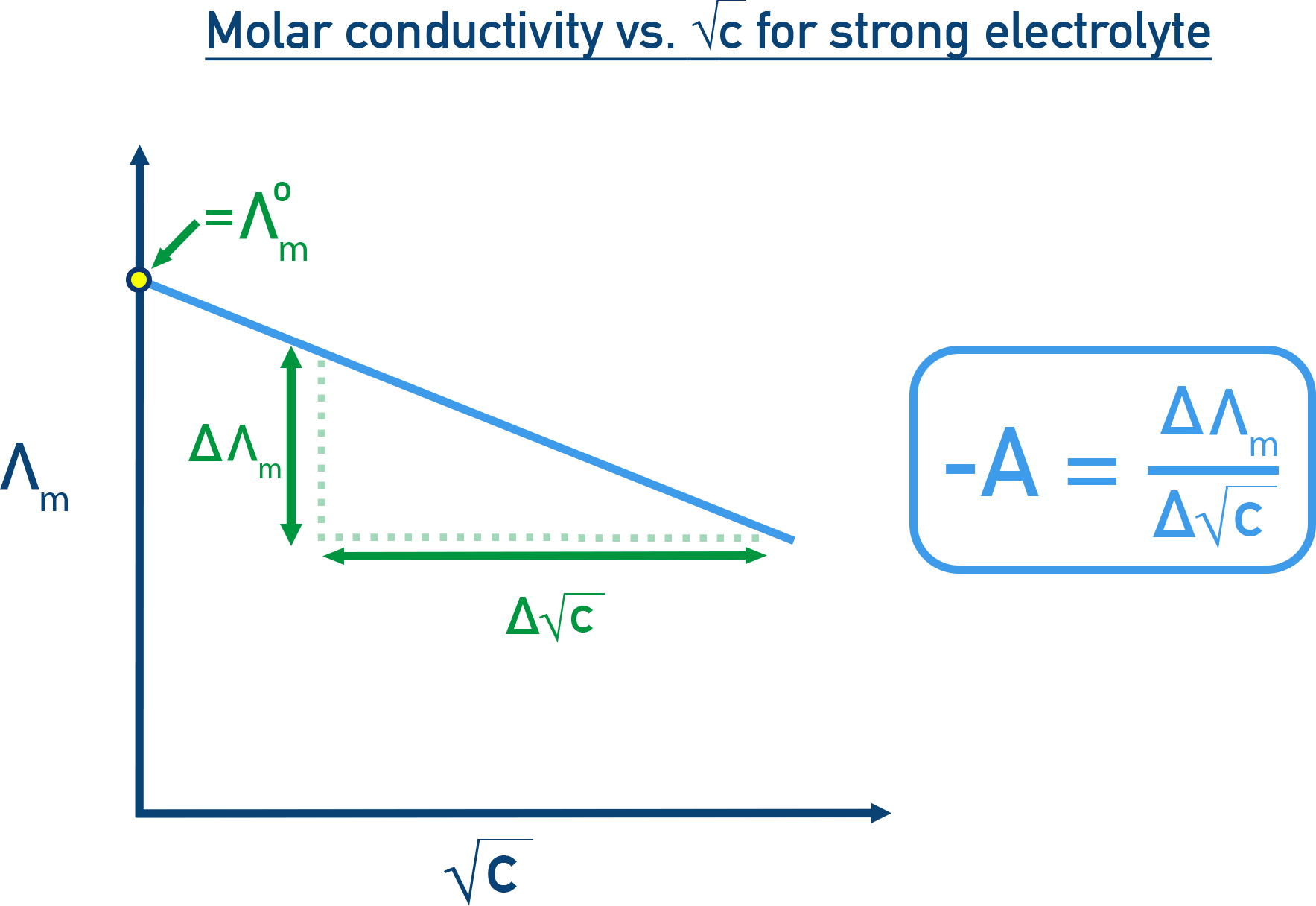
with the y intercept being Λ_m⁰ and the gradient of the line −A.

Weak Electrolytes

For weak electrolytes, molar conductivity increases sharply on dilution because more of the substance ionizes.

Λ_m⁰ cannot be found by extrapolation like strong electrolytes. Instead, it is calculated using Kohlrausch’s Law.

Kohlrausch’s Law of Independent Migration of Ions

Degree of Dissociation (α) for Weak Electrolytes

The degree of dissociation (α) is the fraction of molecules that ionize in solution and is calculated using:

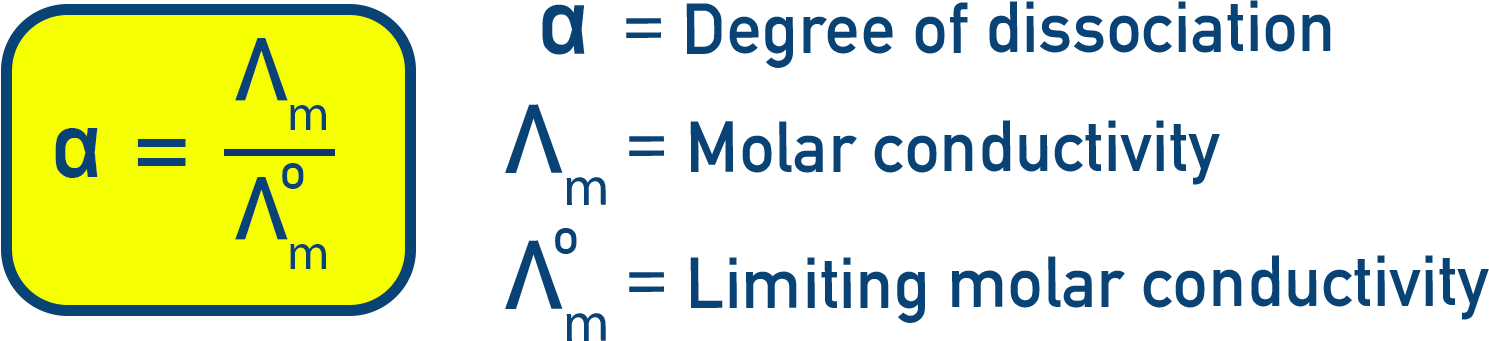
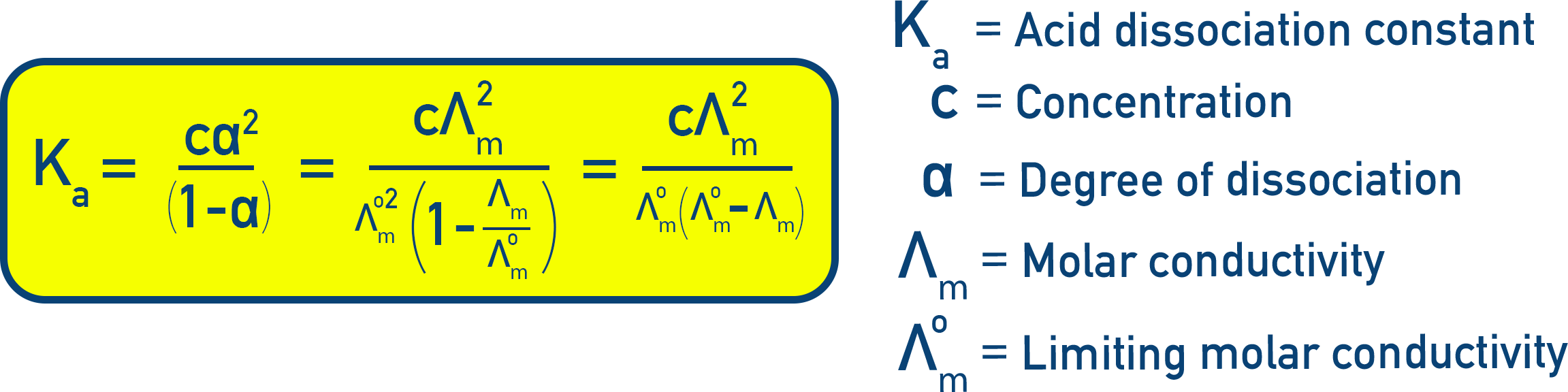
Dissociation Constant (K_a)

The acid dissociation constant for a weak electrolyte (see Class 11, topic 6.9) can be determined using:
K_a = (c × α²) / (1 − α)

Substituting α gives:

Applications of Kohlrausch’s Law

• It helps determine the Λ_m⁰ for weak electrolytes that cannot be measured directly.
• Using Λ_m⁰, one can calculate the degree of dissociation (α) and the acid dissociation constant (K_a) for weak acids like acetic acid.

Summary

• Conductivity arises from ion motion in electrolytes and depends on concentration and temperature.
• Molar conductivity increases with dilution and reaches Λ_m⁰ at infinite dilution.
• Strong electrolytes show Λ_m vs √c linearity while weak electrolytes require Kohlrausch’s Law.
• Cell constant enables conversion of measured resistance to κ for quantitative analysis.