Temperature Dependence of the Rate of a Reaction

Full Notes

The Temperature–Rate Link

Chemical reactions occur when molecules collide with sufficient energy and proper orientation. Not all collisions lead to a reaction – only those that overcome an energy barrier known as activation energy (E_a) are successful.

Maxwell-Boltzmann Distribution curves show the distribution of kinetic energies in a sample of particles at a given temperature.

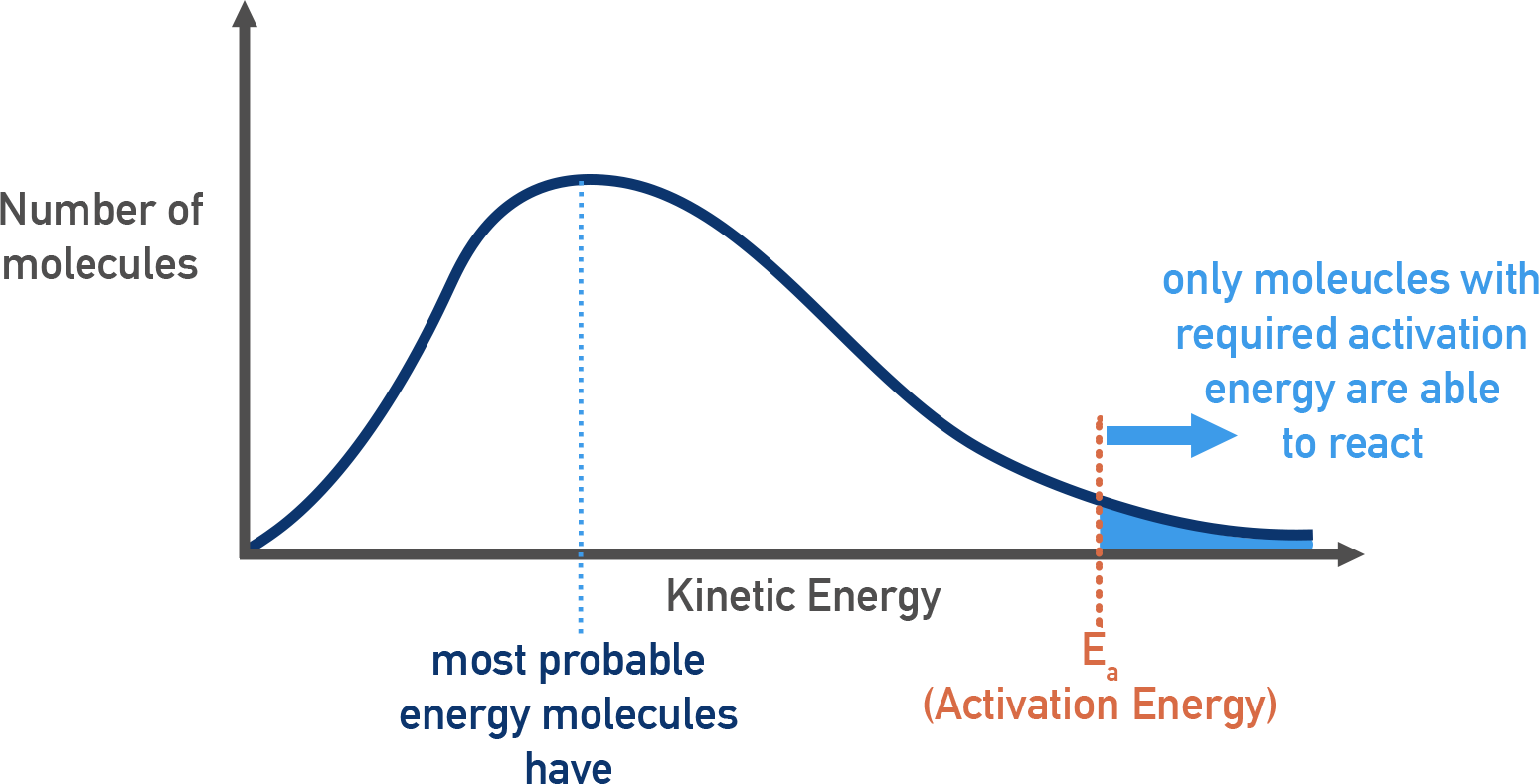
• Most particles have moderate energy
• A few have high enough energy to react
• The area under the curve beyond the activation energy (E_a) represents the fraction of particles that can successfully react

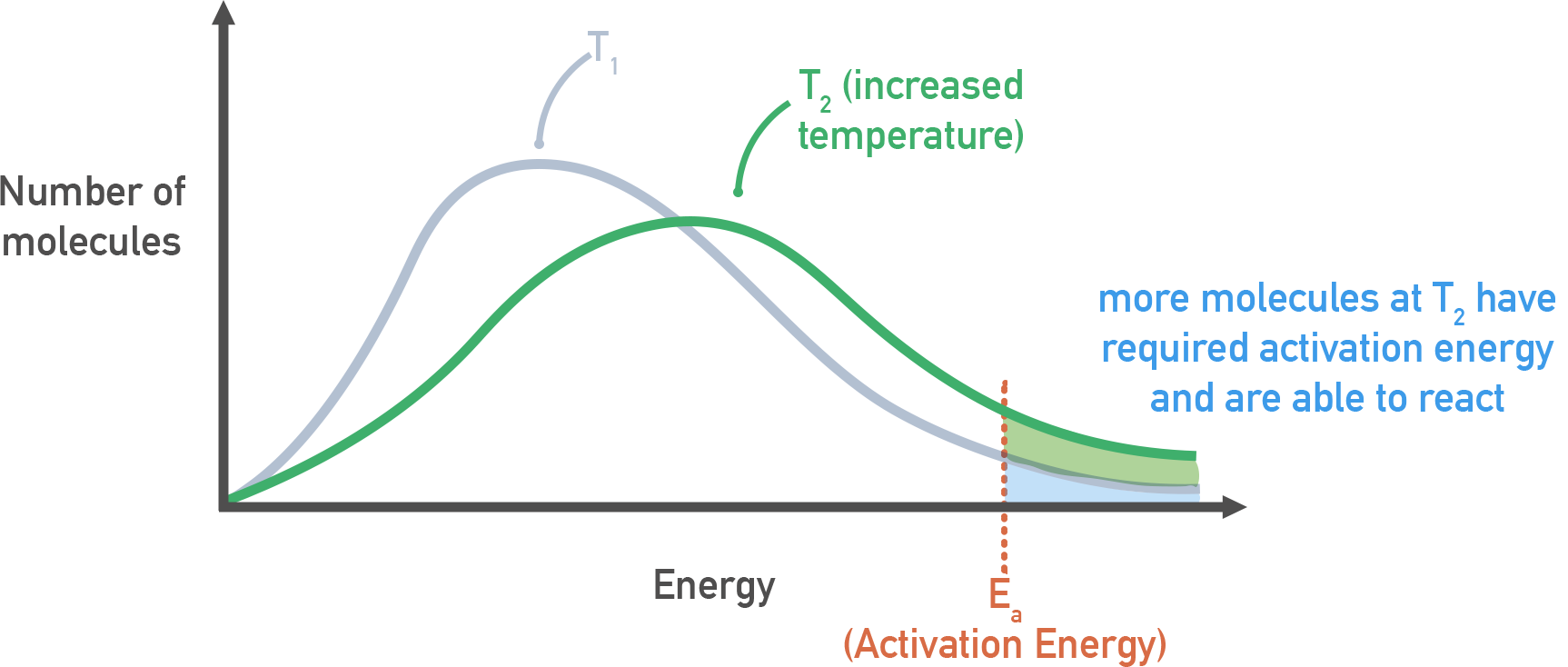
As temperature increases, a greater proportion of molecules have sufficient energy to cross this barrier, leading to an increase in the rate of reaction.

The Arrhenius Equation

The Arrhenius equation, proposed by Svante Arrhenius, gives a quantitative relationship between the rate constant of a reaction and temperature, accounting for the fraction of molecules that can overcome the activation barrier.

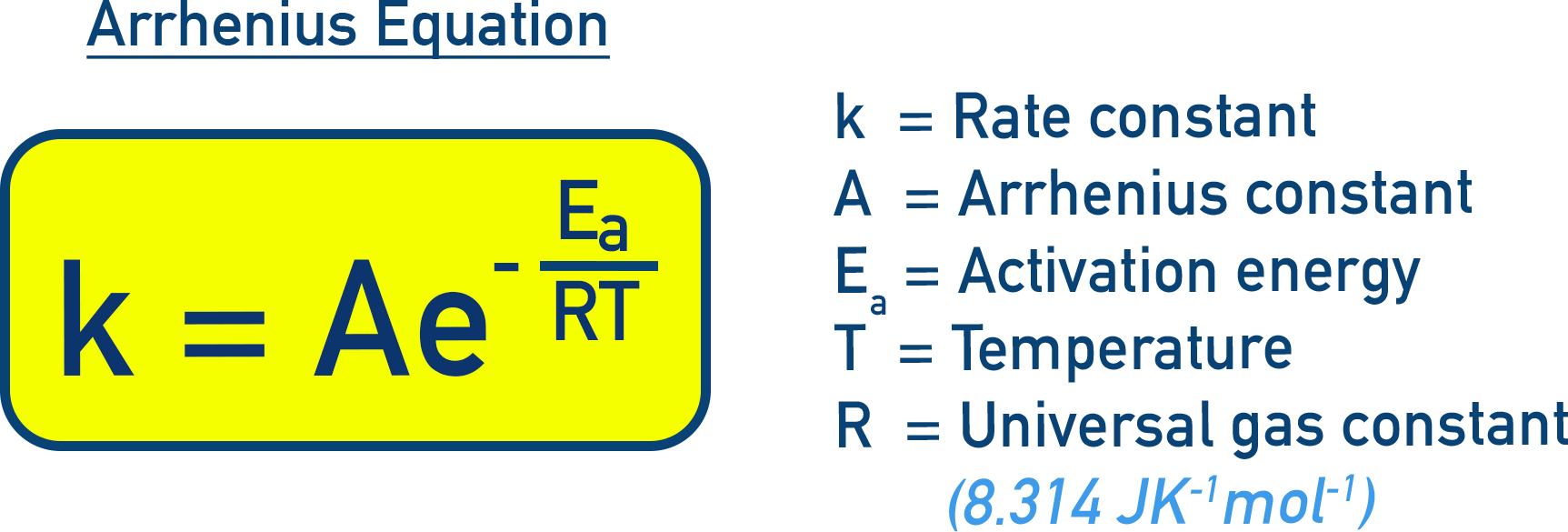
As T increases, the negative exponent (−E_a/RT) becomes less negative, so e^−E_a/RT increases and rate constant k increases = reaction proceeds faster.

Interpretation

• A (frequency factor): Reflects how often molecules collide in the correct orientation.
• E_a (activation energy): Minimum energy required for a successful collision.
• e^−E_a/RT: Fraction of molecules with energy ≥ E_a at a given T.

Even small increases in temperature cause large increases in k, due to the exponential component of the equation.

Logarithmic Form of the Arrhenius Equation

To make the Arrhenius equation easier to work with, we can take natural logs on both sides:

This linear equation (y = mx + c) allows for graphical determination of E_a:

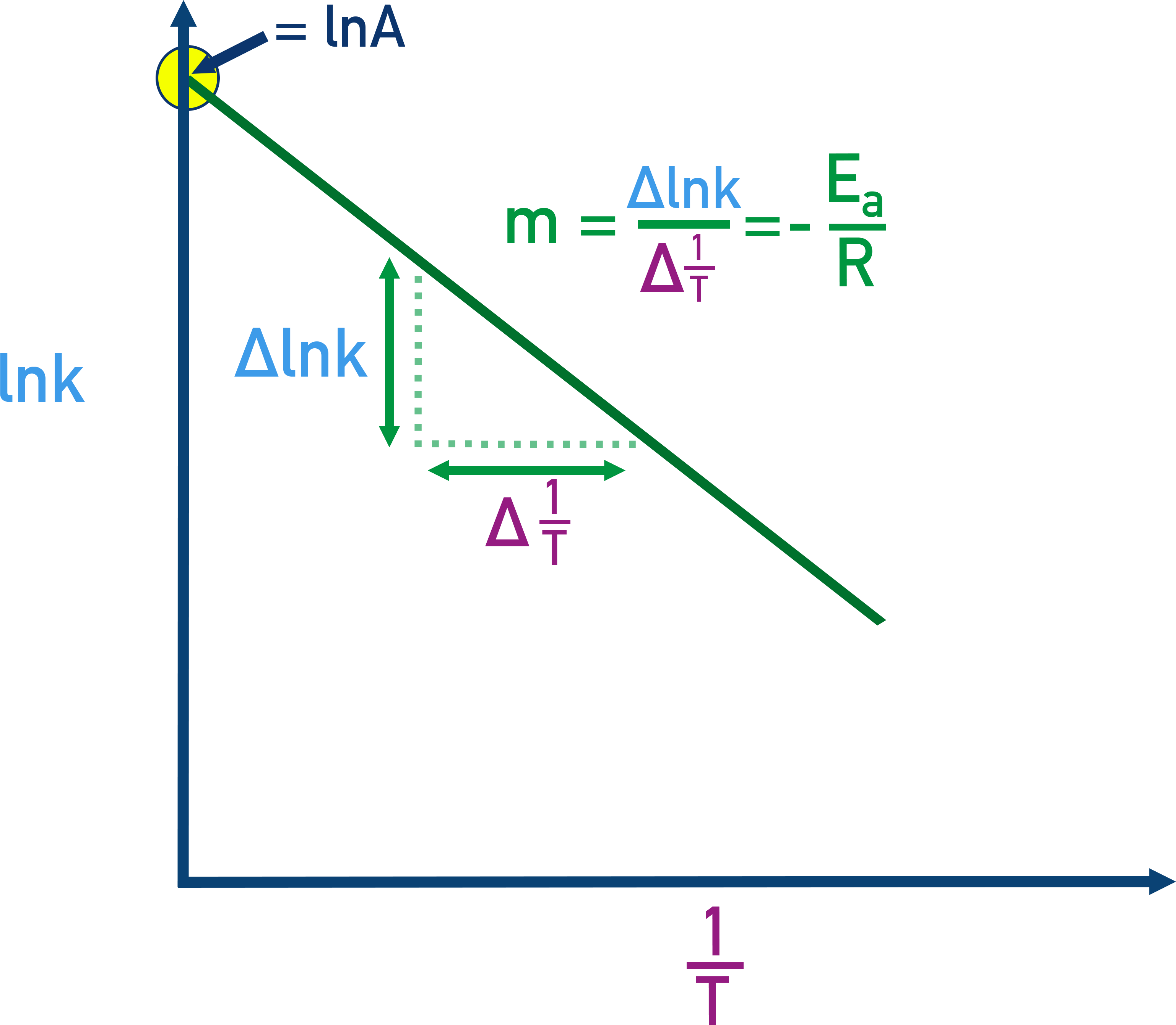
• Plot of ln k vs 1/T is a straight line.
• Slope = −E_a/R → gives activation energy.
• Intercept = ln A

This is useful for analysing experimental data to determine E_a or A.

Two-Temperature Form

To compare rate constants at two different temperatures:

ln(k₂/k₁) = (E_a/R) × ((T₁ − T₂)/(T₁T₂))

where

• k₁ and k₂ are rate constants at temperatures T₁ and T₂ (in K)
• Allows us to predict how much the rate will change with temperature
• Alternatively, it can be used to calculate E_a using experimental data.

Effect of Catalyst

A catalyst is a substance that increases the rate of a chemical reaction by providing an alternative pathway with lower activation energy (E_a).

• Catalyst does not alter the equilibrium or final enthalpy change (ΔH).
• It only affects the kinetics by lowering E_a, making it easier for molecules to react.

• The energy profile of a catalysed reaction has a lower peak than the uncatalysed one.
• More molecules now possess sufficient energy (at the same temperature) to overcome the lowered energy barrier.

Summary

• Arrhenius equation explains the temperature dependence of reaction rates.
• Higher temperature leads to larger k and faster rate.
• A catalyst lowers E_a and increases the fraction of effective collisions.
• Arrhenius plots of ln k versus 1/T allow E_a and A to be obtained.