Integrated Rate Equations

Full Notes

The change in concentration of reactants with time is described by the differential rate equation. However, determining the instantaneous rate directly from experiments is often difficult because it involves calculating the slope of the tangent at a specific time on a concentration vs. time graph. This makes it hard to determine the rate law and the order of a reaction.

To overcome this, we use integrated rate equations. These equations are derived by integrating the differential rate law, giving a direct relationship between concentration, time, and the rate constant. This approach uses easily measurable data and simplifies analysis.

Different reaction orders have different integrated forms. In this section, we focus on the integrated rate laws for zero-order and first-order reactions.

Zero Order Reactions

Rate Law

The rate of a zero order reaction does not depend on the concentration of the reactant:

Rate = −d[R]/dt = k

A graph Plot of [A] vs. time is linear with slope = −k

Rate is independent of [A]

Integrated rate law: [A]_t = [A]₀ − kt

Units of k: mol·L⁻¹·s⁻¹

Half-Life

At half-life, [R] = [R]₀ / 2

t_1/2 = [R]₀ / (2k)

t_1/2 is directly proportional to initial concentration

First Order Reactions

Rate Law

Rate = −d[R]/dt = k[R]

A graph Plot of ln[A] vs. time is linear with slope = −k

Rate depends linearly on [A]

Integrated rate law: ln[A]_t = ln[A]₀ − kt

Units of k: s⁻¹

Half-life is constant:

t_1/2 = 0.693 / k

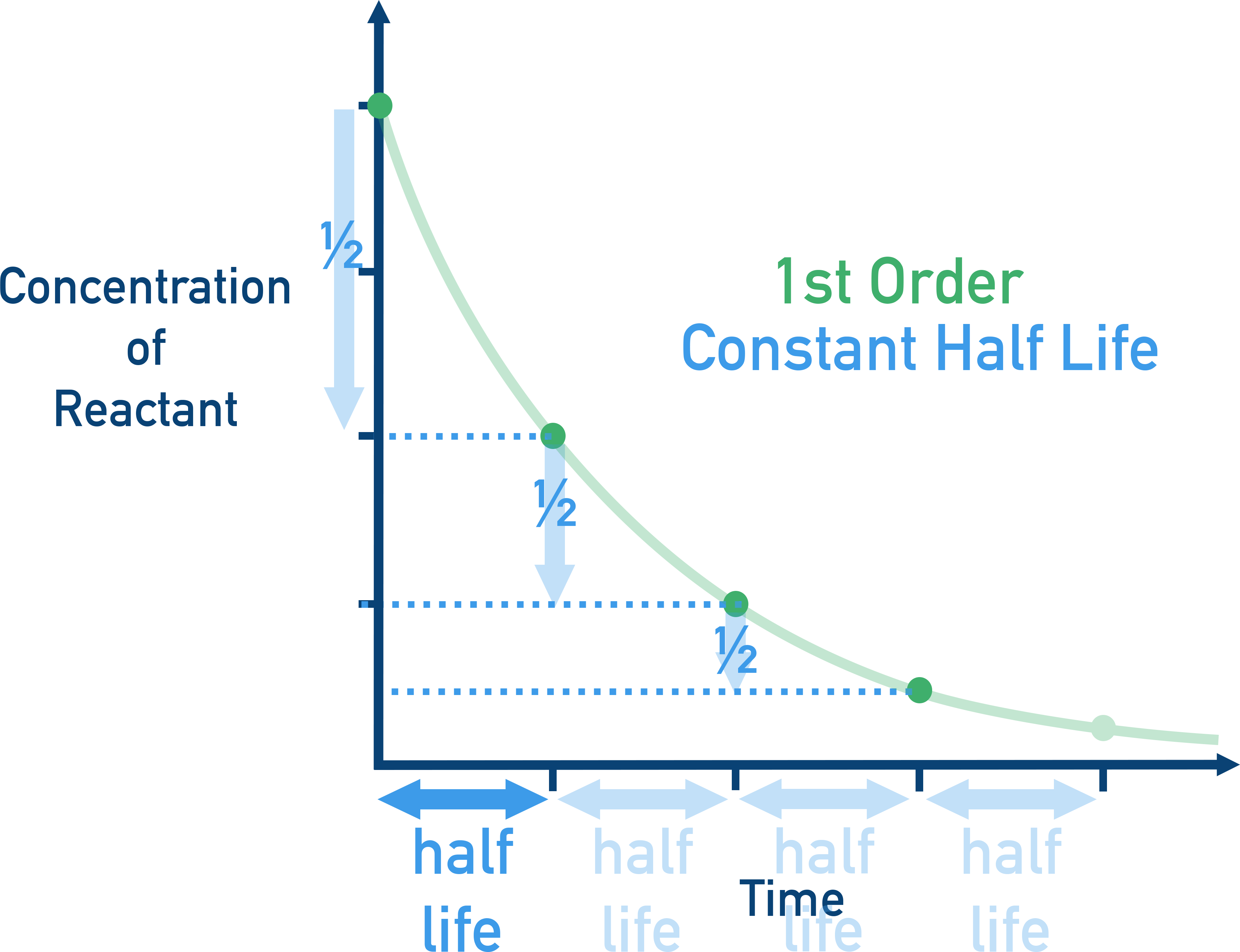
Half-Life of a Reaction

The half-life of a reaction, denoted as t_1/2, is the time required for the concentration of a reactant to decrease to half of its initial value.

For Zero Order Reaction:

Rate constant: k = ([R]₀ – [R]) / t

At t = t_1/2, [R] = ½ [R]₀

So, k = ([R]₀ – ½ [R]₀) / t_1/2 = ½ [R]₀ / t_1/2 ⇒ t_1/2 = [R]₀ / 2k

Conclusion: For zero-order reactions, half-life is directly proportional to initial concentration [R]₀.

For First Order Reaction:

Rate constant: k = (2.303 / t) × log([R]₀ / [R])

At t = t_1/2, [R] = ½ [R]₀

Substituting into the equation: k = (2.303 / t_1/2) × log(2) ⇒ t_1/2 = 0.693 / k

Conclusion: For first-order reactions, half-life is independent of [R]₀ and is constant.

Pseudo First Order Reactions

A pseudo first order reaction is a reaction that is not truly first order but behaves like one because one of the reactants is in large excess and its concentration effectively remains constant.

Example Hydrolysis of Ethyl Acetate

Reaction: CH₃COOC₂H₅ + H₂O → CH₃COOH + C₂H₅OH (in presence of acid H⁺)
Although this is a second-order reaction, water is in large excess. Its concentration remains nearly constant. So, the reaction behaves like a first order reaction with respect to ethyl acetate.

Example Inversion of Cane Sugar

Reaction: C₁₂H₂₂O₁₁ + H₂O → C₆H₁₂O₆ + C₆H₁₂O₆ (in presence of acid H⁺)
Rate = k [C₁₂H₂₂O₁₁]
Again, water is in excess, so it behaves like a first-order reaction.

Summary

• Integrated rate laws relate concentration to time for different reaction orders.
• Zero-order: [R] = [R]₀ − kt and t_1/2 = [R]₀ / (2k).
• First-order: ln[R] = ln[R]₀ − kt and t_1/2 = 0.693 / k.
• Pseudo first-order behavior arises when one reactant is in large excess.