Vapour Pressure of Liquid Solutions

NCERT Reference: Chapter 1 – Solutions – Page 9–11 (Part I)

Quick Notes

Vapour pressure: pressure exerted by vapour in equilibrium with its liquid.
For liquid–liquid solutions, total vapour pressure is the sum of partial vapour pressures.
Raoult’s Law: p₁ = x₁ × p₁^°, where p₁^° is vapour pressure of pure solvent.
Ideal solution: obeys Raoult’s law across composition.
Non-ideal solutions: show deviations due to intermolecular interactions.
Raoult’s law is a special case of Henry’s Law.
Vapour pressure of solid-in-liquid solutions depends only on the solvent’s contribution.

Full Notes

When a liquid is placed in a closed container, molecules escape into the vapour phase until a dynamic equilibrium is reached. The vapour pressure at this equilibrium reflects the tendency of molecules to escape.

When a non-volatile solute or another liquid is added, this equilibrium shifts and vapour pressure changes. This section explores how vapour pressure behaves in different types of liquid solutions.

Vapour Pressure of Liquid–Liquid Solutions

Consider a binary solution with two volatile liquids: component 1 and component 2.

In a closed container, both components evaporate until equilibrium is established between the vapour phase and the liquid phase.

NCERT Class 12 Chemistry diagram showing vapour–liquid equilibrium for a binary liquid solution with both components evaporating until dynamic equilibrium is reached.

Raoult’s Law

The partial vapour pressure of each component is directly proportional to its mole fraction in the solution.

For component A: p_A = x_A × p_A^°

For component B: p_B = x_B × p_B^°

Total Vapour Pressure (Dalton’s Law)

The total vapour pressure is based on partial pressures of both A and B (pA + pB), given by Dalton's Law.

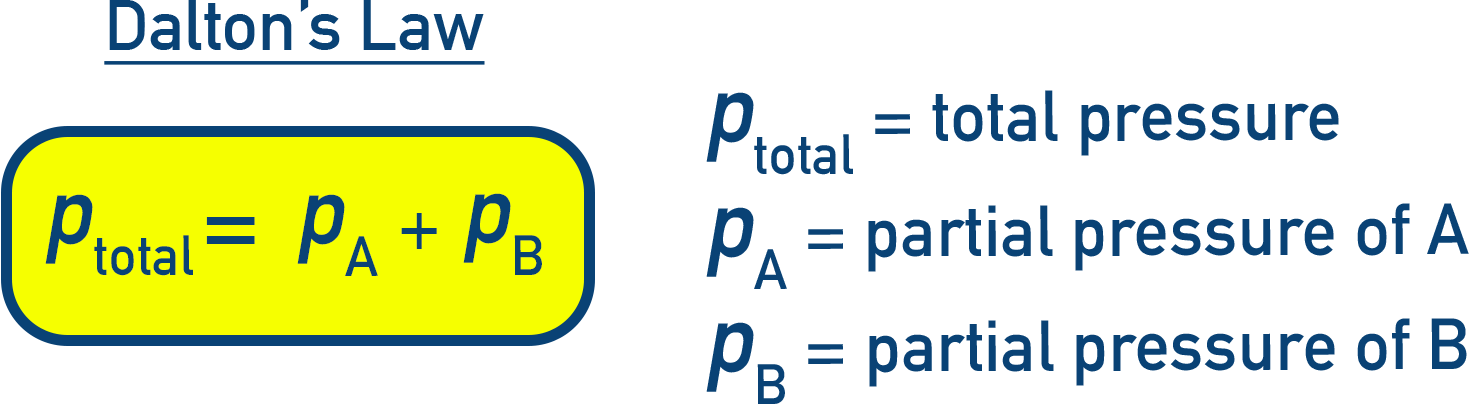
NCERT Class 12 Chemistry application of Dalton’s law showing total vapour pressure as the sum of partial pressures for a binary liquid solution.

p_total = p_A + p_B = x_A × p_A^° + x_B × p_B^°

Using x_A = 1 − x_B, we can write:

p_total = p_A^° + (p_B^° − p_A^°) × x_B

$NCERT Class 12 Chemistry linear plots of total vapour pressure versus mole fraction for an ideal binary liquid solution with endpoints at the pure-component vapour pressures.$

p_total depends on mole fraction of either component.
It varies linearly with x_B.
Minimum value: p_total = p_A^° when x_B = 0
Maximum value: p_total = p_B^° when x_B = 1

Vapour Phase Composition

Let y_A and y_B be the mole fractions of components A and B in vapour phase:

p_A = y_A × p_total p_B = y_B × p_total

So, y_A = p_A / p_total and y_B = p_B / p_total

Conclusion: Vapour phase always contains proportionally more of the more volatile component (the one with higher p^°).

Raoult’s Law as a Special Case of Henry’s Law

$NCERT Class 12 Chemistry comparison of Henry’s law p = KH × x and Raoult’s law p = x × p° as linear relations between partial pressure and mole fraction.$

Henry’s Law (for gases): p = K_H × x

Raoult’s Law (for liquids): p = x × p^°

Both show a linear relation between pressure and mole fraction. So, Raoult’s law is a special case of Henry’s law where the constant K_H = p^°.

Vapour Pressure of Solutions of Solids in Liquids

For non-volatile solutes, only solvent molecules contribute to vapour pressure.

The presence of solute particles reduces the surface area available for solvent to evaporate.

NCERT Class 12 Chemistry schematic showing reduction in solvent surface sites available for evaporation when a non-volatile solute is present.

As a result, vapour pressure of the solution is less than that of the pure solvent. The decrease depends on the amount of solute present, not its nature.

Raoult’s Law (for Non-Volatile Solute)

Raoult's Law can be adjusted for solutions where the solute is non-volatile (won't leave the solution as a vapour).

$NCERT Class 12 Chemistry Raoult’s law for non-volatile solute p1 = x1 × p1° with a linear plot of solvent vapour pressure versus its mole fraction.$

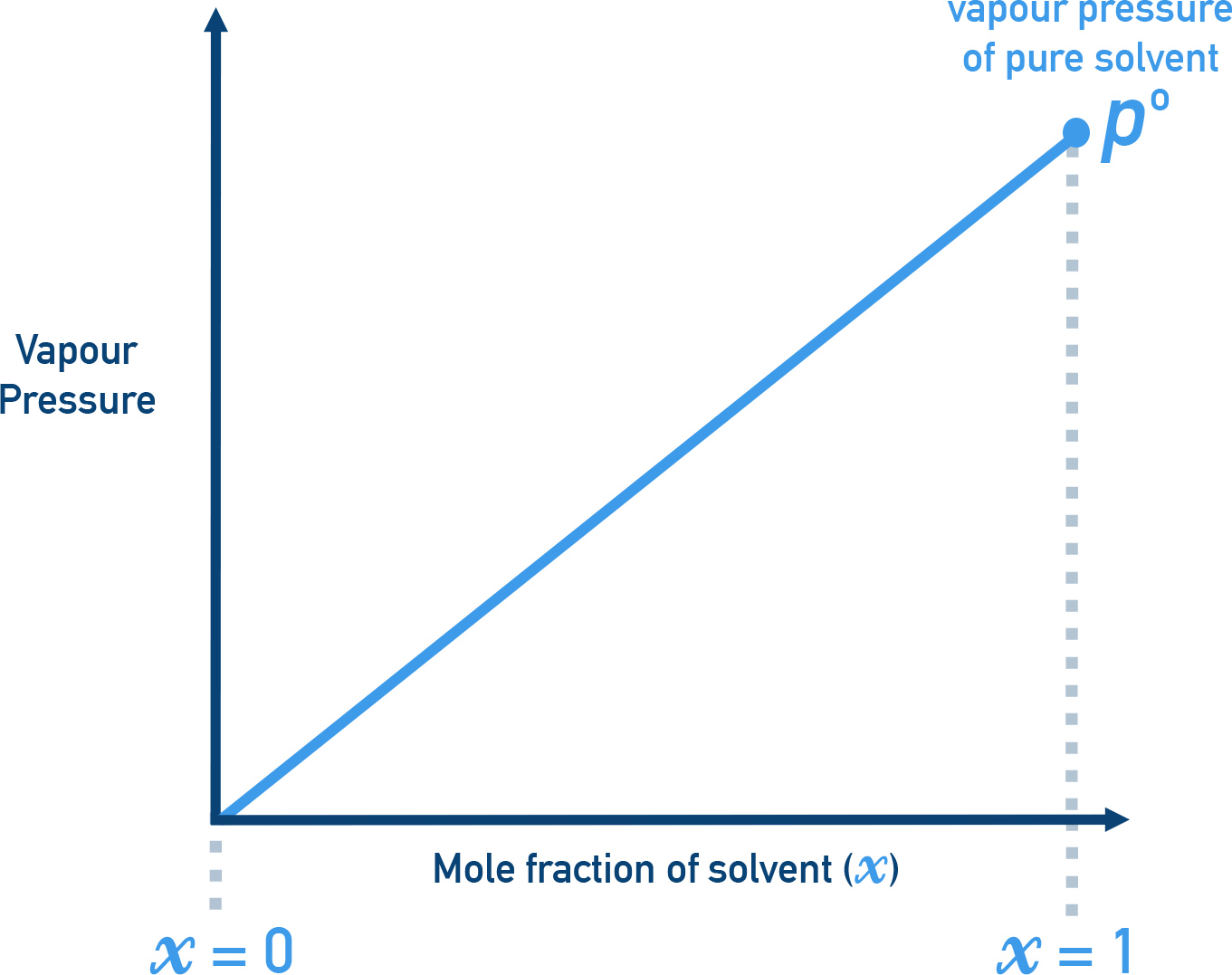
Let x₁ = mole fraction of solvent and p₁^° = vapour pressure of pure solvent. Then:

p₁ = x₁ × p₁^°

This gives a linear graph of vapour pressure vs mole fraction of solvent.

$NCERT Class 12 Chemistry linear relation of solvent vapour pressure with solvent mole fraction for a solution containing a non-volatile solute.$

Summary

Raoult’s law states partial vapour pressure is proportional to mole fraction for each volatile component.
Total vapour pressure equals the sum of partial pressures in liquid–liquid solutions.
Ideal solutions obey Raoult’s law across composition while non-ideal solutions deviate.
Raoult’s law is a special case of Henry’s law with K_H equal to the pure component vapour pressure.
For solid–liquid solutions with non-volatile solute only the solvent contributes to vapour pressure.