pH Calculations, Ka and Kw

Full Notes

What is pH?

The pH scale measures the concentration of hydrogen ions (H⁺) in solution, on a logarithmic scale. This allows us to express a wide range of H⁺ concentrations more simply.

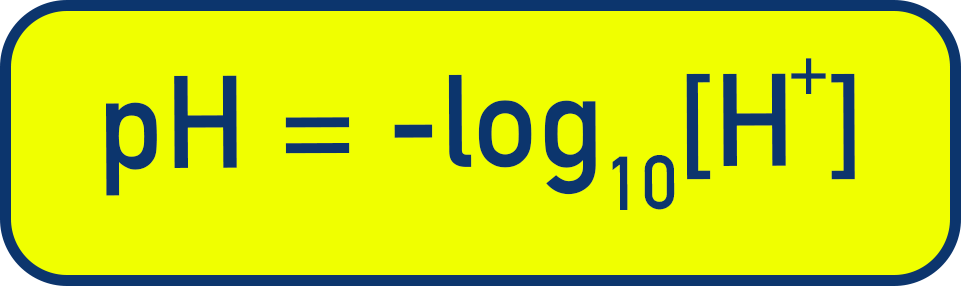
A lower pH indicates a higher concentration of hydrogen ions (i.e. a more acidic solution).

To work backwards and calculate [H⁺] from pH:

This is useful when you’re given a pH value and need to calculate the hydrogen ion concentration, such as in weak acid problems.

Strong Acids and pH

Strong acids fully dissociate in solution.

This means the concentration of hydrogen ions equals the concentration of the acid (for monoprotic acids such as HCl).

For Example Strong acid pH

For 0.01 mol dm⁻³ HCl:
[H⁺] = 0.01 mol dm⁻³
pH = –log(0.01) = 2.00

Because there's no equilibrium to consider, these pH calculations are straightforward.

Weak Acids and K_a

Weak acids only partially dissociate in solution, setting up an equilibrium:

The acid dissociation constant (K_a) is the equilibrium constant used for weak acid dissociation:

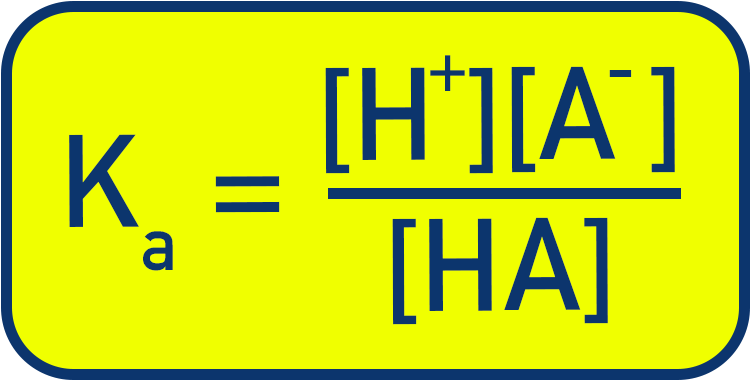
Where:

• [H⁺] and [A⁻] are concentrations of the dissociated ions
• [HA] is the concentration of the undissociated acid

The larger the K_a, the more the acid dissociates = stronger acid.
The smaller the K_a, the less it dissociates = weaker acid.

Introducing pK_a

K_a values for weak acids are often very small, so it is sometimes easier to use pK_a:

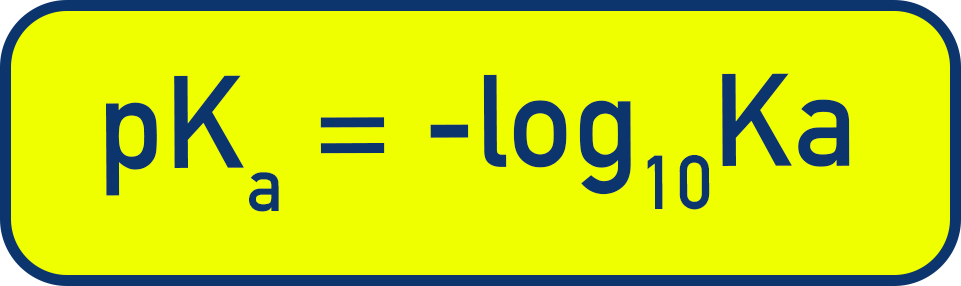
This is simply a more manageable number and a lower pK_a = stronger acid.

You can also calculate K_a from pK_a using:

Calculating pH of a Weak Acid

You can calculate the pH of a weak acid using its K_a value and its concentration.

Since weak acids partially dissociate with H⁺ and A⁻ in a 1:1 ratio, we assume:

• [H⁺] is approximately equal (≈) to [A⁻] (from HA dissociation)
• [HA] remains nearly unchanged

This means we can assume that [H⁺] × [A⁻] = [H⁺]².

K_a = ([H⁺]²) / [HA] and as a result [H⁺] = √(K_a × [HA]).

Steps to Calculate pH of a Weak Acid

1. Use K_a expression:
   K_a = ([H⁺]²) / [HA]
2. Rearrange to find [H⁺]:
   [H⁺] = √(K_a × [HA])
3. Find pH:
   pH = –log[H⁺]

Matt’s exam tip

Don’t forget when using K_a to find the pH of a weak acid, we are assuming two things — one that [H⁺] = [A⁻] and that the [HA] at the start is the same as the concentration of weak acid at equilibrium. These are assumptions: for example the [HA] at equilibrium won’t be exactly the same as the initial [HA] as some will have dissociated, however the amount of dissociation is very small compared to the concentration meaning mathematically it isn’t significant enough for us to worry about.

Using Experimental pH to Find K_a

You may be given the pH of a weak acid solution and asked to find K_a. Follow these steps:

1. Convert pH to [H⁺]: [H⁺] = 10^(–pH)
2. Assume [H⁺] = [A⁻]
3. Use original acid concentration as [HA] (approximate)
4. Plug into: K_a = [H⁺]² / [HA]

This is a common exam question.

The Ionic Product of Water (K_w)

In water, a very small percentage of molecules ionise, releasing H⁺ and OH⁻ ions into solution.

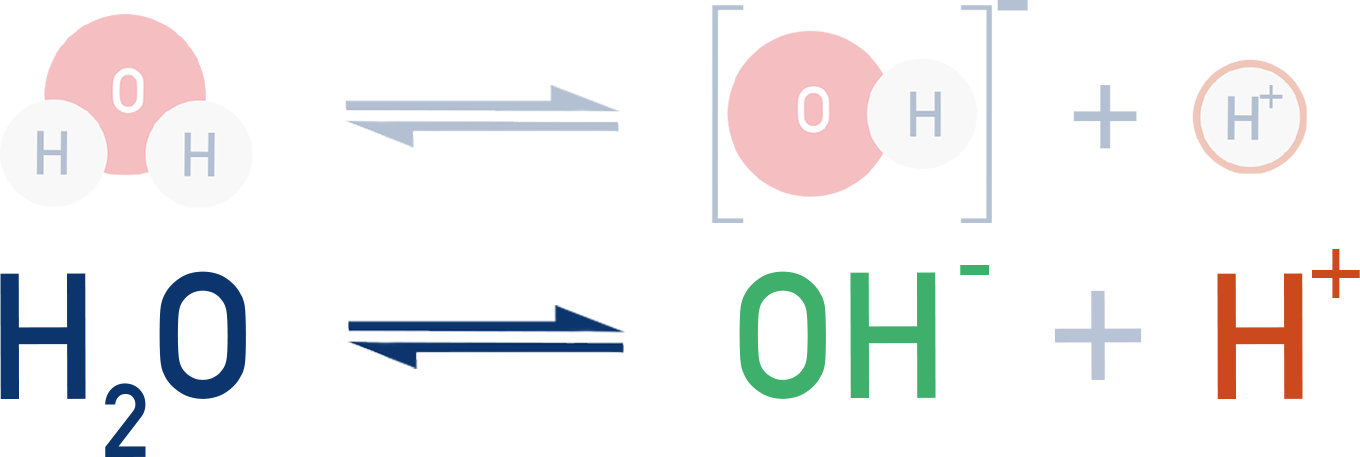
This is a reversible process and an equilibrium is established.

The equilibrium constant for this is:

For a more detailed explanation on K_w and where it comes from, see here.

At 298 K: K_w = 1.0 × 10⁻¹⁴ mol² dm⁻⁶
K_w is key for finding pH of bases, because strong bases increase [OH⁻].

Calculating pH of Strong Bases

To calculate the pH of a strong base like NaOH:

1. [OH⁻] = concentration of the base
2. Use K_w to find [H⁺]
3. Use [H⁺] to find pH

Using pK_w

Just like K_a and pK_a, we can define:

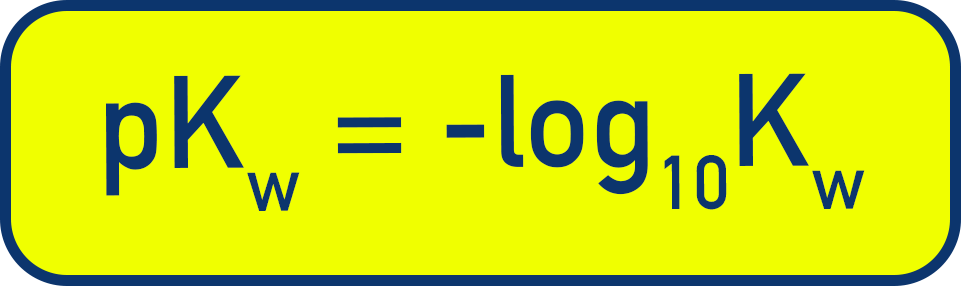
At 298 K, pK_w = 14.

Summary

• pH measures hydrogen ion concentration using a logarithmic scale.
• Strong acids fully dissociate and weak acids partially dissociate with K_a the equilibrium constant.
• pK_a is a convenient way to compare acid strengths (lower pK_a = stronger acid).
• K_w links [H⁺] and [OH⁻] in water and at 298 K, K_w = 1.0 × 10⁻¹⁴.
• For weak acids, use K_a and concentration to calculate [H⁺] and pH.
• For strong bases, calculate [OH⁻], then find [H⁺] from K_w.
• pK_w = 14 at 298 K.