Equations and Calculations Involving Moles
Quick Notes
- Chemical equations must always be balanced in terms of molar ratios. They can include state symbols: (s), (l), (g), (aq) where appropriate.
- Ionic equations show only species involved in a reaction that actually change. They don't include spectator ions.
- Use n = c × V (volume in dm³) for solution calculations.
- Use pV = nRT (ideal gas law) for gases under non-standard conditions.
- Titration data allows you to calculate moles, volume, or concentration.
- Indicators can be used in acid-base titrations to allow end points to be observed:
- Phenolphthalein (pink to colourless)
- Methyl orange (yellow to red)
Full Notes
Writing Full and Ionic Equations
Full chemical equations show all reactants and products, including physical states.
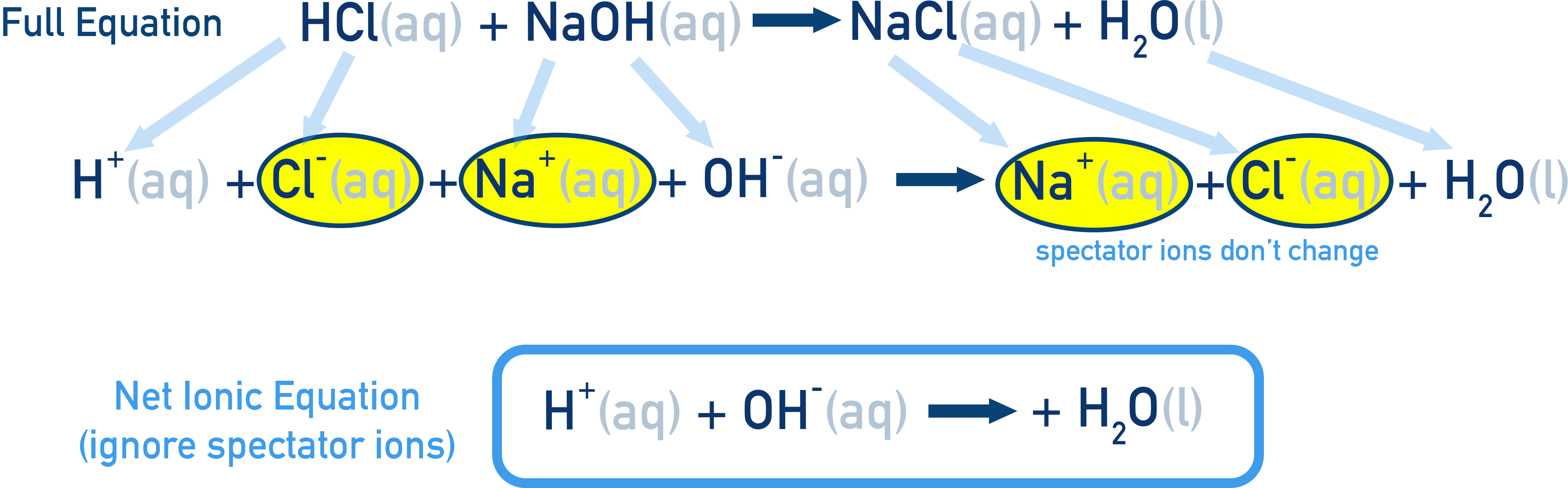
Example Reaction between NaOH and HCl
Full equation: NaOH(aq) + HCl(aq) → NaCl(aq) + H2O(l)
Ionic equation: OH−(aq) + H+(aq) → H2O(l)
Calculating Moles
We can use different equations to calculate moles, depending on the type of substances and the data given.
- From mass: moles = mass ÷ Mr
- From gas volume at RTP: moles = volume (dm³) ÷ 24.0
- From solution: moles = concentration × volume (dm³)
To convert cm³ to dm³: divide by 1000
Calculating Reacting Masses
When calculating masses of reactants and products, always use the balanced chemical equation and follow these steps:
- Calculate moles of the known substance.
- Use mole ratio to find moles of unknown.
- Multiply by Mr to get mass.
Calculate the mass of CO2 formed from 10.0 g of CaCO3.
- Equation: CaCO3 → CaO + CO2
- Moles of CaCO3 = 10.0 ÷ 100.1 = 0.100 mol
- Moles of CO2 = 0.100 mol
- Mass of CO2 = 0.100 × 44.0 = 4.4 g

Always write out workings in full and clearly labelled. This helps you keep track of your answer and enables easy checking at the end of an exam.
Calculating Volumes of Gases
At RTP (Room Temperature and Pressure): volume = moles × 24.0 (dm³)
Calculate the volume of H2 formed when 0.05 moles of Mg reacts.
- Equation: Mg + 2HCl → MgCl2 + H2
- 0.05 mol Mg gives 0.05 mol H2
- Volume = 0.05 × 24.0 = 1.20 dm³

Remember the molar volume of a gas is only for a specific temperature and pressure. If a question doesn’t specify room temperature and pressure (RTP), you can’t assume 24 dm³ mol⁻¹.
The Ideal Gas Equation
See ideal gas equation for more detail.
pV = nRT
- P in Pa
- V in m³
- T in K
- R = 8.314 J mol⁻¹ K⁻¹
- Convert units before substituting.

Always convert units at the start of an ideal gas equation question. Remember to get volume from cm³ to m³, divide by 1 × 10⁶.
Calculate the volume occupied by 0.20 mol gas at 298 K and 100 kPa.
- P = 100,000 Pa
- V = (0.20 × 8.314 × 298) ÷ 100,000
- = 0.00495 m³ = 4.95 dm³
Titration Calculations
Titrations form the basis of required practical 3, outlined here in detail. Titrations are also covered more fully later in the course here.
Neutralisation reactions between acids and alkalis allow us to calculate the concentration of a solution of acid or base by reacting it with a known volume and concentration of a base or acid.
moles = concentration × volume (dm³)
Indicators are used that change colour to indicate when sufficient volume of acid or base has been added to react completely with the original solution:
- Phenolphthalein: pink in alkali, colourless in acid
- Methyl orange: yellow in alkali, red in acid
25.0 cm³ NaOH neutralises 27.3 cm³ of 0.100 mol dm⁻³ HCl. Find the concentration of NaOH solution.
- Moles HCl = 0.100 × (27.3 ÷ 1000) = 0.00273 mol
- Moles NaOH = 0.00273 mol (1:1 ratio)
- C(NaOH) = 0.00273 ÷ (25.0 ÷ 1000) = 0.109 mol dm⁻³
Summary
- Chemical equations must be balanced using molar ratios.
- Ionic equations show only the species that change.
- Moles can be calculated from mass, gas volume or solution data.
- Reacting mass calculations use balanced equations and mole ratios.
- Gas volumes at RTP use 24.0 dm³ mol⁻¹, or use pV = nRT for other conditions.
- Titrations allow calculation of unknown concentrations using neutralisation.
- Indicators show end points in acid-base titrations.
