The Mole, Formulae and Basic Calculations

Specification Reference Topic 5 points 1–5 (Edexcel Chemistry)

Quick Notes

The mole (mol) is the unit used to measure amount of substance in chemistry.
Avogadro constant (L or N_A) = 6.02 × 10²³ mol⁻¹ is the number of particles in one mole.
Molar mass (g mol⁻¹) = mass of one mole of a substance (same value as Mr).
Empirical formula shows the simplest whole-number ratio of atoms in a compound.
Molecular formula shows the actual number of atoms in a molecule.
Use mass, Mr and moles in mole calculations.
- Moles = mass ÷ Mr
- Ideal gas equation pV = nRT.

Full Notes

The Mole and Avogadro Constant

The mole is a fundamental unit in chemistry, representing the amount of substance that contains the same number of particles as there are atoms in exactly 12 g of carbon-12. This number is the Avogadro constant:

Avogadro constant (L or N_A) = 6.02 × 10²³ mol⁻¹

This number applies to any type of particle: atoms, molecules, ions, or electrons.

Example One mole of particles

1 mole of oxygen molecules (O₂) contains 6.02 × 10²³ O₂ molecules.
1 mole of sodium chloride contains 6.02 × 10²³ Na⁺ and 6.02 × 10²³ Cl⁻ ions.

Molar Mass and Calculating Moles

The molar mass (in g mol⁻¹) of a substance is the mass of one mole of its particles.

To calculate the number of moles from mass:

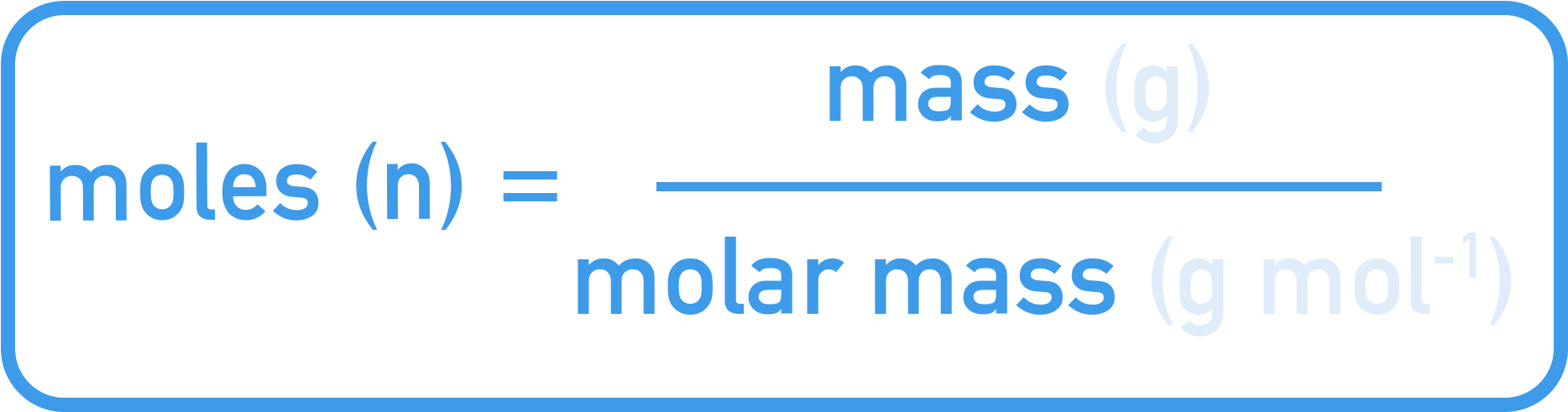
Edexcel A-Level Chemistry diagram showing method to calculate number of moles from mass.

Worked Example

How many moles in 18 g of water (H₂O)?

Mr of H₂O = 2(1) + 16.0 = 18.0
Moles = mass ÷ Mr = 18 ÷ 18.0 = 1 mol

Worked Example 2

What is the mass of 2 moles of methane (CH₄)?

Mr of CH₄ = 4(1.0) + 12.0 = 16.0
If Moles = mass ÷ Mr, then Mass = Moles × Mr
Mass = 2 × 16.0 = 32 g

To calculate the number of particles of something:

Worked Example

How many molecules in 0.5 mol of O₂?

Number of molecules = 0.5 × N_A
= 0.5 × (6.02 × 10²³) = 3.01 × 10²³

Matt’s exam tip

When working with the Avogadro constant, don’t be surprised if answers seem very big (when finding numbers of particles) or very small (finding masses of individual particles). Remember the Avogadro constant is enormous!

Empirical and Molecular Formulae

The empirical formula shows the simplest whole number ratio of atoms in a compound and the molecular formula represents the actual number of atoms in a molecule.

Example Glucose (C₆H₁₂O₆)

Empirical formula = CH₂O (simplest ratio 1:2:1)
Molecular formula = C₆H₁₂O₆ (actual composition)

To find the empirical formula from composition:

Convert mass or % to moles (divide by Ar).
Divide all mole values by the smallest.
Write the simplest ratio.

To find molecular formula:

Calculate Mr of the empirical formula.
Divide molecular Mr by empirical Mr.
Multiply the empirical formula by this number.

Worked Example

Find the empirical formula for the compound with a composition by mass of C 52.2%, H 13.0% and O 34.8%.

The Ideal Gas Equation

The background theory behind ideal gases and the ideal gas equation has been covered in more detail here.

The ideal gas equation is pV = nRT

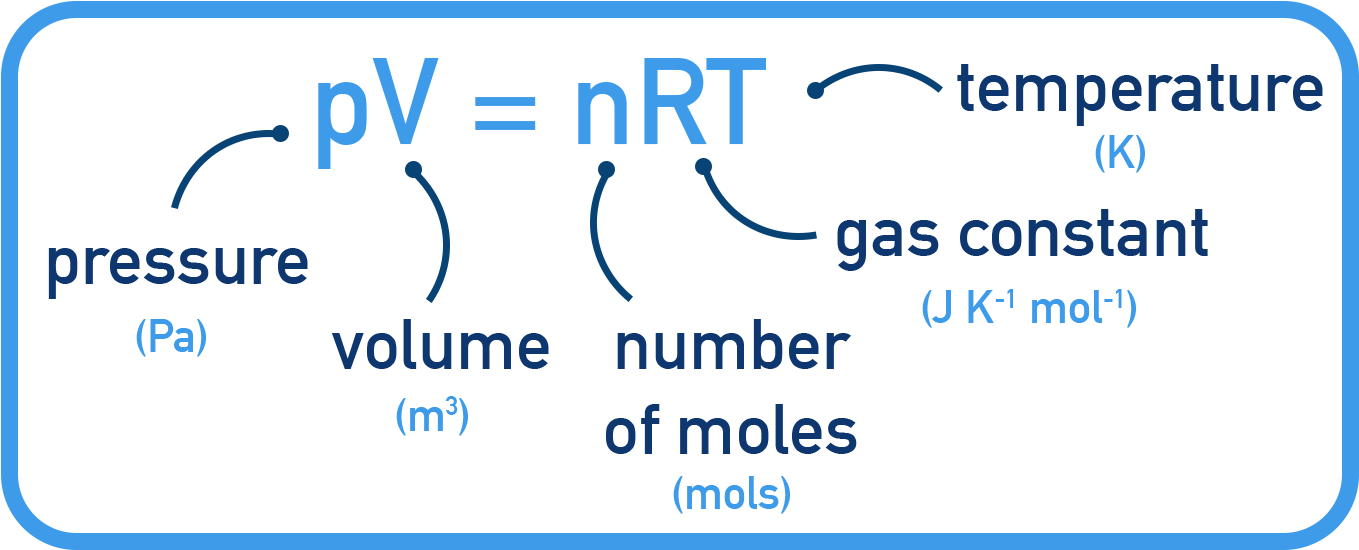
Edexcel A-Level Chemistry diagram showing ideal gas equation pV = nRT with parameters pressure, volume, temperature and moles.

This equation relates pressure (P), volume (V), temperature (T), and moles (n) of a gas. The gas constant (R) has a value of 8.314 J mol⁻¹ K⁻¹.

Symbol	Meaning	SI Unit
P	Pressure	Pascals (Pa)
V	Volume	Cubic meters (m³)
n	Moles of gas	moles (mol)
R	Gas constant	8.314 J mol⁻¹ K⁻¹
T	Temperature	Kelvin (K)

Unit Conversions for the Ideal Gas Equation

All values must be in SI units before using the equation:

Pressure Conversions
- 1 atm = 101,325 Pa
- 1 kPa = 1,000 Pa
Volume Conversions
- 1 dm³ = 0.001 m³
- 1 cm³ = 0.000001 m³
Temperature Conversion
- Always use Kelvin (K)
- Convert from Celsius: T(K) = T(°C) + 273.15

Ideal vs. Real Gases

The ideal gas law assumes:

Gas particles have no volume.
No intermolecular forces exist.
Collisions are elastic (no energy loss).

However, real gases deviate from ideal behavior:

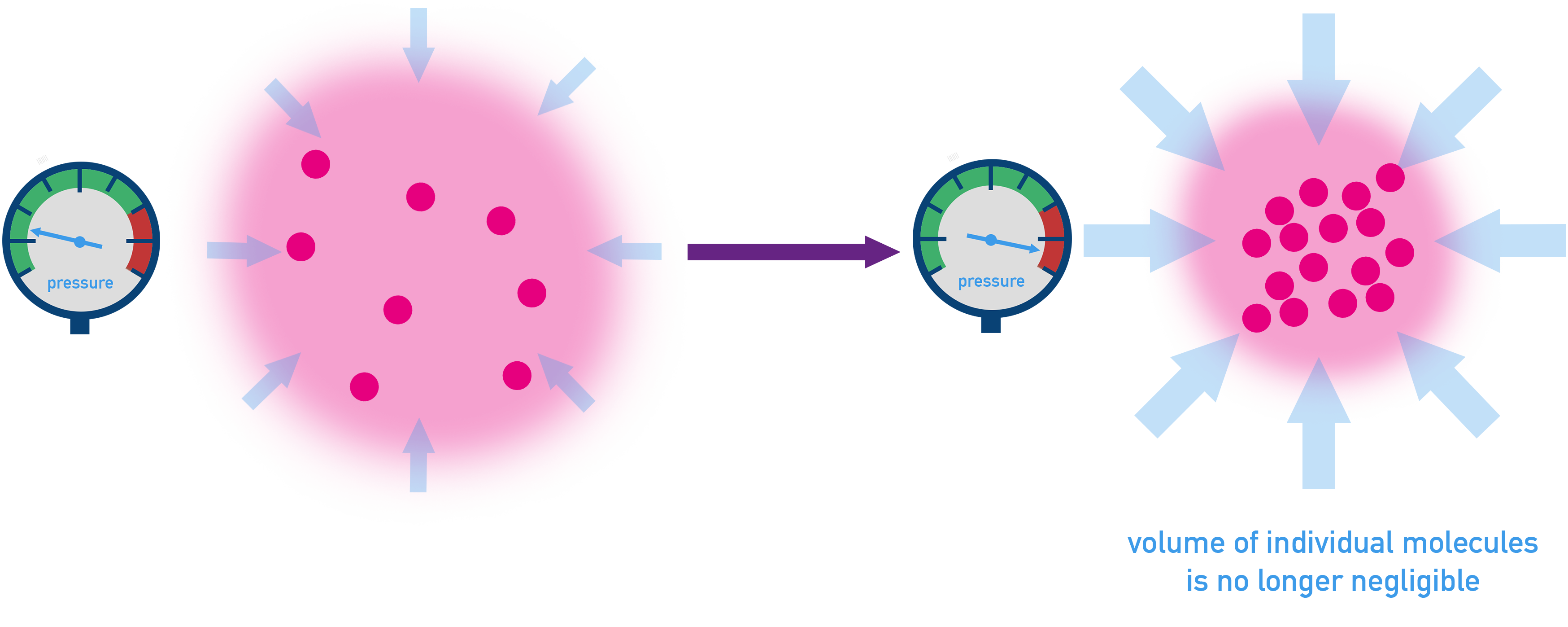
At high pressures, gas particles occupy space, meaning their volume is no longer negligible.

Edexcel A-Level Chemistry graph showing deviation from ideal gas behaviour at high pressures due to finite particle volume.

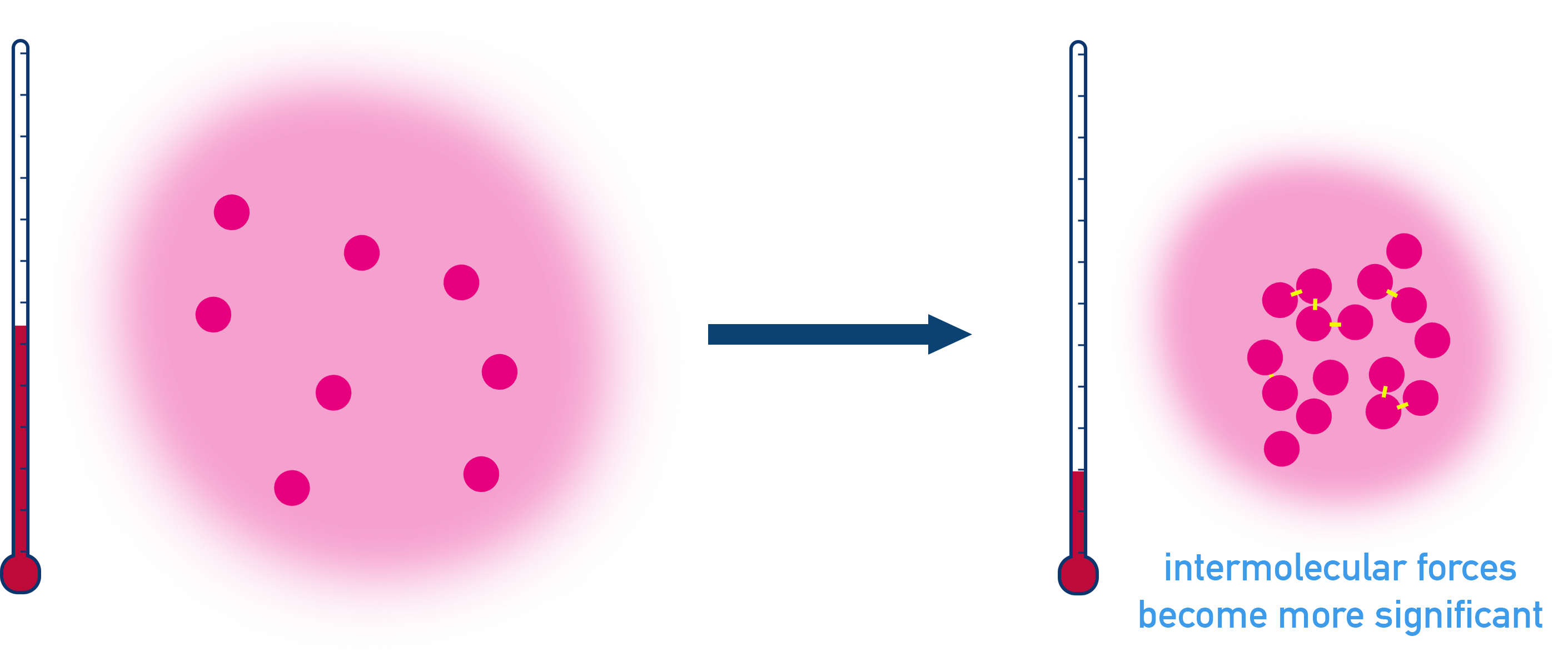
At low temperatures, intermolecular forces become significant, making gases more likely to condense.

Edexcel A-Level Chemistry graph showing deviation from ideal gas behaviour at low temperature due to intermolecular forces.

Summary

The mole measures amount of substance, defined using the Avogadro constant.
Moles = mass ÷ Mr and are used in mole calculations.
Molar mass is the mass of one mole of a substance.
Empirical formula is the simplest ratio, molecular formula gives actual composition.
The ideal gas equation pV = nRT relates pressure, volume, moles and temperature.
Values must be in SI units when applying the ideal gas equation.
Real gases deviate from ideal behaviour at high pressure and low temperature.