Lattice Energy

Full Notes

Lattice enthalpies and Born–Haber cycles have been outlined in more detail here.
This page is just what you need to know for Edexcel A-level :)

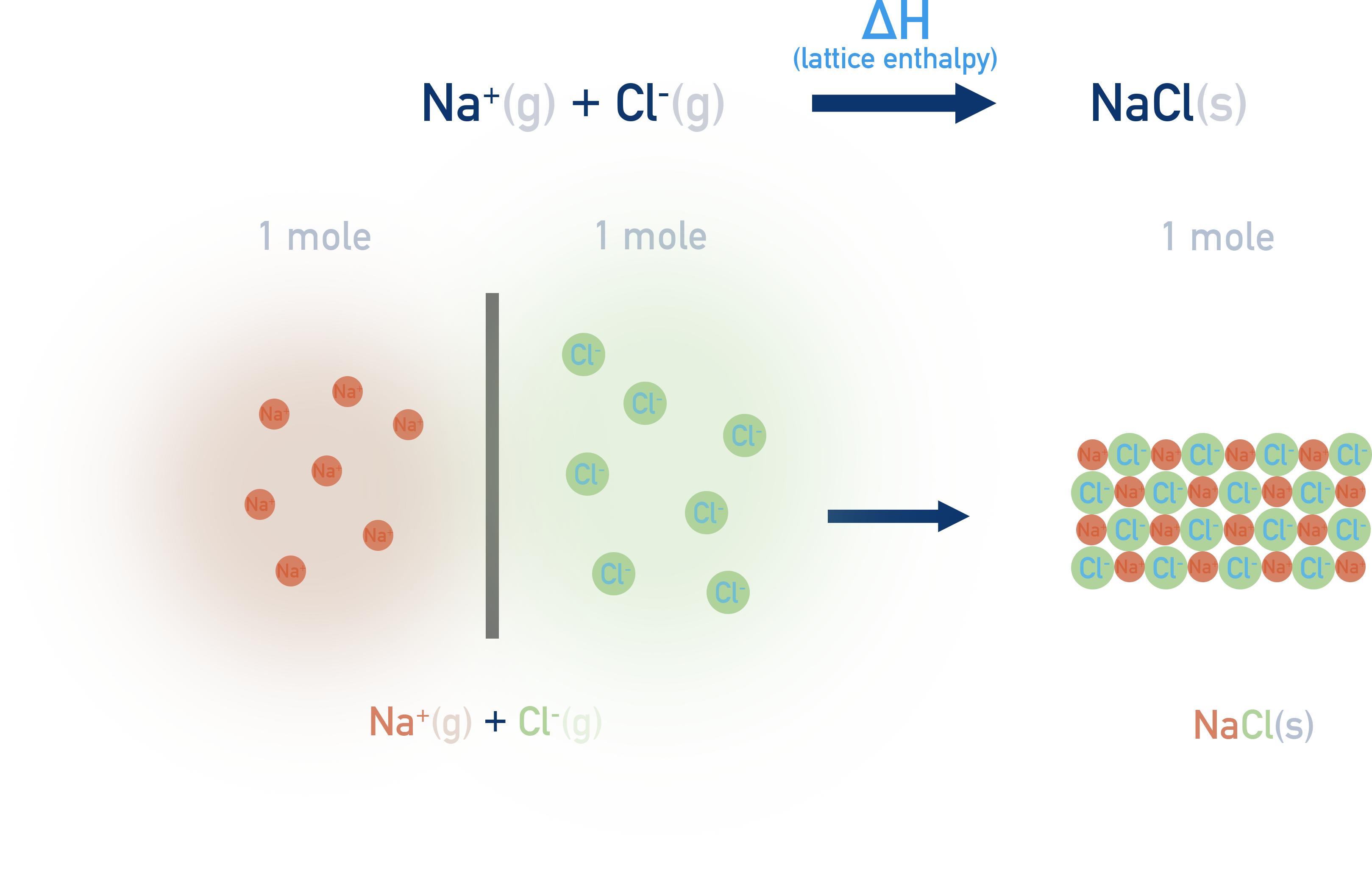
Lattice energy (ΔH_latt) refers to the energy change associated with the formation of an ionic solid from its gaseous ions. It can be considered a measurement of the bonding strength in ionic compounds.

Lattice energies can’t be measured directly in an experiment however can be determined using experimental data with Hess’s Law.

Born–Haber cycles are a type of Hess cycle used to calculate lattice energy.

Key Definitions

Enthalpy change of atomisation (ΔH_at):
The enthalpy change when 1 mole of gaseous atoms is formed from an element in its standard state.
Example Na(s) → Na(g)

Lattice energy (ΔH_latt):
The enthalpy change when 1 mole of an ionic solid is formed from its gaseous ions.
Example Na⁺(g) + Cl⁻(g) → NaCl(s)
Lattice energy is always exothermic (negative value).

Electron Affinity

• First electron affinity is the energy change when 1 mole of gaseous atoms gains electrons to form 1 mole of 1⁻ ions.
  Example Cl(g) + e⁻ → Cl⁻(g)
  This is usually exothermic.
• Second electron affinity is for adding an electron to a negatively charged ion (e.g. O⁻ to O²⁻), and is endothermic due to repulsion.

Constructing a Born–Haber Cycle

1. Write the enthalpy of formation equation (solid compound from elements).
2. Convert elements to gaseous atoms (atomisation enthalpy).
3. Remove electrons from metal atoms (ionisation energy).
4. Add electrons to non-metal atoms (electron affinity).
5. Combine gaseous ions to form lattice (lattice enthalpy).

Example Born–Haber Cycle for NaCl

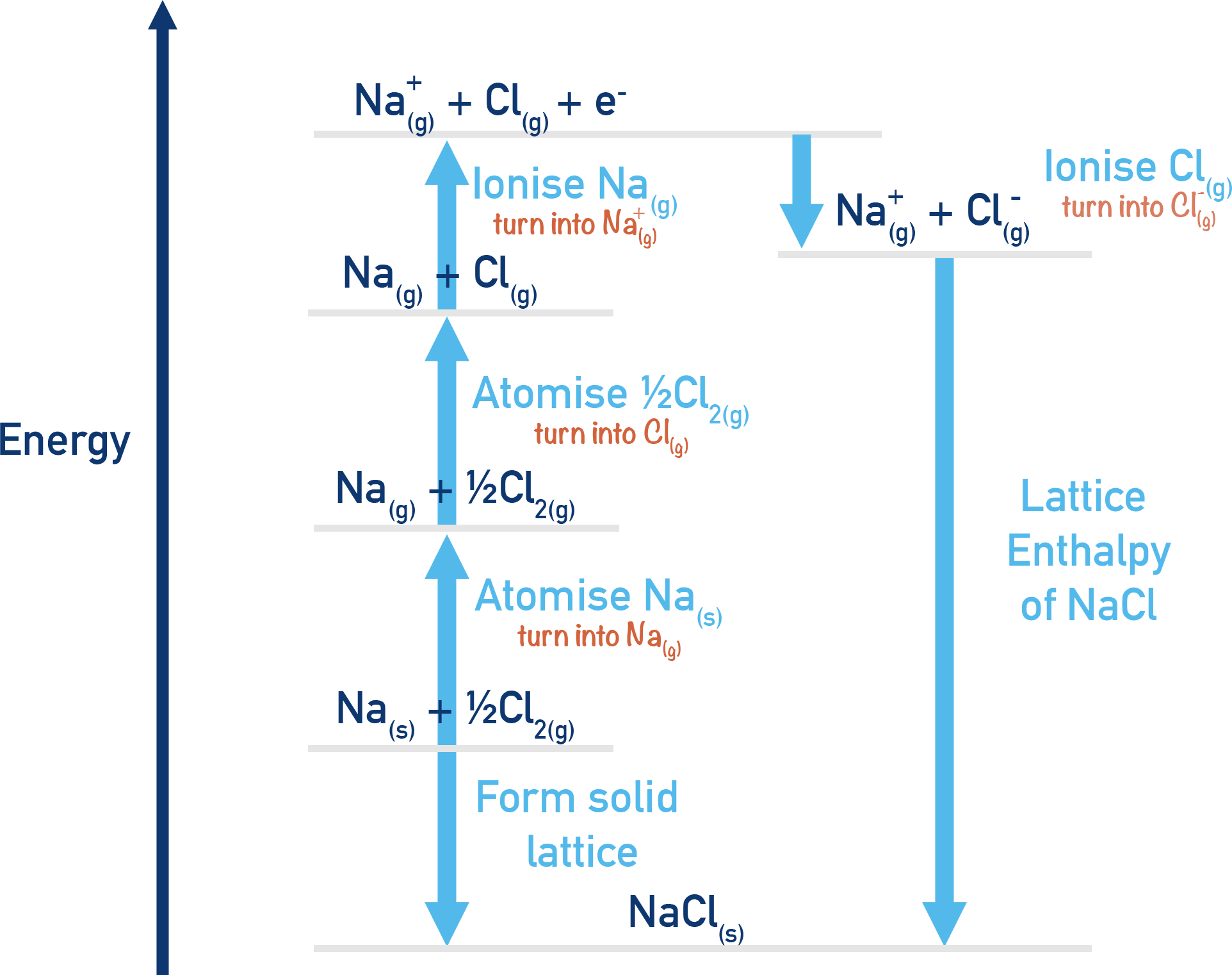
• Step 1: Formation of NaCl (ΔH_f)
  Na(s) + ½Cl₂(g) → NaCl(s)
• Step 2: Atomisation of Na (ΔH_atom)
  Na(s) → Na(g)
• Step 3: Atomisation of Cl₂ (ΔH_atom)
  ½Cl₂(g) → Cl(g)
• Step 4: Ionisation Energy of Na (IE₁)
  Na(g) → Na⁺(g) + e⁻
• Step 5: Electron Affinity of Cl (EA₁)
  Cl(g) + e⁻ → Cl⁻(g)
• Step 6: Lattice Enthalpy (ΔH_le)
  Na⁺(g) + Cl⁻(g) → NaCl(s)

By rearranging these enthalpy changes and substituting experimental values into the cycle we can use Hess’s Law to calculate ΔH_le.

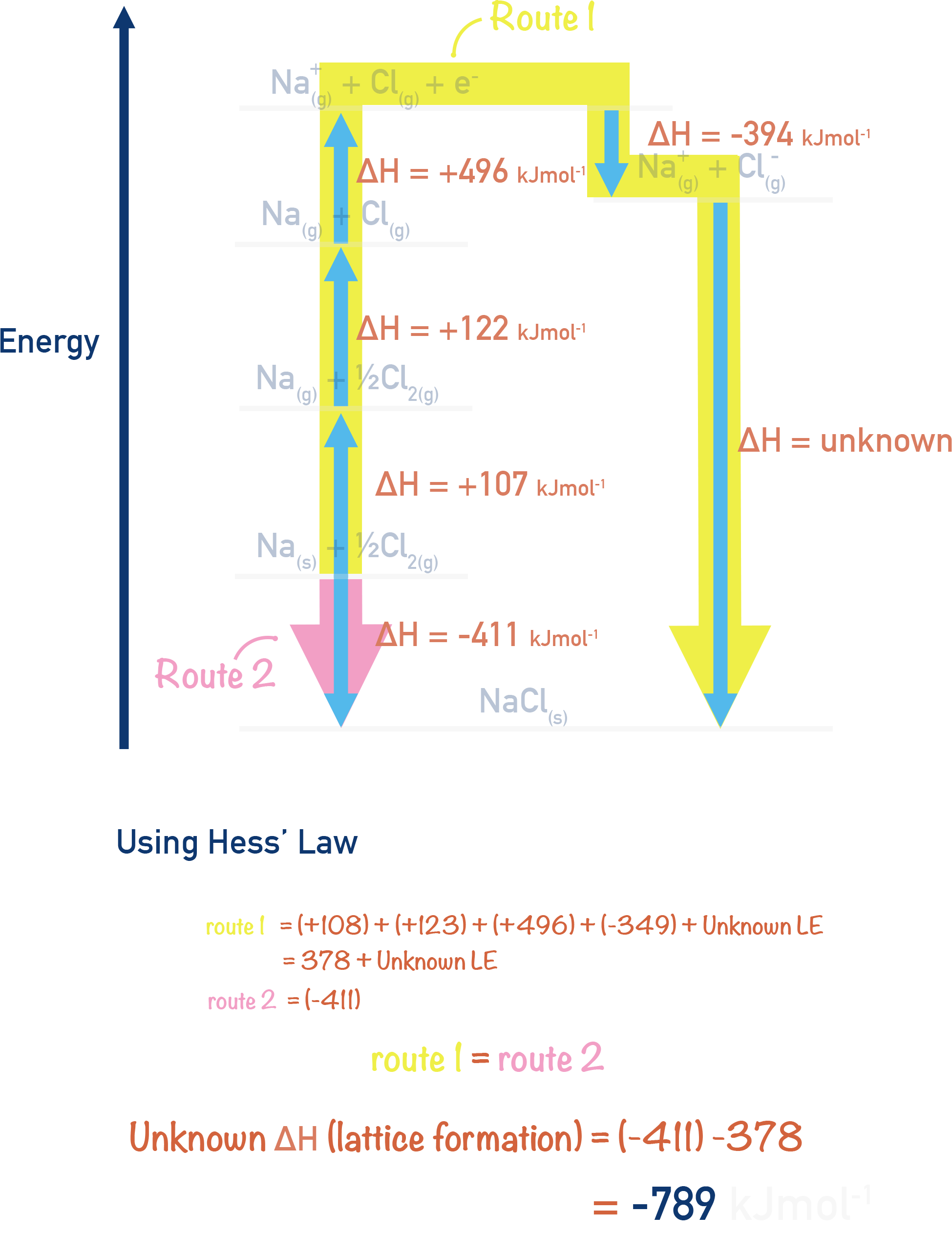
Bond Strength from Lattice Energy

A more negative (larger magnitude) lattice energy means stronger electrostatic attraction between ions. This allows us to use lattice energies as a measure of bonding strength in ionic compounds.

Factors Affecting Lattice Energy

Charge and ionic radius affect the magnitude of lattice energy:

• Charge: Higher ion charge = stronger electrostatic attraction between ions = more exothermic lattice energy.
  Example Mg²⁺ gives more exothermic lattice energies than Na⁺.
• Ionic radius: Smaller radius = stronger attraction = more exothermic lattice energy.

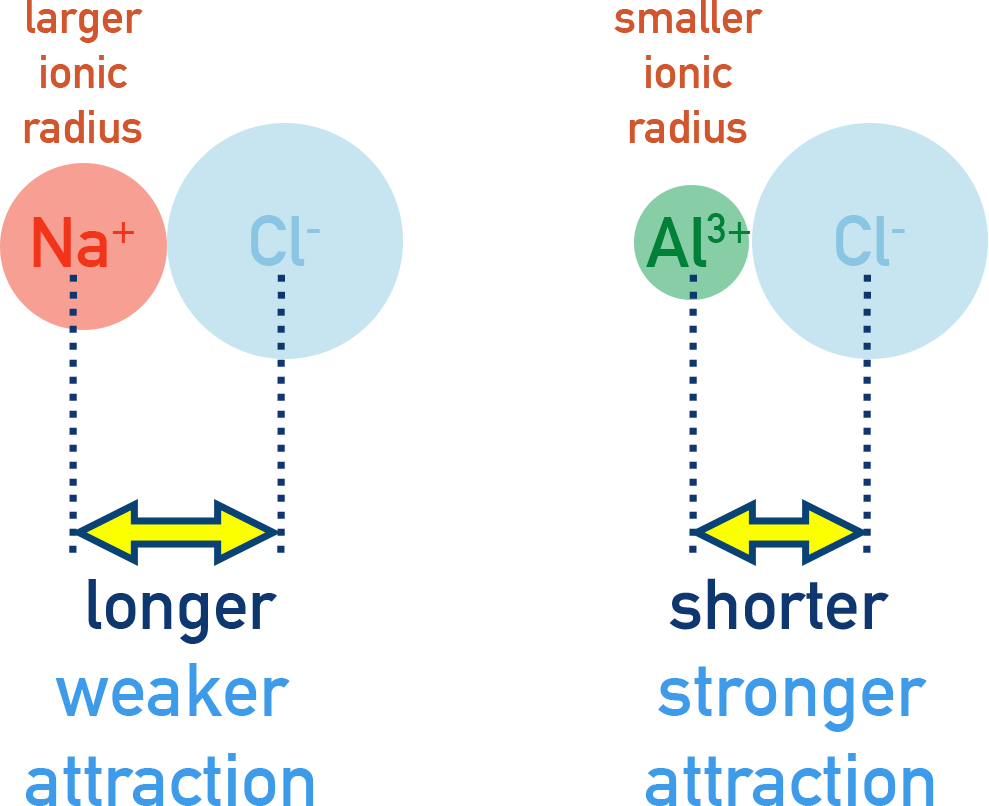
Down a group, ionic radius increases and lattice energy becomes less exothermic.

Comparing Experimental vs. Theoretical ΔLE

Born–Haber cycle values come from experimental data, meaning lattice enthalpies from Born-Haber cycle calculations are called experimental lattice enthalpies.

Theoretical lattice enthalpy assumes purely ionic bonding based on perfectly spherical ions with a uniform charge. They are calculated using theoretical data about the ions (size and charge) in the compound.

If experimental values differ from theoretical values, the compound has some covalent character due to polarisation of the anion by the cation.

The greater the difference between experimental and theoretical values, the greater the degree of covalent character in the compound.

Polarisation and Ionic Radii

Cations with high charge and small radius have strong polarising power.
Anions with low charge density (large radius, high charge) are easily polarised.
This causes distortion of the electron cloud and introduces covalent character into the bond.

Example Covalent character in ionic lattices

• NaCl is nearly purely ionic (experimental ≈ theoretical).
• AgCl has a higher experimental lattice enthalpy than theoretical, indicating covalent character.

This can be explained by the fact Ag⁺ ions are able to polarise Cl⁻ ions more than Na⁺ ions. The Cl⁻ ion doesn’t remain a perfect sphere and there is a small amount of electron sharing between the two ions, meaning the bonding in the crystal isn’t purely ionic — hence the theoretical value which assumes only ionic bonding doesn’t match the actual, experimental value.

Solution and Hydration Enthalpies

Born–Haber cycles can also be used when dealing with enthalpies of solution and hydration.

Enthalpy of solution (ΔH_sol):
The enthalpy change when 1 mole of an ionic compound dissolves in enough water to form an infinitely dilute solution.

Example NaCl(s) → Na⁺(aq) + Cl⁻(aq)

Enthalpy of hydration (ΔH_hyd):
The enthalpy change when 1 mole of gaseous ions dissolves in water to form aqueous ions.

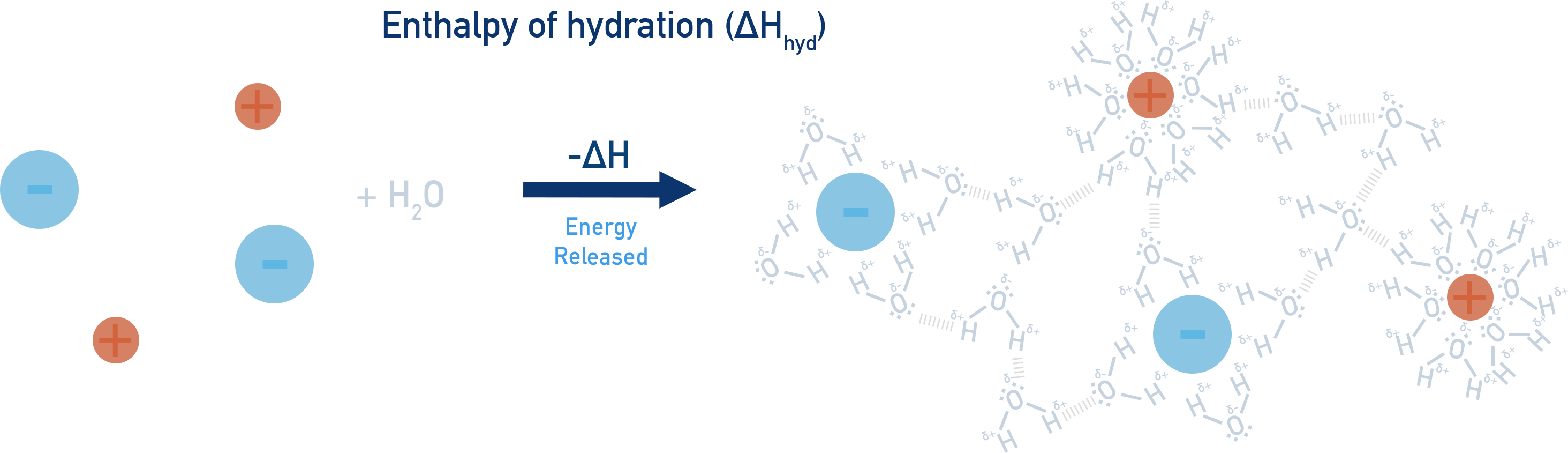
Example

Na⁺(g) → Na⁺(aq)
Cl⁻(g) → Cl⁻(aq)

Energy Cycle for Solution Enthalpy

An energy cycle can be constructed that links enthalpy of solution (ΔH_sol), hydration enthalpies (ΔH_hyd) and lattice energy (ΔH_latt):

Matt’s exam tip

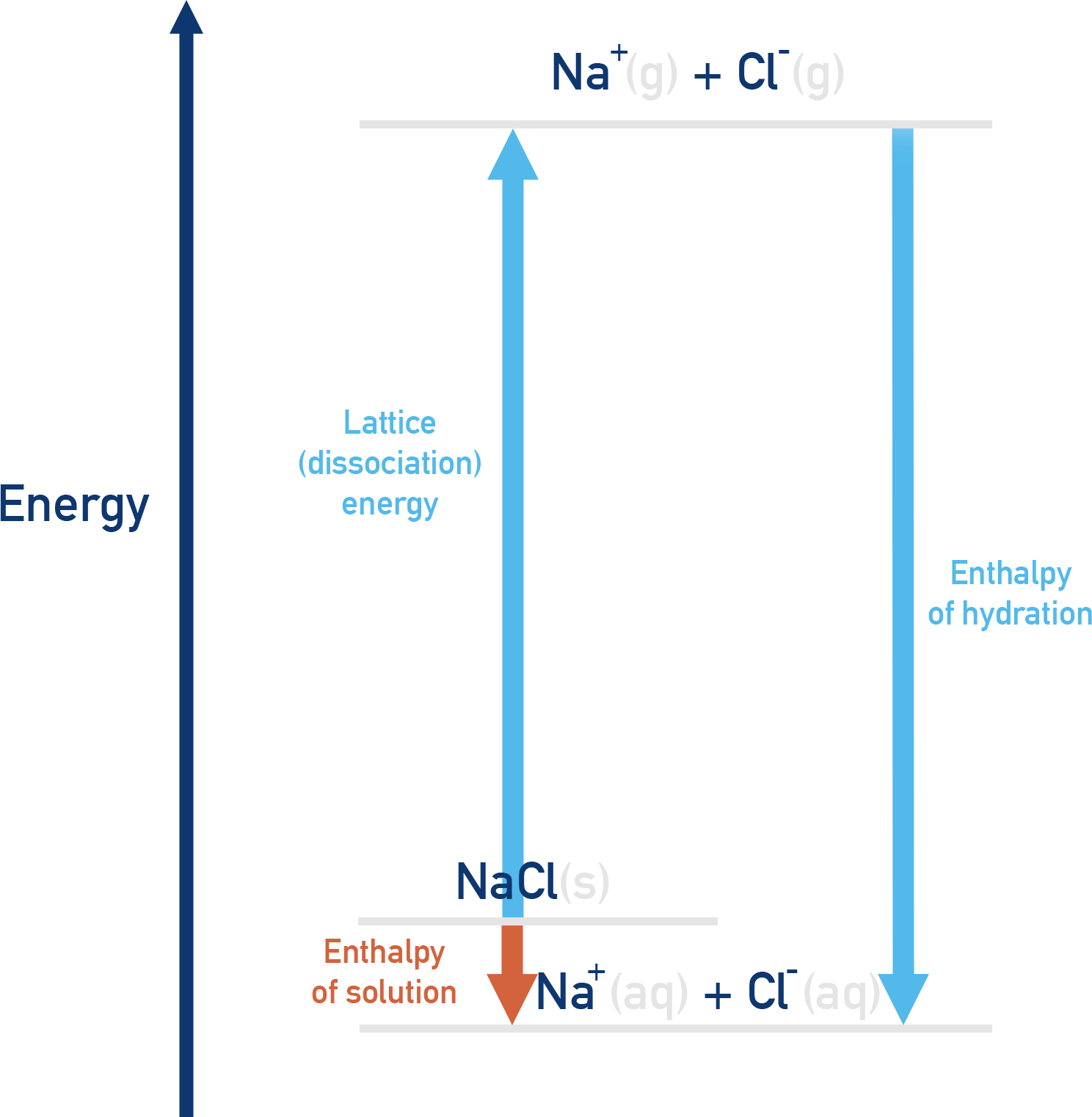
For these energy cycles, the lattice energy is given as a positive value as the arrow direction is going from the ionic solid to the gaseous ions, this is breaking apart the lattice. This is the exact same value as lattice energy however it has a positive sign (+ΔH) rather than negative as it is an endothermic process.

Energy cycle equation:

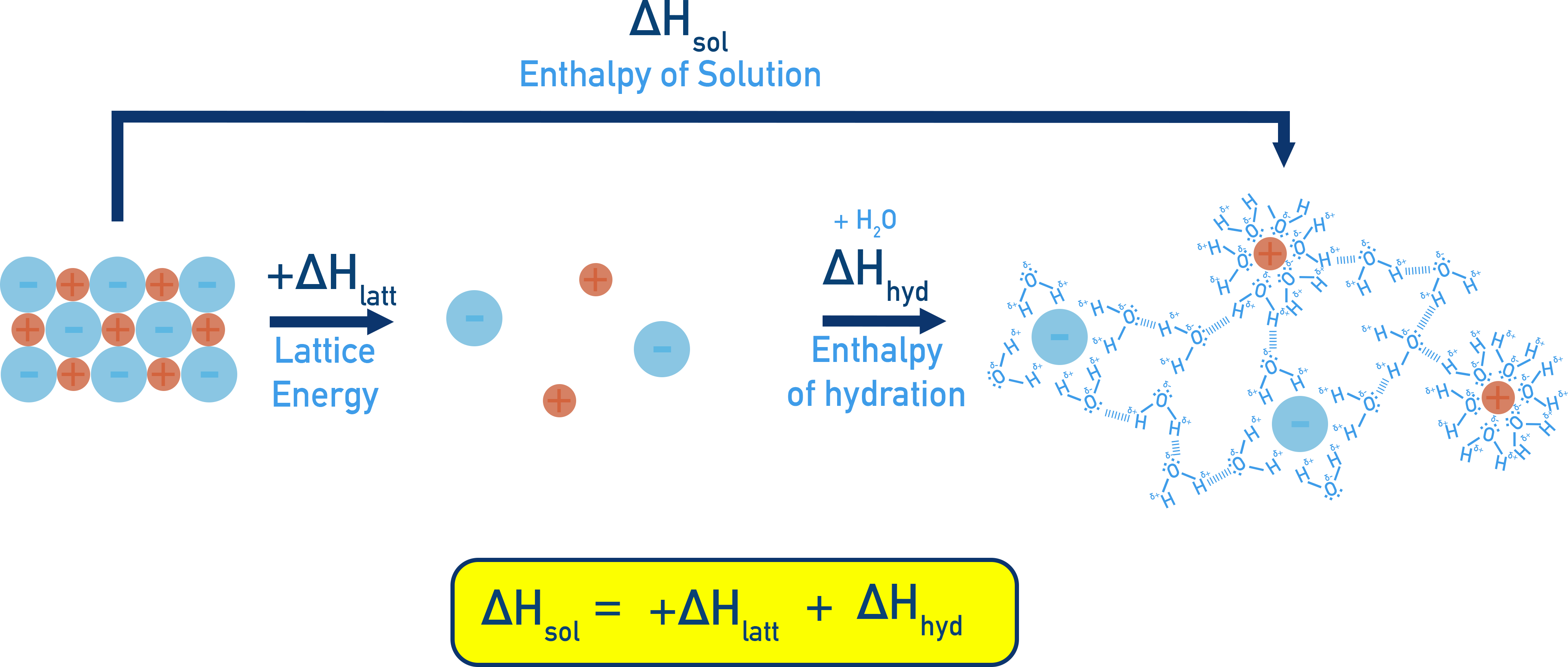
• ΔH_latt is positive (energy needed to break lattice).
• ΔH_hyd is negative (energy released when ions are hydrated).

Factors Affecting Enthalpy of Hydration

The magnitude of ΔH_hyd depends on:

• Ionic charge:
  Higher charge = stronger attraction to water = more exothermic ΔH_hyd.
  Example Mg²⁺ has more negative ΔH_hyd than Na⁺.
• Ionic radius:
  Smaller ions = stronger electrostatic attraction to water = more exothermic ΔH_hyd.
  Example Li⁺ is more exothermic than Cs⁺.

So, small, highly charged ions have more exothermic hydration enthalpies.

Summary

• Lattice energy is the energy released when 1 mole of an ionic solid forms from gaseous ions.
• Born–Haber cycles are used to calculate lattice energies from experimental data.
• Factors affecting lattice enthalpy: ionic charge and ionic radius.
• Difference between experimental and theoretical values suggests covalent character.
• Polarising power of cations and polarisability of anions introduce covalent character.
• Enthalpy of solution = lattice energy + hydration enthalpies.
• Hydration enthalpies are more exothermic for small, highly charged ions.