Relative Masses and Mass Spectrometry

Specification Reference Topic 1, points 7–10 (Edexcel A-Level Chemistry)

Quick Notes

Relative Molecular Mass (M_r):
- The sum of the relative atomic masses (A_r) of all atoms in a molecule.
- Calculate using A_r values from the periodic table.
Relative Formula Mass:
- Used for giant structures (e.g., ionic compounds).
- Calculated in the same way as M_r, using A_r values.
Mass Spectrometry: Relative Atomic Mass:
- Mass spectrometry provides m/z values and relative abundances.
- Use the formula:
  A_r = (Σ (isotopic mass × % abundance)) ÷ 100
Mass Spectra of Diatomic Molecules:
- Molecules like Cl₂ show multiple peaks.
- Peaks arise from different isotope combinations:
  e.g. Cl-35 + Cl-35, Cl-35 + Cl-37, Cl-37 + Cl-37.
- Peak heights depend on the probabilities of these combinations:
  Typically, 35–35 > 35–37 > 37–37.
Relative Molecular Mass from Mass Spectrometry:
- The highest m/z peak (M⁺) gives the M_r of the molecule.
- M⁺ peak represents the molecular ion: the whole molecule with one electron removed.

Full Notes

Mass number, isotopes and mass spectrometry have been outlined in more detail here, here and here.
This page is just what you need to know for Edexcel A-level :)

Relative Molecular Mass (M_r)

The relative molecular mass (M_r) of a molecule is the sum of the relative atomic masses (A_r) of all atoms in the molecule.

Example M_r of Water (H₂O)

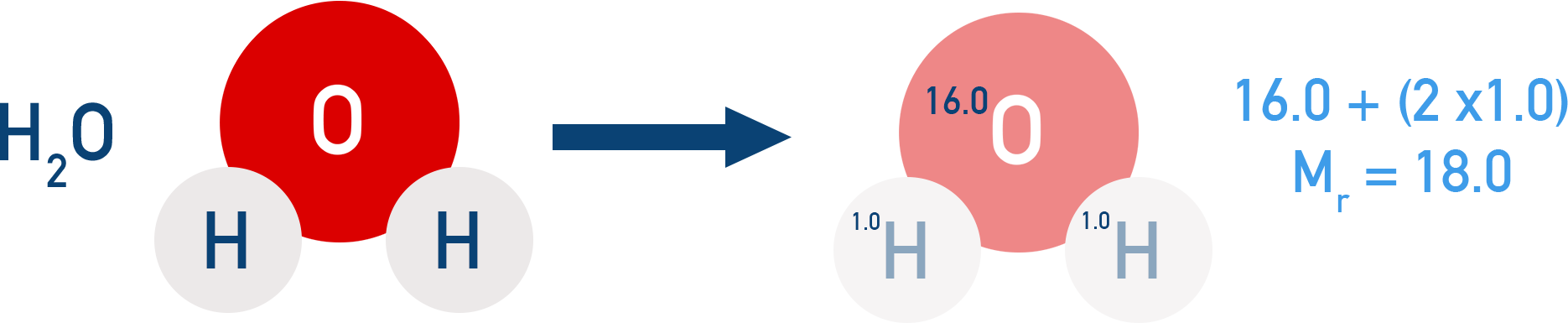
Edexcel A-Level Chemistry worked example showing calculation of Mᵣ for water H₂O using Aᵣ(H)=1.0 and Aᵣ(O)=16.0 to give Mᵣ=18.0.

Hydrogen A_r = 1.0
Oxygen A_r = 16.0
M_r = (2 × 1.0) + (1 × 16.0) = 18.0

Relative Formula Mass

Relative formula mass is used for compounds with giant structures, such as ionic lattices or metals.

It is calculated the same way as M_r, but it refers to a formula unit, not a discrete molecule.

Example Sodium chloride (NaCl)

NaCl = 23.0 (Na) + 35.5 (Cl) = 58.5

Relative Atomic Mass from Mass Spectrometry

A mass spectrum shows:

m/z values (mass-to-charge ratio).
Peak height or area corresponds to relative abundance.

For elements, the spectrum shows different isotopes. For molecules, a peak with the highest m/z represents the molecular ion (M⁺).

Calculating Relative Atomic Mass (A_r)

We can calculate A_r using this formula:

A_r = (Σ (isotopic mass × % abundance)) / 100

Example Chlorine

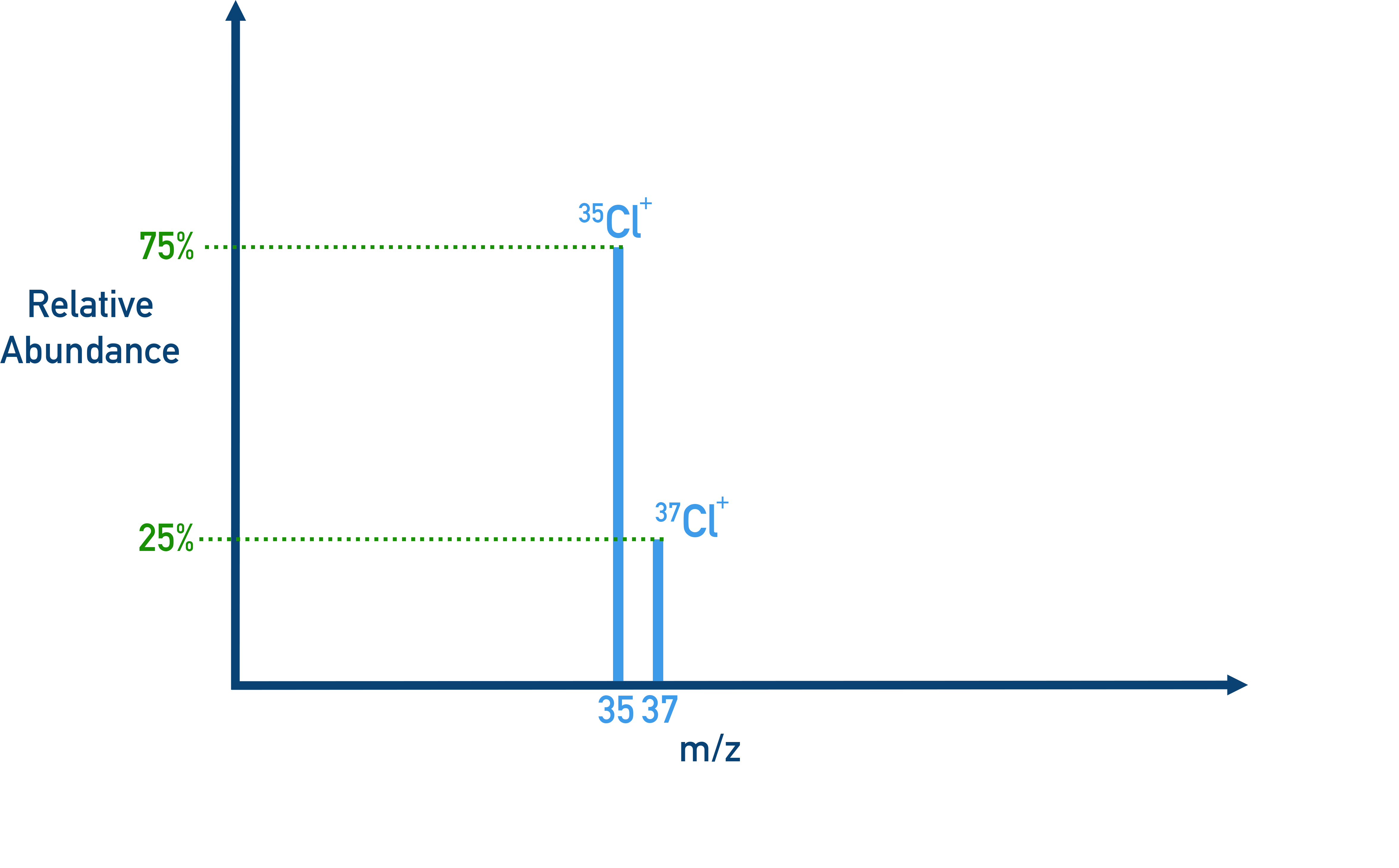
Edexcel A-Level Chemistry mass spectrum of chlorine showing Cl-35 and Cl-37 isotope peaks used to calculate Aᵣ = 35.5.

Cl-35 (75%)
Cl-37 (25%)
A_r = (35 × 75 + 37 × 25) / 100 = 35.5

Mass Spectra of Diatomic Molecules

Diatomic molecules like Cl₂ can produce a more complex spectrum.

This is because there are several possible combinations of isotopes within the molecule.

For example, with Cl₂, Chlorine has two common isotopes:

Cl-35 has a relative abundance of 75% (¾)
Cl-37 has a relative abundance of 25% (¼)

There are three possible combinations of Cl isotopes in a Cl₂ molecule, giving three molecular ion peaks in a mass spectra.

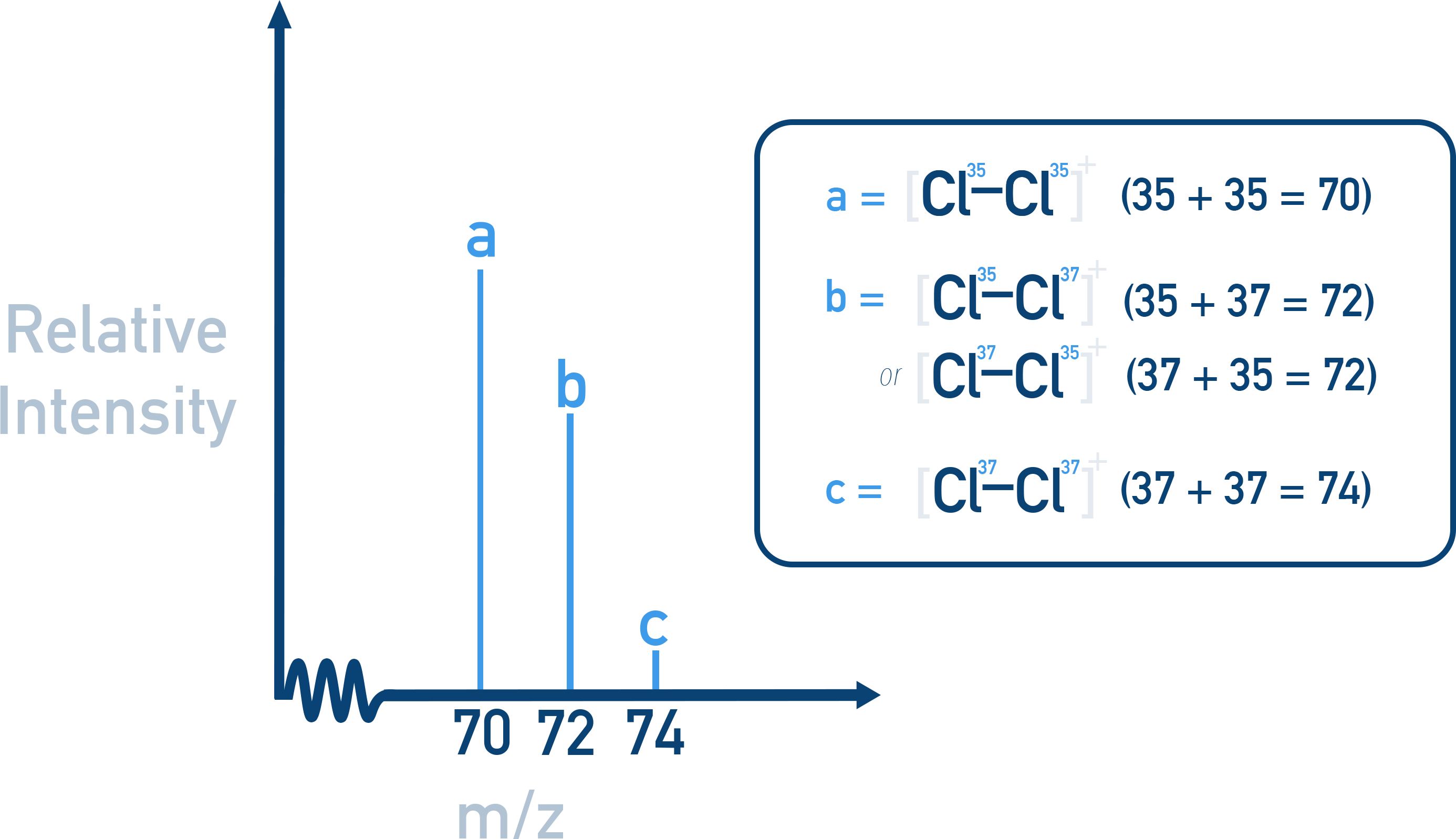
Edexcel A-Level Chemistry mass spectrum for Cl₂ showing three molecular ion peaks at m/z 70, 72 and 74 from 35–35, 35–37 and 37–37 isotope combinations.

35-35 → m/z = 70
35-37 → m/z = 72
37-37 → m/z = 74

Peak intensities (heights) reflect probability of each isotope combination.

For example, in Cl₂, the m/z = 70 peak is the tallest due to the high abundance of Cl-35 and the ratio of each peak height is 9 : 6 : 1

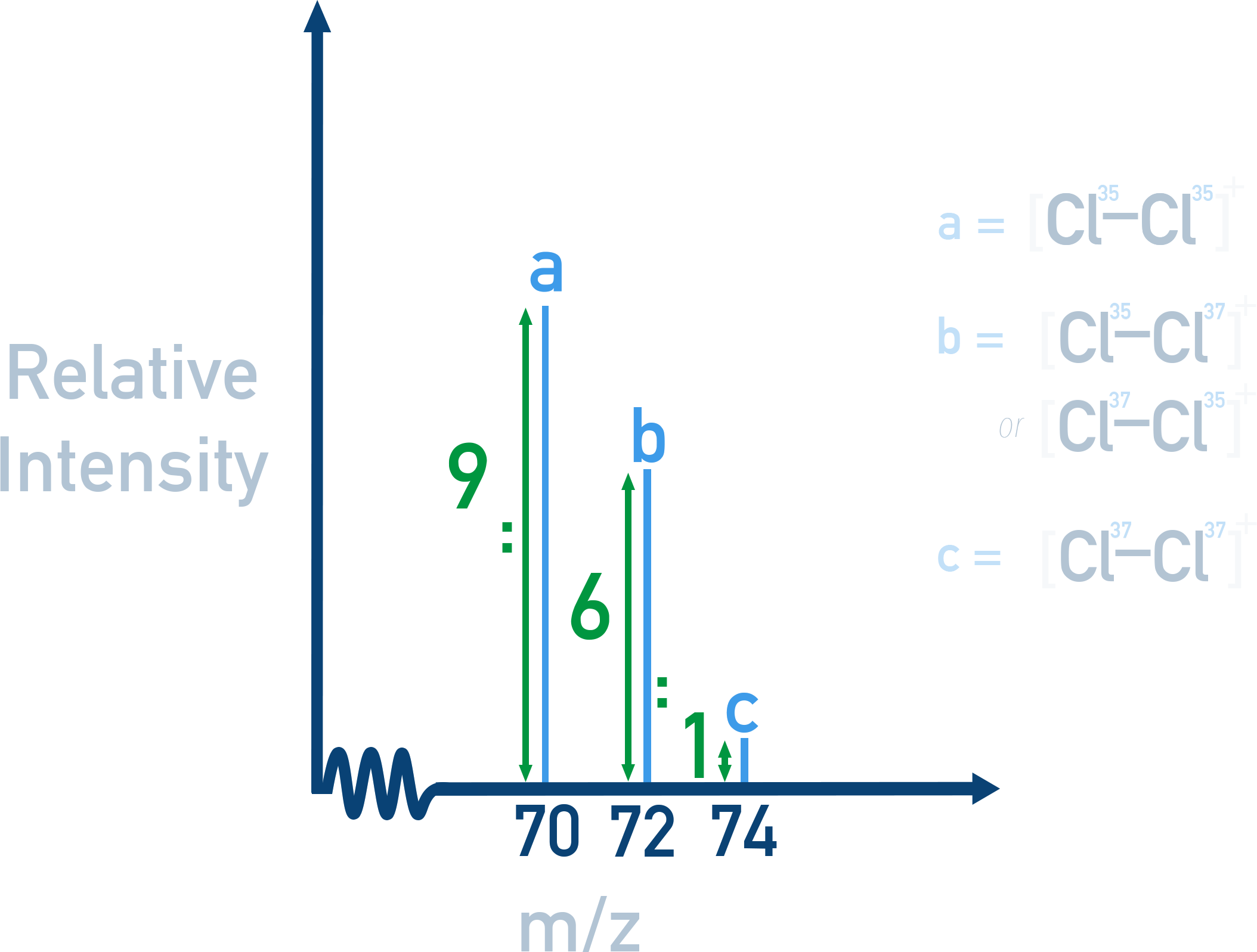
Edexcel A-Level Chemistry diagram showing Cl₂ molecular ion peak height ratio 9:6:1 for m/z 70, 72 and 74 based on isotope probabilities.

This is because of each possible isotope combinations and the probability of each occurring:

Cl-35 + Cl-35 → m/z = 70
Probability = ¾ × ¾ = 9/16

Cl-35 + Cl-37 → m/z = 72
Probability = ¾ × ¼ = 3/16

Cl-37 + Cl-35 → m/z = 72
Probability = ¼ × ¾ = 3/16

(This is the same molecule as above, so their probabilities add)
Total probability for m/z 72 = 3/16 + 3/16 = 6/16

Cl-37 + Cl-37 → m/z = 74
Probability = ¼ × ¼ = 1/16

Resulting peak intensities:
m/z = 70 → 9/16
m/z = 72 → 6/16
m/z = 74 → 1/16

Peak height ratio in the mass spectrum: 9 : 6 : 1

Why this matters:
Being able to predict the pattern helps identify diatomic molecules and confirms the presence of elements with multiple isotopes like chlorine.

Matt’s exam tip

If asked to show why a Cl₂ sample has a peak height ratio of 9 : 6 : 1 in its mass spectra, answer using the fraction calculations as shown above. You don’t need to write lots of sentences. Just state that Cl has two isotopes, give each natural abundance (75% and 25%) and then show the fractions of probability for each pairing (as outlined above).

Determining Relative Molecular Mass from Mass Spectra

The relative molecular mass of a molecule can be found from the M⁺ peak in a mass spectrum.

The M⁺ peak is the peak with the highest m/z (excluding isotope peaks) and shows the molecular mass of the compound.

Example Interpreting an M⁺ peak

If M⁺ is at m/z = 60, the molecular mass is 60.

The molecular ion peak (M⁺) has the highest m/z value.
Use precise atomic masses to confirm the molecular formula.

Example Determining the molecular formula with M⁺ = 58.12

Use the exact masses and likely formulae to match an M⁺ close to 58.12.

Edexcel A-Level Chemistry example graphic for identifying a molecular formula C4H10 from an M⁺ peak at 58.12 using precise atomic masses.

Summary

M_r is the sum of A_r values for atoms in a molecule and relative formula mass applies to formula units in giant structures.
Mass spectra show m/z and relative abundance. We can use them to calculate A_r with the weighted average formula.
Diatomic molecules like Cl₂ give multiple M⁺ peaks whose heights follow probabilities, giving 9 : 6 : 1 for chlorine.
The molecular ion peak M⁺ gives the molecule’s M_r we can use precise masses to confirm the formula.