Core Practical 8: Enthalpy Change and Hess’s Law

Aim: To calculate the molar enthalpy changes of two reactions involving potassium carbonate and potassium hydrogencarbonate, and use Hess’s Law to determine the enthalpy change for the thermal decomposition of KHCO₃.

Key Concepts

You will carry out two reactions:

Reaction 1 – Potassium carbonate with HCl:
K₂CO₃(s) + 2HCl(aq) → 2KCl(aq) + CO₂(g) + H₂O(l)

Reaction 2 – Potassium hydrogencarbonate with HCl:
KHCO₃(s) + HCl(aq) → KCl(aq) + CO₂(g) + H₂O(l)

Target Reaction (Reaction 3) – Thermal decomposition:
2KHCO₃(s) → K₂CO₃(s) + CO₂(g) + H₂O(l)

You’ll use Hess’s Law:
ΔH₃ = ΔH₁ – 2 × ΔH₂

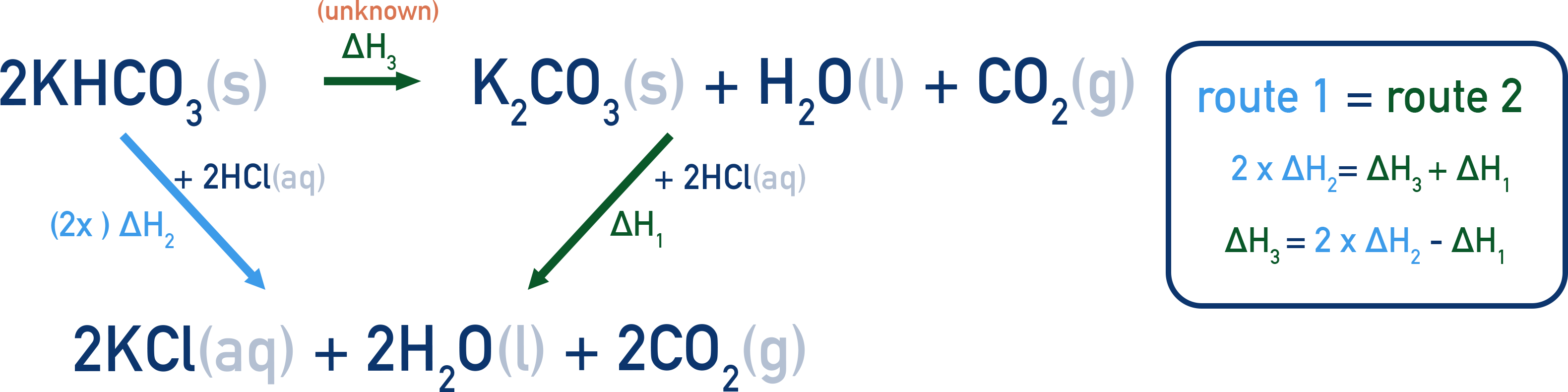
Safety

Wear goggles.
2 mol dm⁻³ HCl is an irritant.
Potassium carbonate is also an irritant.

Apparatus and Chemicals

Apparatus

Test tubes
Polystyrene cup
250 cm³ or 400 cm³ beaker
Thermometer (up to 50 °C)
Burette, clamp, and stand
Mass balance (2 d.p.), stirring rod, spatula

Chemicals

2 mol dm⁻³ hydrochloric acid (~60 cm³)
Potassium carbonate (3.0 g, anhydrous)
Potassium hydrogencarbonate (3.5 g)

Procedure

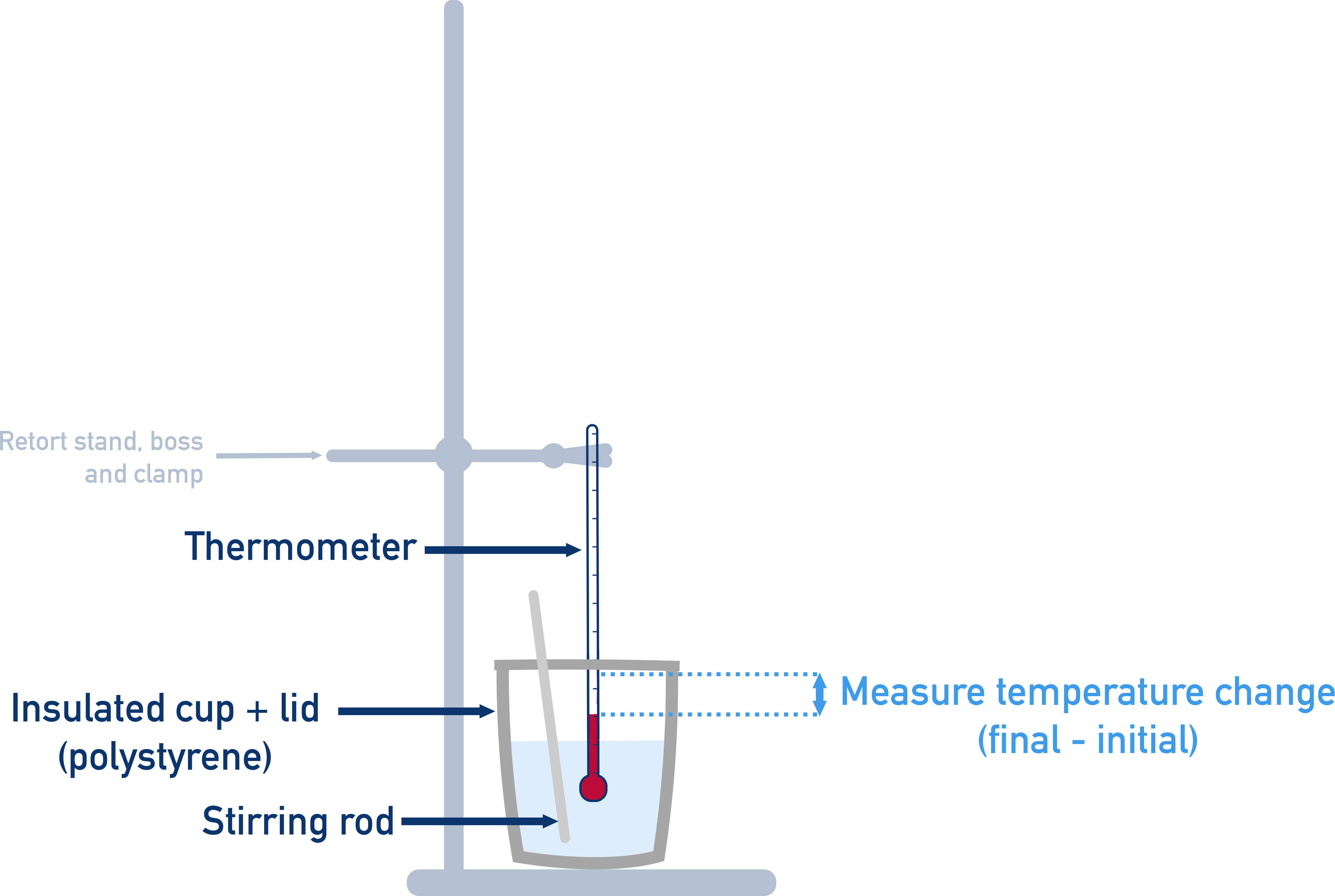
Edexcel A-Level Chemistry calorimetry setup using a polystyrene cup for measuring enthalpy change.

Part A – K₂CO₃ Reaction

Weigh test tube + approx. 3.0 g potassium carbonate.
Use a burette to place 30 cm³ of HCl into a polystyrene cup.
Record starting temperature.
Add carbonate, stir, record highest temperature.
Reweigh empty test tube to find mass used.

Part B – KHCO₃ Reaction

Repeat steps using ~3.5 g potassium hydrogencarbonate.
This time, record the lowest temperature reached.

Sample Data

Solid	Mass used (g)	Temperature change (°C)
Potassium carbonate (K₂CO₃)	2.08	+5.2
Potassium hydrogencarbonate (KHCO₃)	3.33	–3.9

Calculations

Step 1 – Calculate energy change (q)
q = mcΔT (Assume mass = 30 g; c = 4.2 J g⁻¹ °C⁻¹)

K₂CO₃: q = 30 × 4.2 × 5.2 = 655.2 J
KHCO₃: q = 30 × 4.2 × 3.9 = 491.4 J

Step 2 – Moles

K₂CO₃ (M_r = 138.2): 2.08 ÷ 138.2 = 0.015 mol
KHCO₃ (M_r = 100.1): 3.33 ÷ 100.1 = 0.033 mol

Step 3 – Enthalpy change per mole (ΔH)
ΔH = q ÷ mol (convert q to kJ)

K₂CO₃: –0.655 kJ ÷ 0.015 mol = –43.7 kJ mol⁻¹
KHCO₃: –0.491 kJ ÷ 0.033 mol = –14.9 kJ mol⁻¹

Step 4 – Apply Hess’s Law
ΔH₃ = ΔH₁ – 2 × ΔH₂
ΔH₃ = –43.7 – (2 × –14.9) = –43.7 + 29.8 = –13.9 kJ mol⁻¹

Matt’s exam tip

Specific heat capacity of solution is assumed to be the same as water (4.2 J g⁻¹ °C⁻¹). ΔH is negative for exothermic, positive for endothermic. Always show clear working for mole and energy calculations.