Ideal Gases

Full Notes

The behavior of gases can be described using the ideal gas law, which relates pressure, volume, temperature, and number of moles. Although no gas is truly ideal, most gases behave nearly ideally under many conditions.

What Is an Ideal Gas?

An ideal gas is a simplified model used in chemistry to help us understand and calculate gas behavior.

Real gases only approximate ideal behavior under normal conditions (room temperature and pressure), but the model itself is based on a set of assumptions.

These assumptions enable us to consider that only temperature, pressure and moles of a gas determine the volume occupied and we can ignore the type of gas it is.

Key Assumptions of the Ideal Gas Model

To behave as an ideal gas, a substance must meet these assumptions:

• Particles are in constant, random motion
  They move freely in straight lines until they collide with other particles or the container walls.


• The volume of individual gas particles is negligible
  The size of the gas particles is so small that their total volume is effectively zero compared to the container.


• No intermolecular forces exist
  There are no attractions or repulsions between gas particles. They do not interact except during collisions.


• All collisions are elastic
  When gas particles collide, they do not lose kinetic energy. The total kinetic energy before and after a collision is the same.


• Temperature is related to average kinetic energy
  The higher the temperature, the faster the particles move.
  
  All particles have different kinetic energies, but the average increases with temperature.

Real vs Ideal Gases

Real gases behave nearly ideally under high temperature and low pressure.

At low temperatures or high pressures, real gases deviate because:

• At high pressures, gas particles occupy space, meaning their volume is no longer negligible.

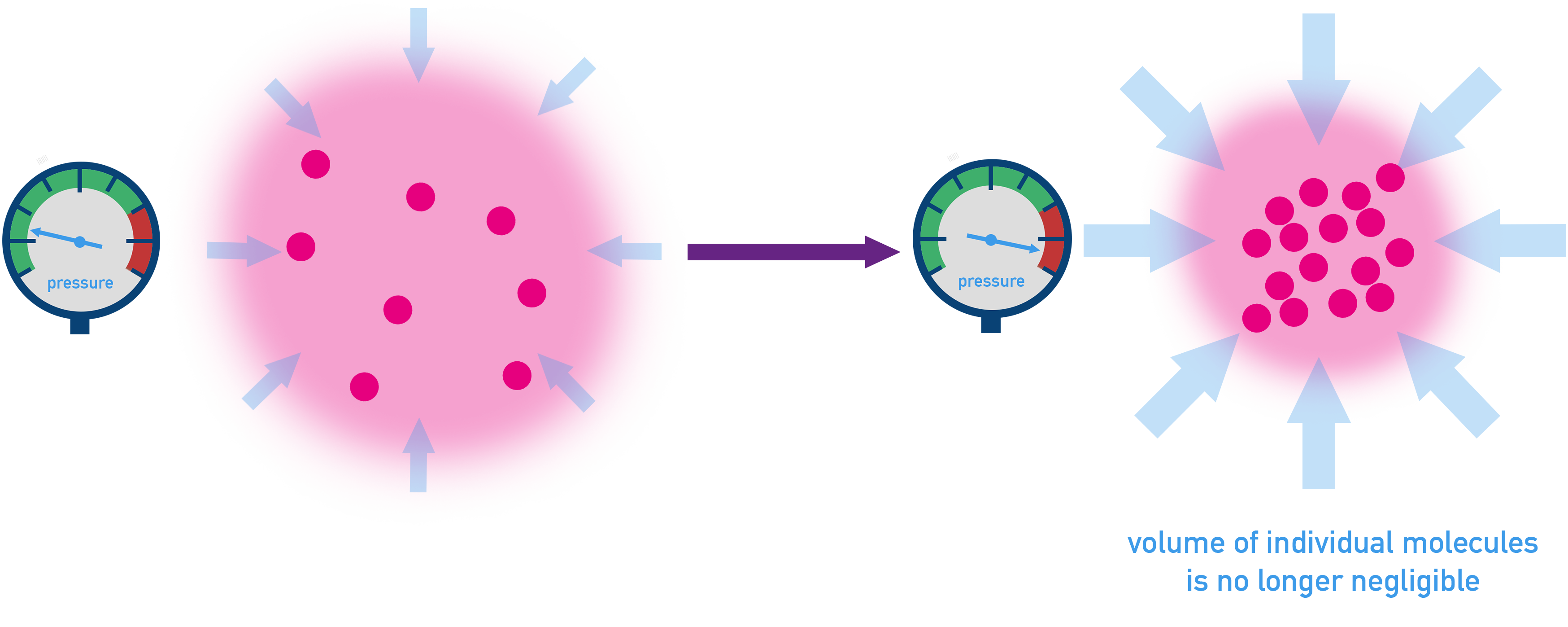
• At low temperatures, intermolecular forces become significant, making gases more likely to condense.

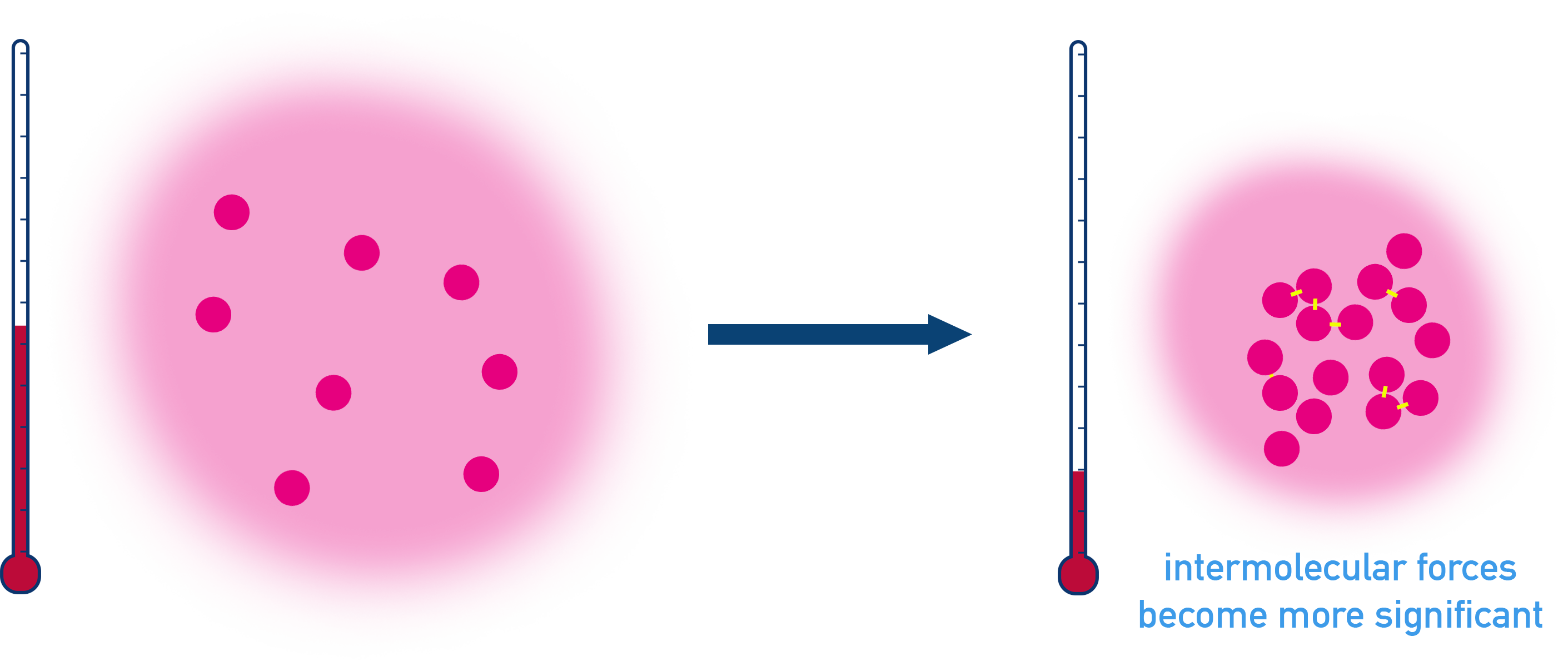
The Ideal Gas Law

Equation:

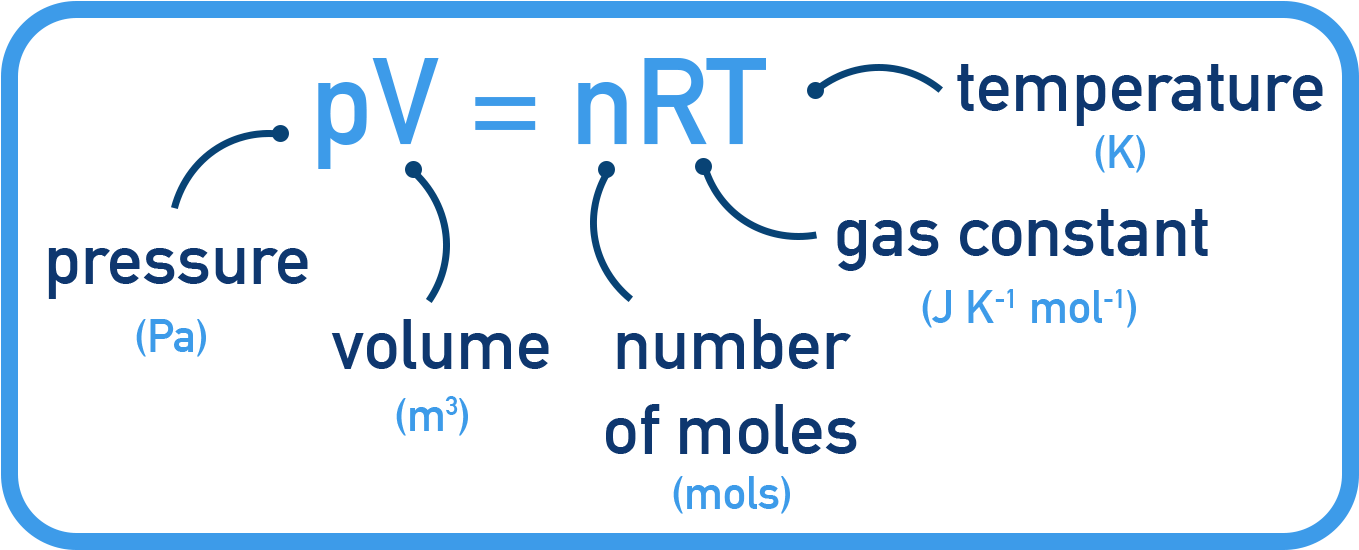
PV = nRT

Where:
P = pressure (in atmospheres)
V = volume (in liters)
n = moles of gas
R = gas constant = 0.0821 L·atm/mol·K
T = temperature (in kelvin)

Key points:

• Always use kelvin for temperature: K = °C + 273
• Use liters for volume and atm for pressure unless R is adjusted
• Rearranged forms are useful depending on the variable you’re solving for:
  V = nRT / P
  T = PV / nR
  n = PV / RT

Partial Pressure and Gas Mixtures

In mixtures of gases, each gas contributes to the total pressure independently. This is called Dalton’s Law of Partial Pressures.

Key equations:
P_total = P_A + P_B + P_C + ...
Mole fraction: X_A = moles of A / total moles
Partial pressure: P_A = X_A × P_total

Each gas’s partial pressure depends only on:

• Its mole fraction
• The total pressure of the system

Graphical Representations of Gas Relationships

Common graphs:

P vs. V (at constant T)

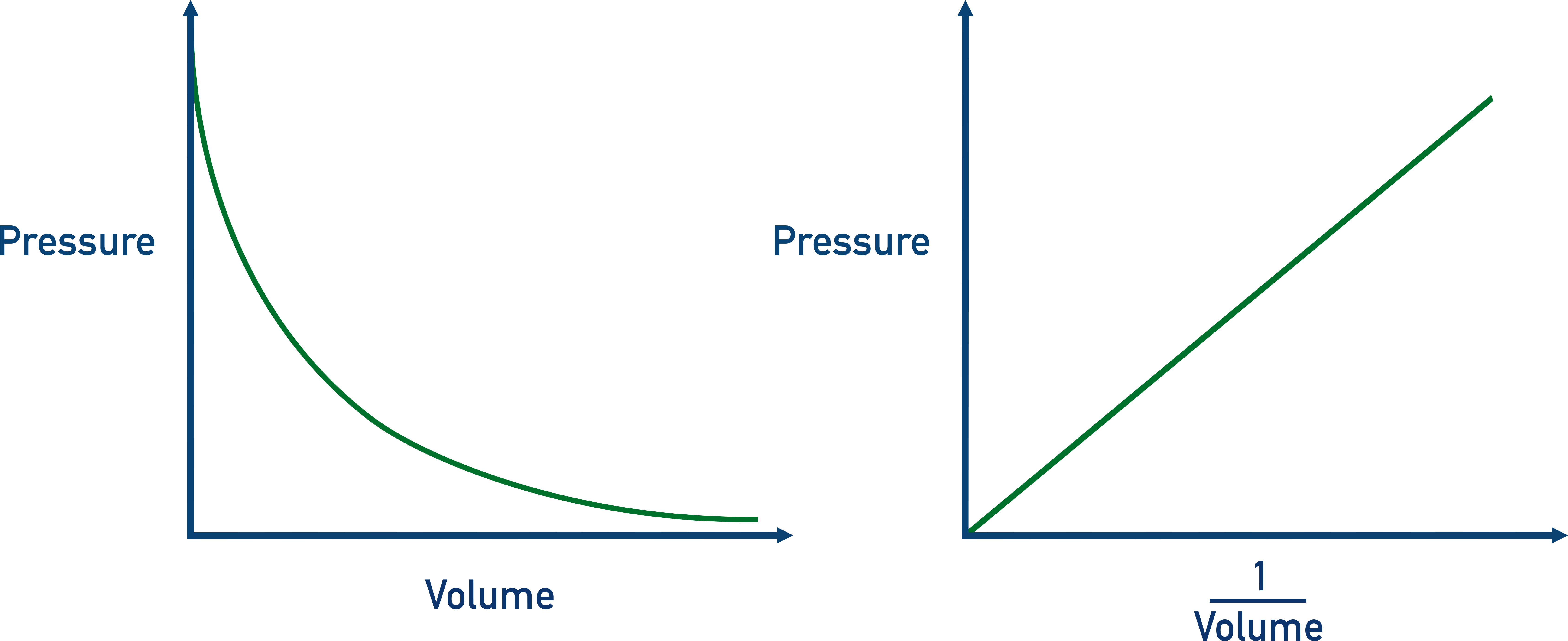
Inverse relationship (Boyle’s Law)
As volume increases, pressure decreases

V vs. T (at constant P)

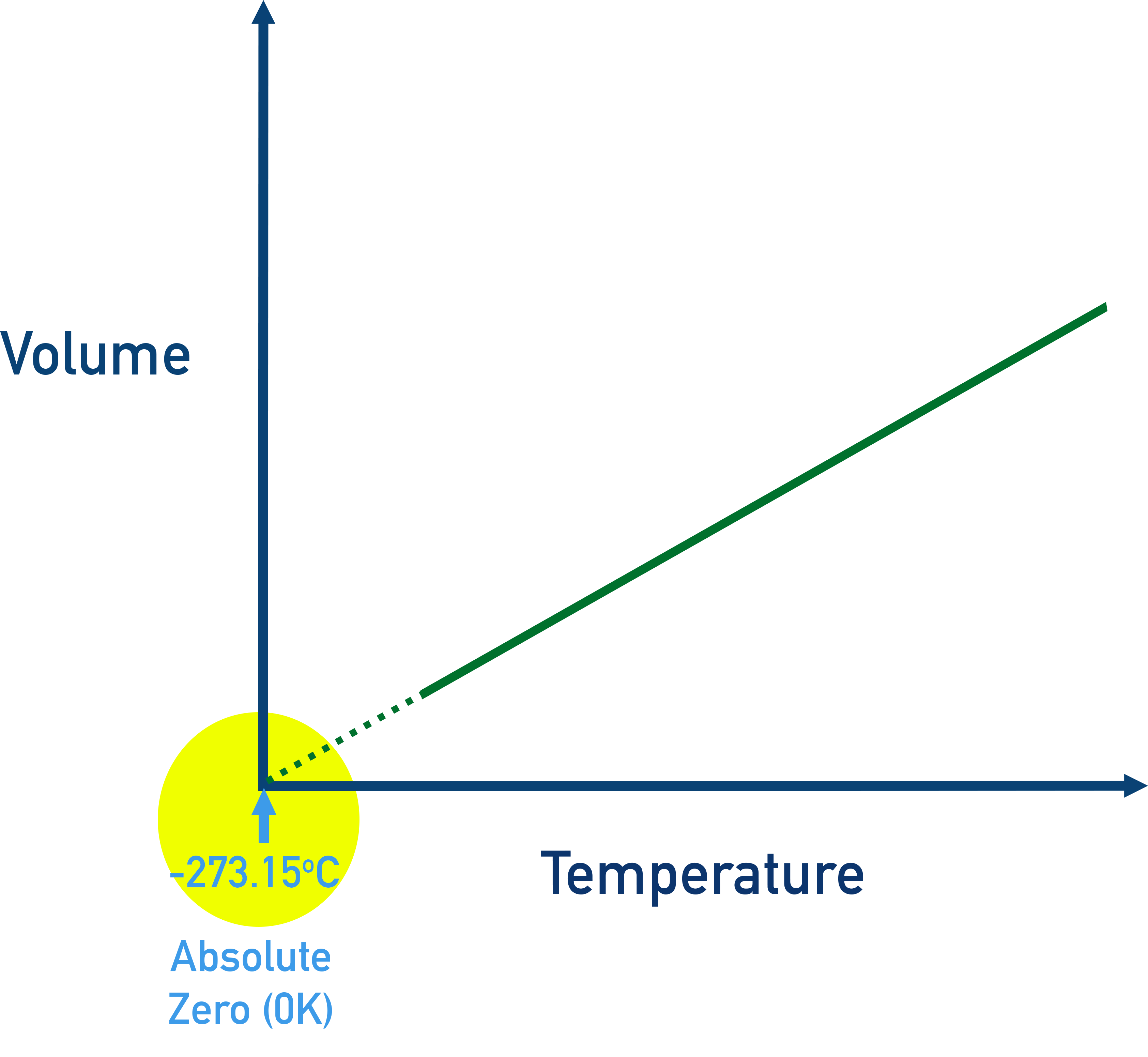
Direct relationship (Charles’s Law)
As temperature increases, volume increases

P vs. T (at constant V)

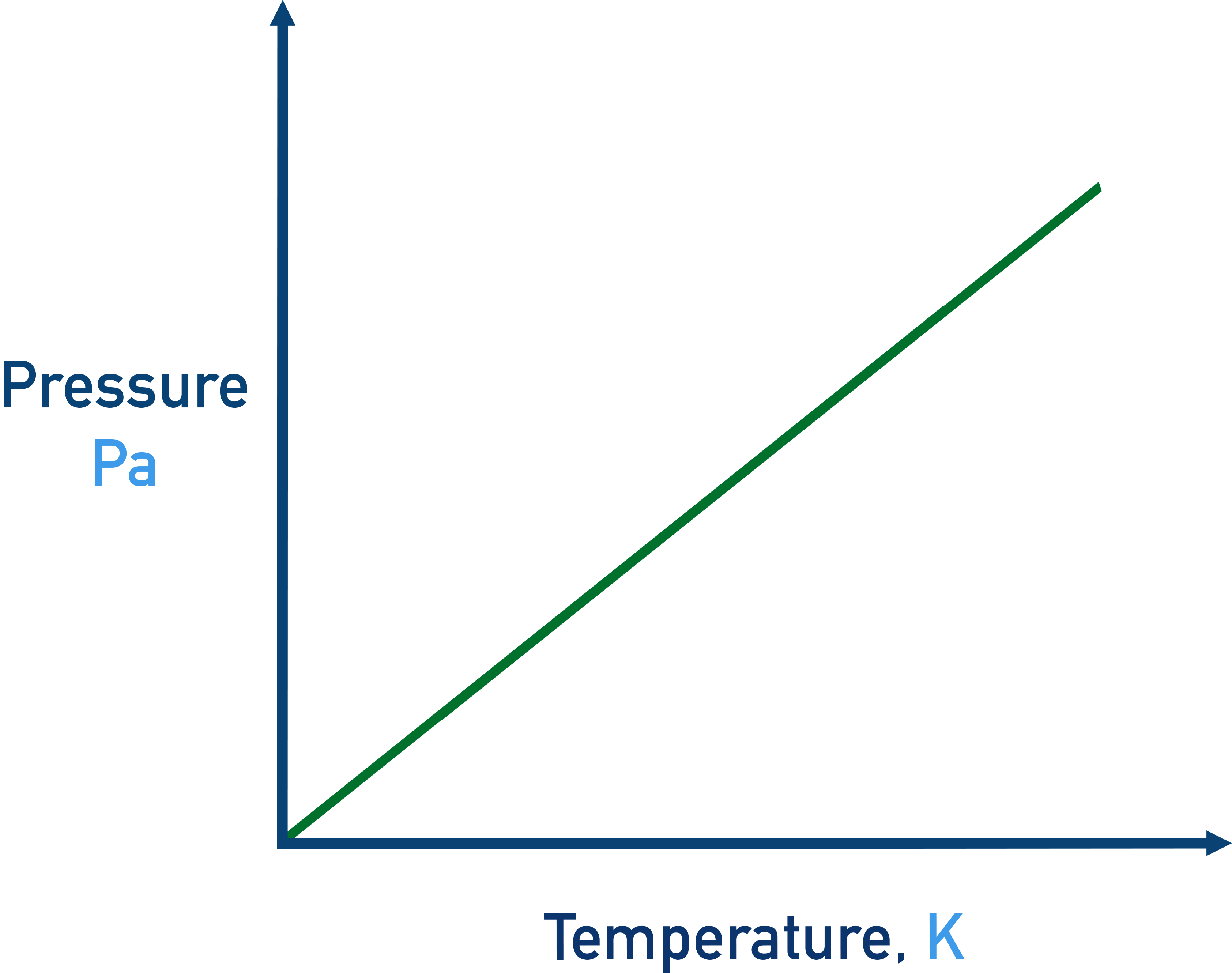
Direct relationship (Gay-Lussac’s Law)
As temperature increases, pressure increases

V vs. n (at constant T and P)

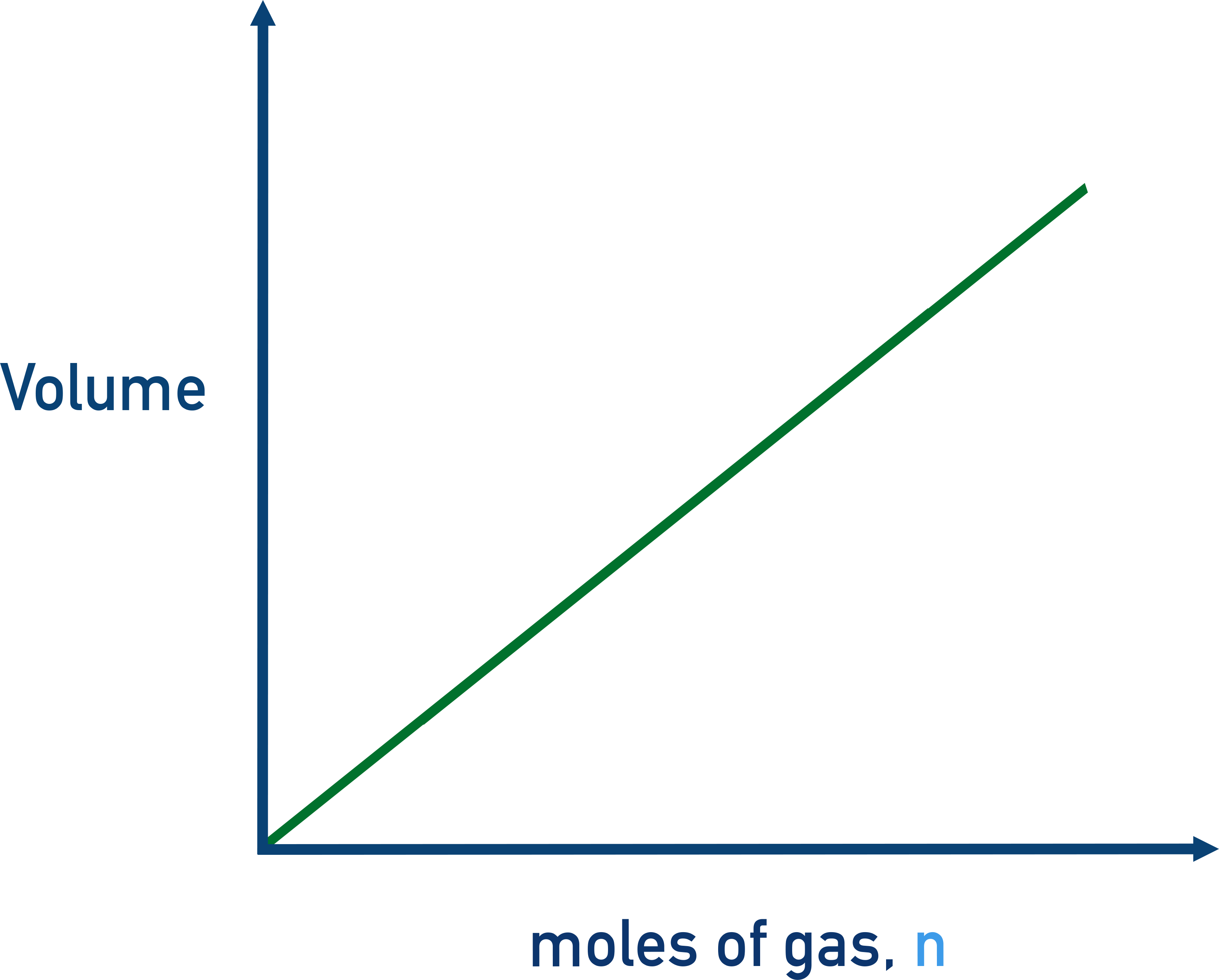
Direct relationship (Avogadro’s Law)
More moles = greater volume

These relationships can be explained by kinetic molecular theory, which models gas behavior at the particle level.

Matt’s exam tip

If a question involves gas mixtures, always calculate mole fractions before partial pressures. Don’t forget to convert Celsius to Kelvin, and check your R units match the question.

Summary

The ideal gas law allows us to predict how gases behave by connecting four variables: pressure, volume, temperature, and moles. In gas mixtures, Dalton’s Law tells us that each gas contributes to the total pressure independently. The use of mole fraction and partial pressure is essential when working with multiple gases. These relationships are often visualized with graphs and understood through the kinetic molecular model of gases.

Key equations:
PV = nRT
P_total = P_A + P_B + P_C + ...
X_A = moles A / total moles
P_A = X_A × P_total