Properties of Photons

Learning Objective 3.12.A Explain the properties of an absorbed or emitted photon in relationship to an electronic transition in an atom or molecule.

Quick Notes

When a photon is absorbed, an atom or molecule gains energy and may undergo an electronic transition to a higher energy level.
When a photon is emitted, the atom or molecule loses energy as the electron drops to a lower energy level.
Photon energy (E) is related to its frequency (f) by Planck’s equation:

E = h × f
Where E is Energy, h is Planck's constant and f is frequency

Wavelength (λ) and frequency are related to the speed of light (c) by the equation:

c = λ × f
Where c is speed of light, λ is wavelength and f is frequency

Note that freqency is also shown as v in equations

Full Notes

Photons are packets of electromagnetic energy. When atoms or molecules absorb or emit photons, electrons can transition between different energy levels.

Energy Transitions and Photons

AP Chemistry diagram showing photon absorption raising an electron to an excited state, and photon emission when it drops back to the ground state.

If a photon is absorbed, the energy of the atom or molecule increases, and an electron moves to a higher energy level.
If a photon is emitted, the energy of the atom or molecule decreases, and an electron falls to a lower energy level.

The amount of energy absorbed or released corresponds exactly to the energy of the photon.

Planck’s Equation – Photon Energy

The energy of a photon is directly proportional to its frequency:

AP Chemistry formula diagram showing Planck’s equation, E = h × v, with variables defined.

E = h × v

E = energy of the photon (in joules)
h = Planck’s constant (6.626 × 10^-34 J·s)
v = frequency of the electromagnetic wave (in s^-1)

Speed of Light and Wavelength

The frequency of a wave is related to its wavelength (λ) and the speed of light (c):

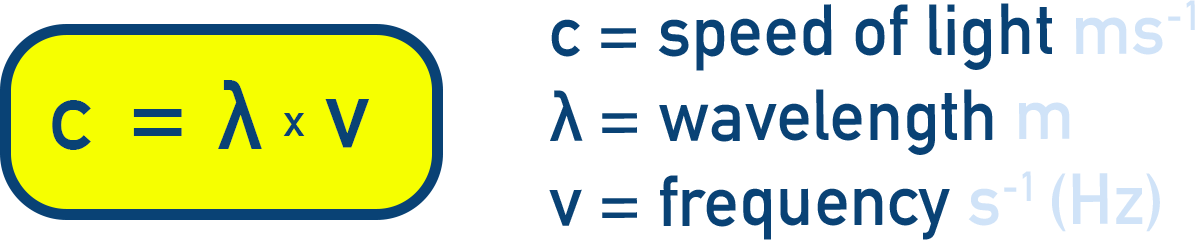
c = λ × v

c = speed of light (3.00 × 10⁸ m/s)
λ = wavelength (in meters)
v = frequency (in s^-1)

Using both equations together allows us to calculate the energy of a photon from either its frequency or wavelength.

Worked Example

Question: What is the energy of a photon with a wavelength of 400 nm?

Step 1: Convert wavelength to meters
λ = 400 nm = 4.00 × 10^-7 m
Step 2: Use c = λ × f to find frequency
f = c ÷ λ = (3.00 × 10⁸ m/s) ÷ (4.00 × 10^-7 m) = 7.50 × 10¹⁴ s^-1
Step 3: Use Planck’s equation to find energy
E = h × f = (6.626 × 10^-34 J·s) × (7.50 × 10¹⁴ s^-1)
E = 4.97 × 10^-19 J

Answer: 4.97 × 10^-19 J

Matt’s exam tip

Always check your units when working with wavelength or frequency. If you’re given nm, convert to meters before using c = λ × f. Also remember that shorter wavelengths = higher energy photons.

Summary

Photons carry energy that can be absorbed or emitted by atoms and molecules during electronic transitions.
The energy of a photon (E) depends on its frequency (f): E = h × f
c = λ × f
These relationships allow us to calculate how much energy is transferred during absorption or emission.
Understanding these equations is essential for interpreting electronic transitions in spectroscopy.