Concentration Changes Over Time

Learning Objective 5.3.A Identify the rate law expression of a chemical reaction using data that show how the concentrations of reaction species change over time.

Quick Notes

Graphs of concentration vs. time help identify the order of a reaction.

Zeroth order: [A] vs. time is linear
First order: ln[A] vs. time is linear
Second order: 1/[A] vs. time is linear

The slope of the linear graph gives the rate constant, k.
Half-life (t_1/2) is constant only for first order reactions: t_1/2 = 0.693 / k
Radioactive decay is a classic example of first-order kinetics.

Full Notes

To understand how concentration changes over time, we monitor the concentration of a reactant, [A], during a reaction and look for patterns. The way the concentration of a reactant decreases over time depends on the reaction order with respect to the reactant.

Zeroth Order Reactions

Zeroth-order integrated rate law and linear [A] vs time plot with slope −k.

Rate is independent of [A]
Integrated rate law: [A]_t = [A]₀ − k t
Plot: [A] vs. time is linear with slope = −k
Units of k: mol·L⁻¹·s⁻¹

First Order Reactions

First-order integrated rate law and linear ln[A] vs time plot with slope −k.

Rate depends linearly on [A]
Integrated rate law: ln[A]_t = ln[A]₀ − k t
Plot: ln[A] vs. time is linear with slope = −k
Units of k: s⁻¹

Half-life is constant - see below: t_1/2 = 0.693 / k

Second Order Reactions

Second-order integrated rate law and linear 1/[A] vs time plot with slope +k.

Rate depends on [A]²
Integrated rate law: 1/[A]_t = 1/[A]₀ + k t
Plot: 1/[A] vs. time is linear with slope = +k
Units of k: L·mol⁻¹·s⁻¹

How to Identify the Order from Graphs

Plot [A] vs. time → Linear? Zeroth order
Plot ln[A] vs. time → Linear? First order
Plot 1/[A] vs. time → Linear? Second order

Whichever graph is linear tells you the order of the reaction. The slope of the line gives you the rate constant (k).

Half-Life and First Order Reactions

In first order reactions, the half-life (time for [A] to decrease to half) is constant, regardless of the starting concentration.

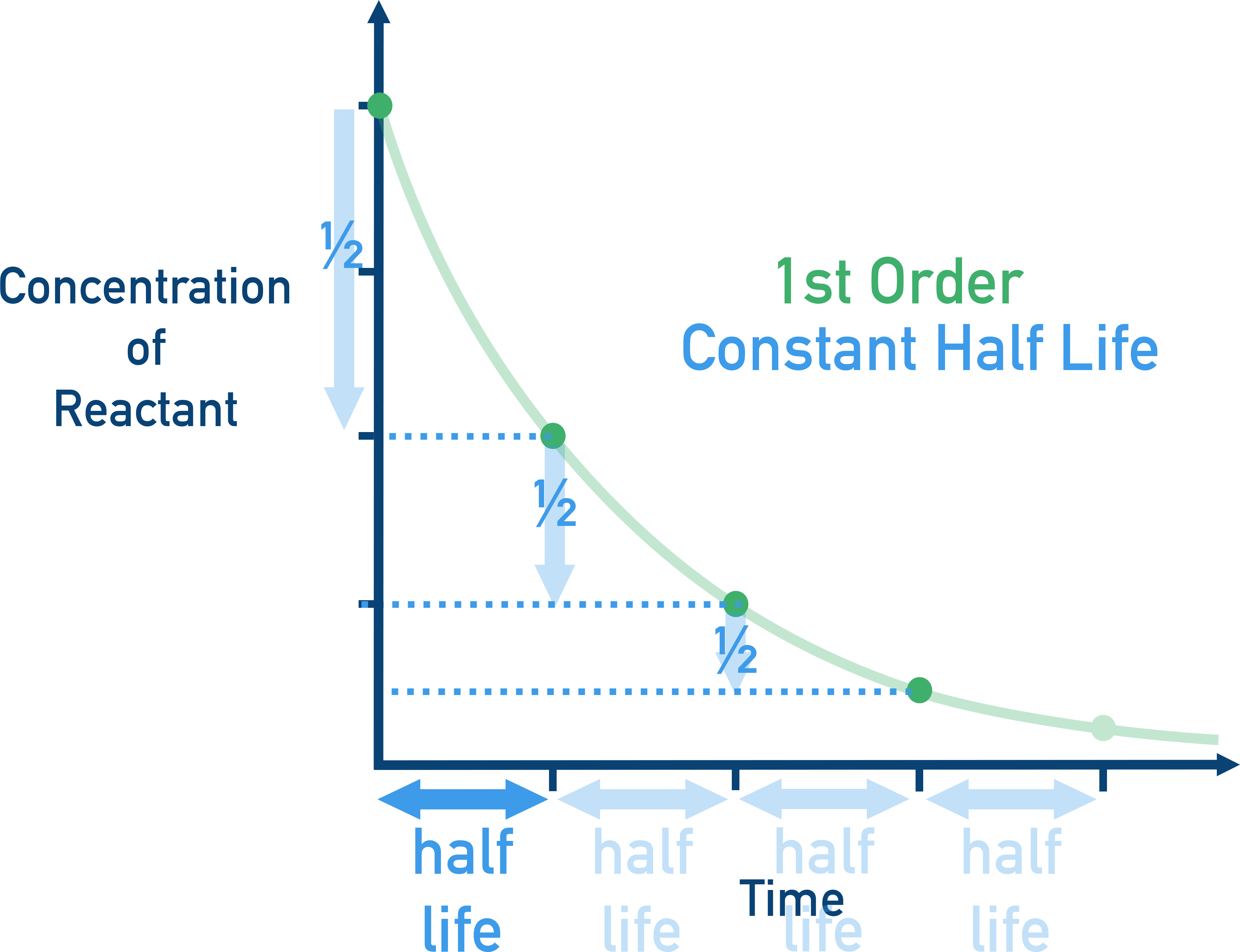
First-order decay curve showing constant half-life intervals.

Equation: t_1/2 = 0.693 / k.
This feature makes first order kinetics easy to identify and apply. It's also why first order equations are often used to model radioactive decay.

Example First-order decay with k = 0.010 s⁻¹:
t_1/2 = 0.693 / 0.010 = 69.3 s
the concentration halves every 69.3 seconds.

Matt’s exam tip

Make sure you know the three graphs and how to interpret them. If a question gives you time and concentration data, always try plotting ln[A] and 1/[A] to test for linearity — that tells you whether it’s first or second order.

Summary

Changes in reactant concentration over time allow us to determine the order of a reaction by analyzing different graphs.
Each order has a unique linear form and equation.
For first order reactions, half-life is a key feature and remains constant.

These principles help us determine rate laws from time-course data and apply them to real-world processes like radioactive decay.