Gases & Kinetic Molecular Theory

Learning Objective 3.5.A Explain the relationship between the motion of particles and the macroscopic properties of gases with: a. The kinetic molecular theory (KMT) b. A particulate model c. A graphical representation

Quick Notes

Kinetic Molecular Theory (KMT) explains how gas behavior results from the motion of particles.
Gas particles are in constant, random motion and collisions are elastic. We also assume the volume of individual particles is negligible.
The average kinetic energy (KE) of a gas particle depends only on temperature, not mass.

KE = ½m v²
heavier particles move more slowly at the same temperature.

Kelvin temperature is directly proportional to average kinetic energy of particles.
Maxwell–Boltzmann distributions shows how kinetic energy is spread out amongst particles at a given temperature.

Full Notes

The Kinetic Molecular Theory (KMT) provides a particle-level model for understanding the macroscopic properties of gases—like pressure, volume, and temperature—based on particle motion and energy.

Core Assumptions of Kinetic Molecular Theory

Gas particles are in constant, random motion.
Gas particles occupy no volume (the volume of individual particles is negligible).
No intermolecular forces between particles (no attractions or repulsions).
Collisions between gas particles (and with container walls) are perfectly elastic.
The average kinetic energy of gas particles depends only on temperature (in kelvin).

Kinetic Energy and Temperature

Temperature isn’t just a number – it tells us about the average kinetic energy of the particles in a substance. When something feels hot, its particles are moving faster. When it feels cold, they’re moving slower.

Kinetic energy increases as temperature increases.

AP Chemistry diagram showing increased particle vibration and movement as temperature rises, illustrating that kinetic energy increases with temperature.

At absolute zero (0 K), particle motion stops completely — this is the theoretical lowest temperature possible.

The motion of gas particles is related to temperature by the equation:
KE = ½m v²

Where:
KE = kinetic energy (Joules)
m = mass of a particle (kg)
v = speed of the particle (m/s)

At a given temperature:

Lighter particles move faster
Heavier particles move slower, but both have the same average kinetic energy

Kelvin: The Scientific Temperature Scale

Kelvin (K) is the SI unit of temperature used in science.
It has the same step size as degrees Celsius (°C), but it starts from absolute zero instead of the freezing point of water.

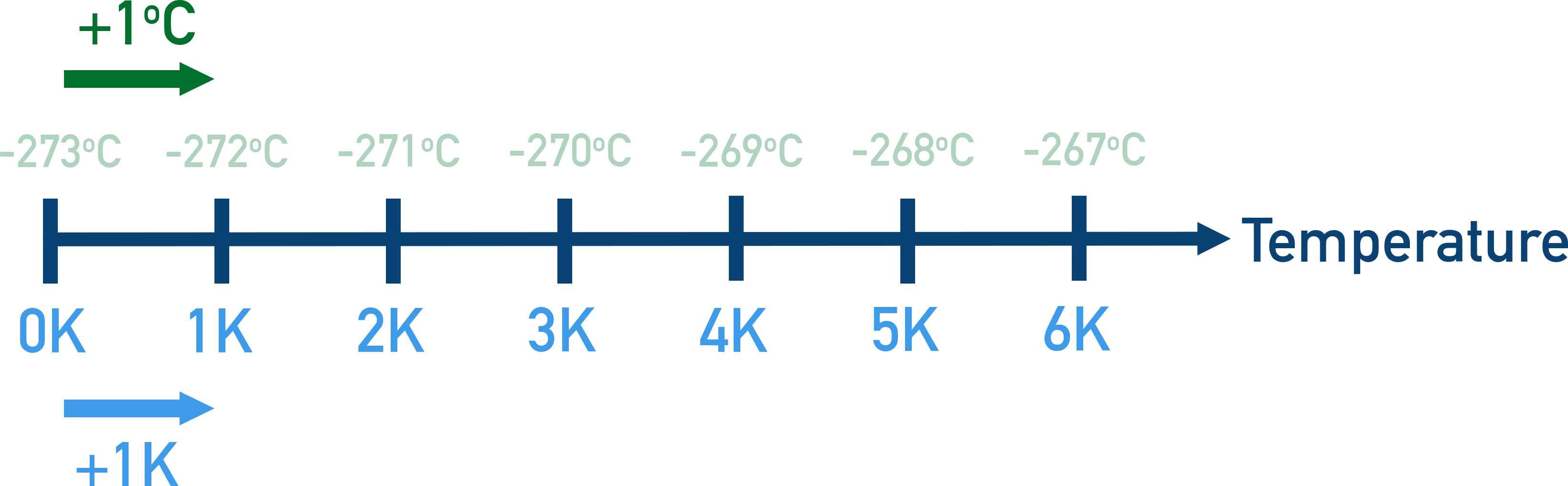
AP Chemistry temperature scale showing kelvin ticks from 0 K upward and matching steps to degrees Celsius to illustrate equal increments.

Converting between Celsius and Kelvin

To convert °C to K: K = °C + 273

To convert K to °C: °C = K − 273

Example25°C = 298 K; 100 K = −173°C

Temperature in kelvin is directly proportional to the average kinetic energy of particles.

Maxwell–Boltzmann Distribution

This is a graph that shows the distribution of kinetic energy (or particle speeds) in a gas sample at a given temperature.

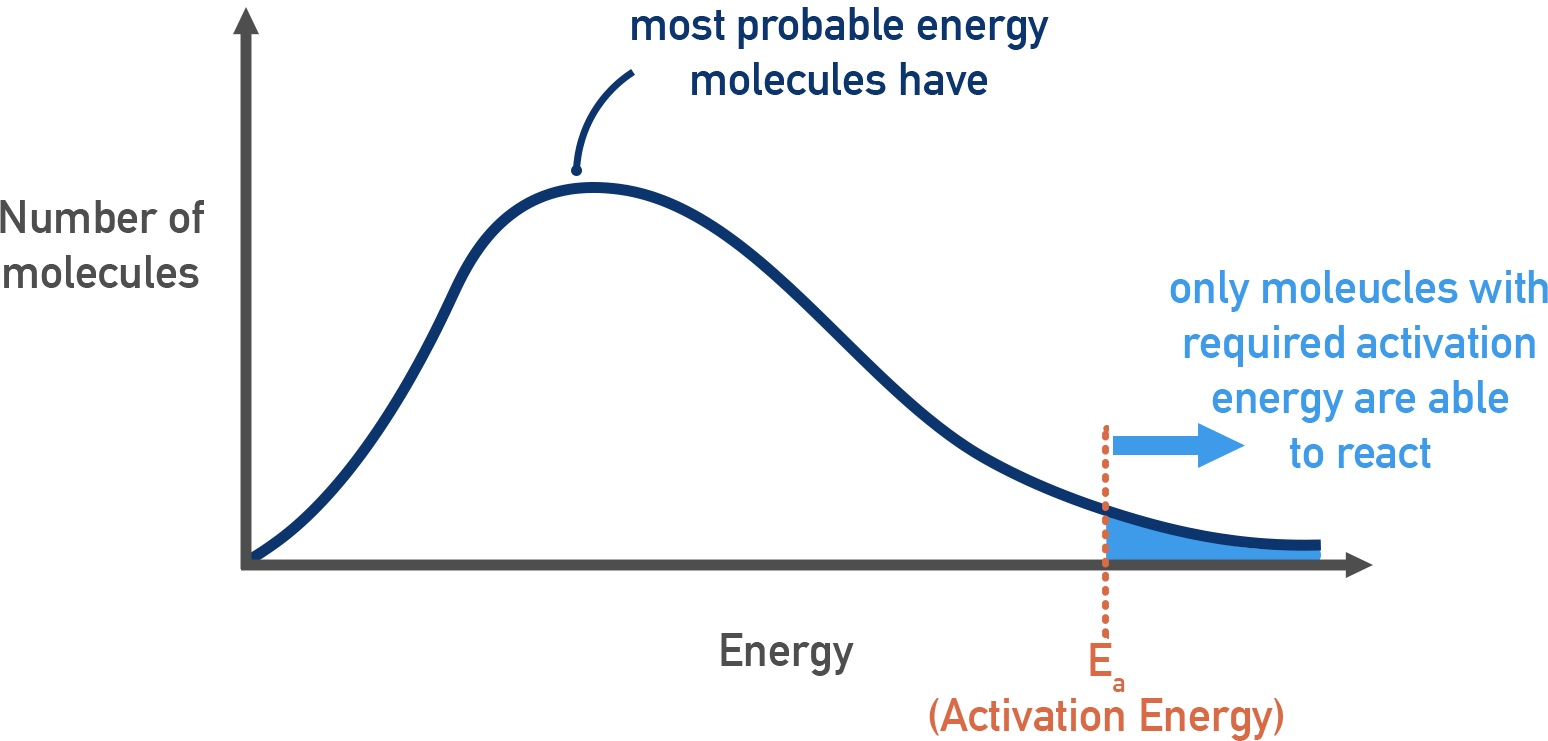
AP Chemistry Maxwell–Boltzmann curve showing number of molecules versus energy with activation energy threshold highlighted.

Key features

Most particles have speeds near the average value.
Some particles move much faster or much slower.
The curve is asymmetrical, with a long tail to the right.

As temperature increases

The peak of the curve flattens and shifts right.

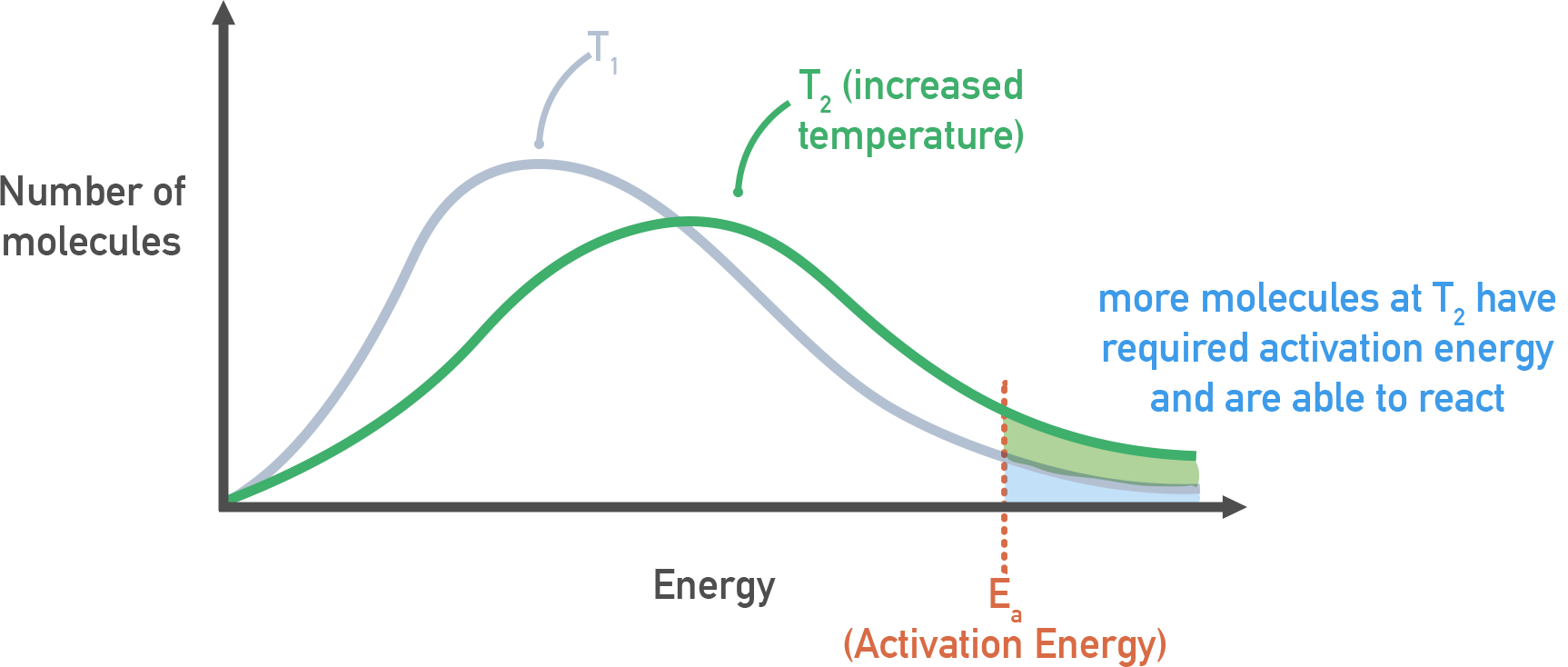
AP Chemistry overlayed Maxwell–Boltzmann curves at T₁ and higher T₂ showing shift to the right and lower peak; more molecules exceed activation energy Eₐ at higher temperature.

Particles move faster on average
The distribution becomes wider

This explains why increasing temperature causes an increase in pressure (particles collide more frequently and with more energy).

Particulate Model of Gas Behavior

At the particle level:

Gas pressure results from collisions between particles and the container walls.

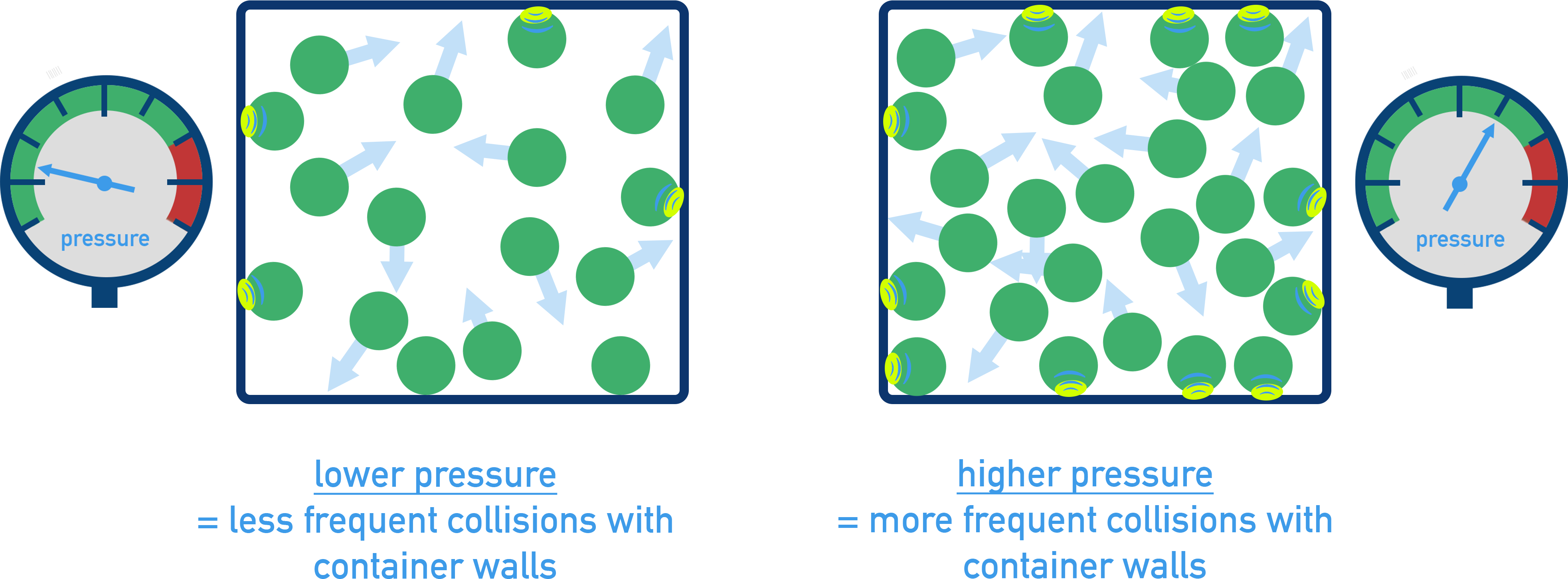
AP Chemistry particulate diagram comparing fewer versus more frequent gas particle collisions with container walls to illustrate lower and higher pressure.

More frequent or more energetic collisions = higher pressure.

Volume increases when particles have more energy (higher T) or fewer collisions (lower P)

This connects to:

Boyle’s law (P ∝ 1/V) — reducing volume increases collision frequency
Charles’s law (V ∝ T) — increasing temperature increases kinetic energy and volume

Gas Behaviour

Worked Example

At 300 K, which gas will have higher average speed: O₂ or He?

Both are at the same temperature, so both have the same average kinetic energy, but:
KE = ½m v² → v = √(2KE/m)
Helium has a smaller mass, so it must move faster to have the same kinetic energy.

Answer: Helium atoms move faster than oxygen molecules at the same temperature.

Matt’s exam tip

On questions involving kinetic energy and temperature, always convert to kelvin. For Maxwell–Boltzmann curves, remember: higher temp = lower peak and more spread out curve. Don’t confuse speed with kinetic energy — different gases at the same T have same KE but different speeds depending on mass.

Summary

The Kinetic Molecular Theory describes gases as particles in random motion, with pressure and temperature arising from their collisions and energy.
The Maxwell–Boltzmann distribution visually represents how particle speeds vary in a sample.
Importantly:
- KE = ½m v²
- Temperature (in K) ∝ average KE
- Lighter particles move faster than heavier ones at the same temperature
- Graphs shift right and flatten as temperature increases
Understanding these relationships helps link microscopic behavior with macroscopic gas laws like PV = nRT