AP | A-Level | IB | NCERT 11 + 12 – FREE NOTES, RESOURCES AND VIDEOS!
AP® Chemistry
YouTube Channel
YouTube Channel
@chemistry.student
1 Atomic Structure and Properties 2 Compound Structure and Properties 3 Properties of Substances and Mixtures 4 Chemical Reactions 5 Kinetics 6 Thermochemistry 7 Equilibrium 8 Acids and Bases 9 Thermodynamics and Electrochemistry

Equilibrium

7.1 Introduction to Equilibrium 7.2 Direction of Reversible Reactions 7.3 Reaction Quotient and Equilibrium Constant 7.4 Calculating the Equilibrium Constant 7.5 Magnitude of the Equilibrium Constant 7.6 Properties of the Equilibrium Constant 7.7 Calculating Equilibrium Concentrations 7.8 Representations of Equilibrium 7.9 Introduction to Le Châtelier’s Principle 7.10 Reaction Quotient and Le Châtelier’s Principle 7.11 Introduction to Solubility Equilibria 7.12 Common-Ion Effect

Common-Ion Effect

Learning Objective 7.12.A Identify the solubility of a salt, and/or the value of Ksp for the salt, based on the concentration of a common ion already present in solution.

Quick Notes

  • The common-ion effect refers to the decrease in solubility of an ionic compound when one of its ions is already present in the solution.
    • It is an application of Le Châtelier’s Principle: adding a product shifts equilibrium left, reducing dissociation.
  • The effect can be calculated using an ICE table and the Ksp expression.

Full Notes

What is the Common-Ion Effect?

When a salt is added to a solution that already contains one of its own ions, its solubility decreases. This is known as the common-ion effect.

Let’s take silver chloride (AgCl) as an example:

AgCl(s) ⇌ Ag+(aq) + Cl−(aq)

Normally, a small amount of AgCl dissolves until the system reaches equilibrium. But if the solution already contains Cl− ions, such as from added NaCl, this extra Cl− shifts the equilibrium to the left, according to Le Châtelier’s Principle (see Topic 7.9). As a result, less AgCl dissolves, and its solubility is reduced.

This effect can be observed when two saturated solutions—one of NaCl(aq) and one of AgCl(aq)—are mixed. The NaCl solution contributes a high concentration of Cl− ions. When these additional Cl− ions are introduced, they increase the product concentration in the equilibrium:

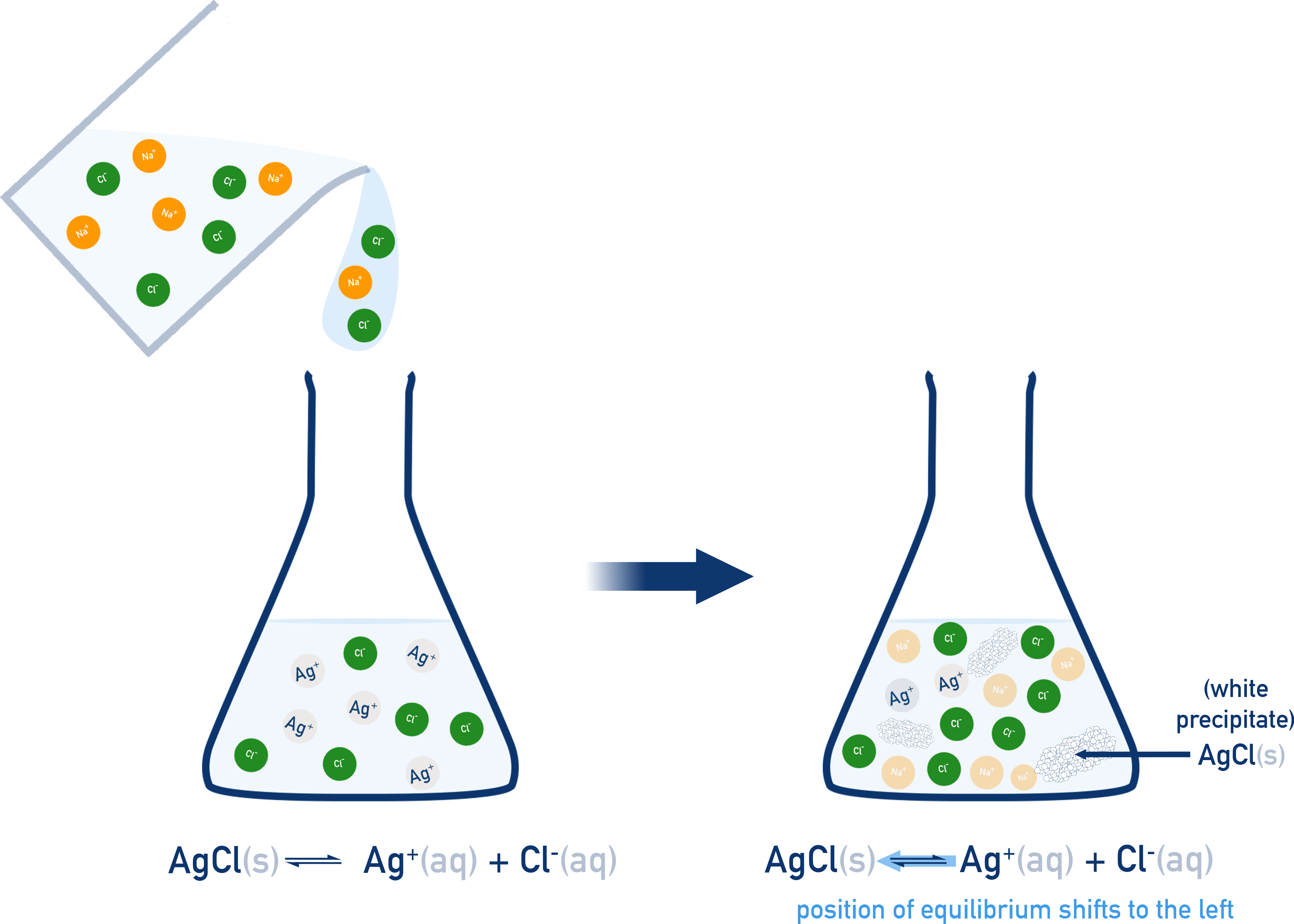
AP Chemistry diagram showing the common-ion effect: NaCl solution adds Cl− ions to AgCl equilibrium, shifting left to form precipitate AgCl(s).

According to Le Châtelier’s Principle, the system responds by shifting the equilibrium position to the left, reducing the concentration of ions in solution and forming more solid AgCl. As a result, a visible precipitate of AgCl forms.

This effect is important when predicting how soluble a salt will be in the presence of other dissolved substances. Even without full calculations, you can qualitatively explain the common-ion effect using equilibrium principles. Adding more of a product ion (like Cl− in the AgCl example) drives the system to form more solid and reduce the ion concentrations — ultimately lowering the salt’s solubility.

Explaining the Common-Ion Effect with Le Châtelier’s Principle

Example: Calculating Solubility with a Common Ion

Worked Example

What is the solubility of CaF2 in a solution of 0.10 M NaF?
Ksp of CaF2 = 3.9 × 10−11
Dissociation equation: CaF2(s) ⇌ Ca2+(aq) + 2F−(aq)

  1. Set up the ICE table
    Let the solubility of CaF2 be x mol/L.

    CaF2(s) Ca2+(aq) F−(aq)
    Initial – 0 0.10
    Change – +x +2x
    Equilibrium – x 0.10 + 2x
  2. Write the Ksp expression
    Ksp = [Ca2+][F−]2
    Substitute equilibrium values:
    Ksp = x(0.10 + 2x)2
  3. Simplify the expression
    Assume 2x ≪ 0.10, so:
    0.10 + 2x ≈ 0.10
    Ksp ≈ x(0.10)2 = 0.01x
  4. Solve for x
    3.9 × 10−11 = 0.01x
    x = 3.9 × 10−9 M
    This is the molar solubility of CaF2 in 0.10 M NaF solution.
  5. Compare to solubility in pure water
    In pure water (no added F−):
    CaF2(s) ⇌ Ca2+(aq) + 2F−(aq)
    [Ca2+] = x, [F−] = 2x
    Ksp = x(2x)2 = 4x3
    3.9 × 10−11 = 4x3
    x ≈ 2.1 × 10−4 M

Conclusion:

  • In pure water, the solubility of CaF2 is about 2.1 × 10−4 M.
  • In a solution with 0.10 M F− already present, the solubility drops to 3.9 × 10−9 M.
  • That’s a decrease by a factor of over 50,000, due to the common-ion effect.

Summary