AP | A-Level | IB | NCERT 11 + 12 – FREE NOTES, RESOURCES AND VIDEOS!
AP® Chemistry
YouTube Channel
YouTube Channel
@chemistry.student
1 Atomic Structure and Properties 2 Compound Structure and Properties 3 Properties of Substances and Mixtures 4 Chemical Reactions 5 Kinetics 6 Thermochemistry 7 Equilibrium 8 Acids and Bases 9 Thermodynamics and Electrochemistry

Equilibrium

7.1 Introduction to Equilibrium 7.2 Direction of Reversible Reactions 7.3 Reaction Quotient and Equilibrium Constant 7.4 Calculating the Equilibrium Constant 7.5 Magnitude of the Equilibrium Constant 7.6 Properties of the Equilibrium Constant 7.7 Calculating Equilibrium Concentrations 7.8 Representations of Equilibrium 7.9 Introduction to Le Châtelier’s Principle 7.10 Reaction Quotient and Le Châtelier’s Principle 7.11 Introduction to Solubility Equilibria 7.12 Common-Ion Effect

Calculating the Equilibrium Constant

Learning Objective 7.4.A Calculate Kc or Kp from experimental equilibrium concentrations or partial pressures.

Quick Notes

  • Kc uses equilibrium concentrations (mol dm−3) and Kp uses equilibrium partial pressures.
    • Both are calculated using equilibrium data (equilibrium concentrations for Kc or partial pressures for Kp).
  • Balanced chemical equations can be used to construct the correct equilibrium expression.
  • Only include species with variable concentration (don't include pure solids and liquids).
  • Units of K vary depending on the reaction and should be consistent with the expression.

Recap — What is the Equilibrium Constant?

The equilibrium constant measures the ratio of products to reactants at equilibrium for a given reaction.

AP Chemistry General reaction: aA + bB ⇌ cC + dD

The Kc expression (concentration):

Kc expression: Kc equals [C]^c [D]^d divided by [A]^a [B]^b

The Kp expression (partial pressure):

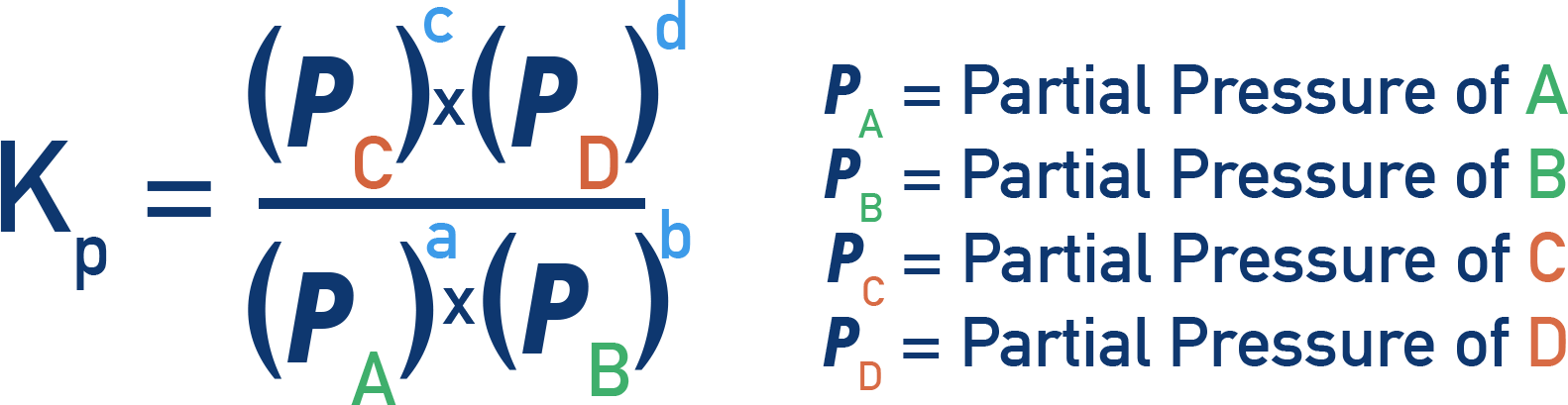
Kp expression written with partial pressures of gases raised to their stoichiometric powers

Steps to Calculate Kc or Kp

  1. Write the balanced equation. This gives you the molar ratios and sets the exponents (powers) for the K expression.
  2. Construct the K expression. Use concentrations for Kc, partial pressures for Kp.
  3. Insert equilibrium values. Read them from the question or determine them via an ICE table.
  4. Calculate. Apply exponents first; then multiply/divide to find K (and units if required).
Worked Example — Esterification (Kc)

Reaction: CH3COOH + C2H5OH ⇌ CH3COOC2H5 + H2O

Equilibrium concentrations: [CH3COOH] = 0.20, [C2H5OH] = 0.20, [CH3COOC2H5] = 0.40, [H2O] = 0.40 (mol dm−3)

  1. Kc = [ester][water] / ([acid][alcohol])
  2. Kc = (0.40 × 0.40) / (0.20 × 0.20) = 4.0

Since Kc > 1, equilibrium favours the products. This means in the equilibrium mixture there is a higher concentration of products (ester and water) compared to reactants.


Photo of Matt
Matt’s Exam Tip

Remember concentrations in the Kc expression are the concentrations of everything at equilibrium. Make sure you read questions carefully and, if needed, calculate equilibrium concentrations from given data (see below).


Worked Example — Kp from Total Pressure

Find Kp for the following system

Reaction: N2O4(g) ⇌ 2 NO2(g)

Given: total pressure = 400 kPa; n(N2O4) = 0.40, n(NO2) = 0.60.

  1. Mole fractions: χ(N2O4) = 0.40; χ(NO2) = 0.60.
  2. Partial pressures: P(N2O4) = 0.40×400 = 160 kPa; P(NO2) = 0.60×400 = 240 kPa.
  3. Kp = (P(NO2))2 / P(N2O4) = (240)2 / 160 = 360 kPa.

ICE Example

Finding an Unknown Equilibrium Concentration

Calculate the equilibrium concentration of H₂ for the following.

Reaction: H2(g) + I2(g) ⇌ 2HI(g),  K = 50.0 at 298 K

At equilibrium: [HI] = 0.80 mol dm−3, [I2] = 0.10 mol dm−3. Find [H2].

Species Initial Change Equilibrium
H2a−0.40a − 0.40
I2—−0.400.10
HI0+0.800.80
  1. K = [HI]2 / ([H2][I2])
  2. 50.0 = (0.80)2 / [(a − 0.40)(0.10)] → 0.10(a − 0.40) = 0.0128
  3. a − 0.40 = 0.128 → a = 0.528 → [H2] = a − 0.40 = 0.128 mol dm−3.

Approximation Use (K ≪ 1)

If K is very small, then very little product is present at equilibrium. Because of this, we can assume the reactant’s equilibrium concentration is approximately its initial value.

Worked Example

For Example:
Lets take the following equilibrium,
A ⇌ B
The equilibrium constant is K = 1.0 × 10⁻⁵
Initially:
[A] = 0.20 mol dm⁻³
[B] = 0 mol dm⁻³
Estimate the equilibrium concentration of B.

  1. Step 1: ICE table (assume small change)
    Let the change in A be –x and the change in B be +x:
    Species Initial Change Equilibrium
    A 0.20 –x 0.20 – x
    B 0 +x x
  2. Step 2: Write expression for K
    K = [B] / [A] = x / (0.20 – x)
    Since K is very small, we assume that x is small and so 0.20 – x ≈ 0.20
    So:
    1.0 × 10⁻⁵ = x / 0.20
    x = 0.20 × 1.0 × 10⁻⁵ = 2.0 × 10⁻⁶ mol dm⁻³

Conclusion:
At equilibrium, only a tiny amount of B is formed, and [A] hardly changes – justifying the approximation.
So:
[A] ≈ 0.20 mol dm⁻³
[B] ≈ 2.0 × 10⁻⁶ mol dm⁻³

Summary