pH, pOH, and K_w

Full Notes

H₃O⁺ and OH⁻: Understanding Water’s Equilibrium

In any aqueous solution, water molecules are constantly undergoing a process called autoionization, where two water molecules react to form hydronium (H₃O⁺) and hydroxide (OH⁻) ions:

H₂O + H₂O ⇌ H₃O⁺ + OH⁻

This equilibrium lies far to the left—meaning only a tiny amount of water actually ionizes. But even pure water contains equal and very small concentrations of H₃O⁺ and OH⁻ ions.

• If [H₃O⁺] > [OH⁻], the solution is acidic.
• If [OH⁻] > [H₃O⁺], the solution is basic (alkaline).

To describe and calculate these concentrations more conveniently, we use pH and pOH – logarithmic scales that make sense of very small numbers.

A Note on H⁺ and H₃O⁺

You’ll often see H⁺(aq) used to represent the hydrogen ion in solution. Technically though, free protons (H⁺) don’t float around in water – they quickly bond with water molecules to form H₃O⁺(aq) (hydronium ions).

For AP Chemistry, it’s best to use H₃O⁺ to accurately reflect what’s happening in aqueous solutions however don't be surprised when you see H⁺ used (including on this site).

Key Definitions

• [H₃O⁺] or [H⁺]: Concentration of hydronium ions (mol/L)
• [OH⁻]: Concentration of hydroxide ions (mol/L)
• K_w: The ion-product constant for water

K_w = [H₃O⁺][OH⁻] = 1.0 × 10⁻¹⁴ (at 25 °C)

pH:

pOH:

pK_w:

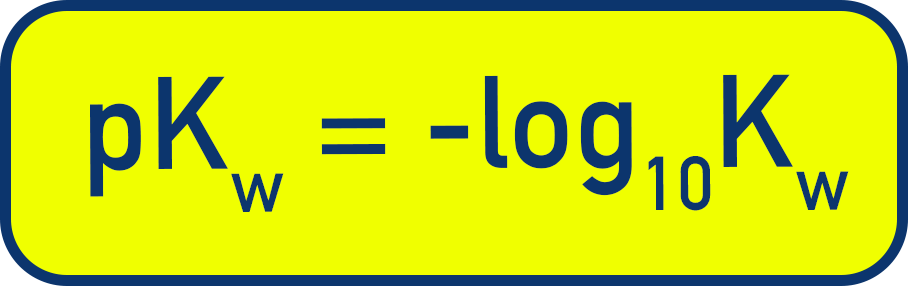
= 14.00 at 25 °C
So: pH + pOH = 14.00

Neutral Water at 25 °C

In pure water, the concentrations of H₃O⁺ and OH⁻ are equal:

[H₃O⁺] = [OH⁻] = 1.0 × 10⁻⁷ mol/L

pH = −log(1.0 × 10⁻⁷) = 7.00
pOH = 7.00

So, water is neutral when pH = 7.00 — but only at 25 °C. Since K_w changes with temperature, the “neutral” pH shifts slightly depending on conditions.

Matt’s exam tip

Don’t get confused. Neutral means [H₃O⁺] and [OH⁻] are the same. Pure water will always be neutral, however its pH value will change depending on temperature because the actual concentrations of [H₃O⁺] and [OH⁻] are temperature dependent.

Why Use pH and pOH?

The concentrations of H₃O⁺ and OH⁻ can be very small or very large. Logarithmic scales make these values more manageable and easier to work with.

• High [H₃O⁺] means a low pH and acidic solution.
• Low [H₃O⁺] means a high pH and basic solution.

The pH scale is logarithmic, which means that each pH change of 1 corresponds to a tenfold change in the hydronium ion concentration:

• A solution with a pH of 3 has 10× more H₃O⁺ than a solution with a pH of 4.
• A solution with a pH of 5 is 100× more acidic than a solution with a pH of 7.

pH and pOH give us a clearer sense of how acidic or basic a solution is without needing to handle extremely small numbers.

Converting Between pH and Concentrations

To find [H₃O⁺] from pH:

To find [OH⁻] from pOH:

You can also move between pH and pOH using:
pH + pOH = 14.00

Worked Example