AP | A-Level | IB | NCERT 11 + 12 – FREE NOTES, RESOURCES AND VIDEOS!
OCR (A) A-Level
YouTube Channel
YouTube Channel
@chemistry.student
*Revision Materials and Past Papers* 2.1.1 Atomic structure and isotopes 2.1.2 Compounds, formulae and equations 2.1.3 Amount of substance 2.1.4 Acids 2.1.5 Redox 2.2.1 Electron structure 2.2.2 Bonding and structure 3.1.1 Periodicity 3.1.2 Group 2 3.1.3 The halogens 3.1.4 Qualitative analysis 3.2.1 Enthalpy 3.2.2 Reaction Rates 3.2.3 Chemical equilibrium 4.1 Basic concepts and hydrocarbons 4.1.2 Alkanes 4.1.3 Alkenes 4.2.1 Alcohols 4.2.2 Haloalkanes 4.2.3 Organic synthesis 4.2.4 Analytical techniques 5.1.1 How fast? 5.1.2 How far? 5.1.3 Acids, bases and buffers 5.2.1 Lattice enthalpy 5.2.2 Enthalpy and entropy 5.2.3 Redox and electrode potentials 5.3.1 Transition elements 5.3.2 Qualitative analysis 6.1.1 Aromatic compounds 6.1.2 Carbonyl compounds 6.1.3 Carboxylic acids and esters 6.2.1 Amines 6.2.2 Amino acids, amides and chirality 6.2.3 Polyesters and polyamides 6.2.4 Carbon–carbon bond formation 6.2.5 Organic synthesis 6.3.1 Chromatography and qualitative analysis 6.3.2 Spectroscopy Required Practicals

5.1.2 How far?

Equilibrium

Equilibrium (Kc and Kp)

Specification Reference 5.1.2 (a)–(h)

Quick Notes

  • Mole fraction (χ) = moles of gas A ÷ total moles of gas
  • Partial pressure = mole fraction × total pressure
  • Quantities at Equilibrium:
    • Use ICE (Initial, Change, Equilibrium) tables to calculate concentrations or pressures at equilibrium from starting amounts and stoichiometry
  • Techniques for determining equilibrium quantities: titration, colorimetry, pH measurement, gas volume collection depending on the system
  • Expressions for Kc and Kp
    • Kc:
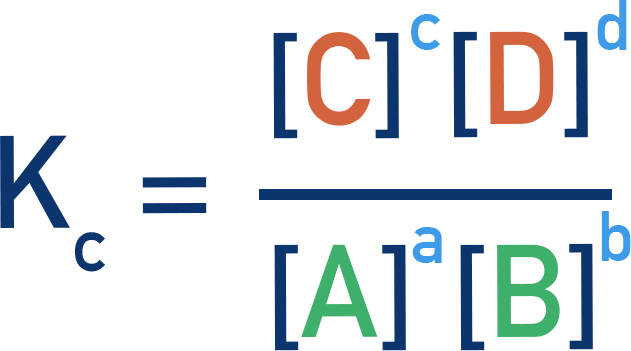      OCR (A) A-Level Chemistry general Kc expression with products over reactants. concentrations in mol dm−3
    • Kp: 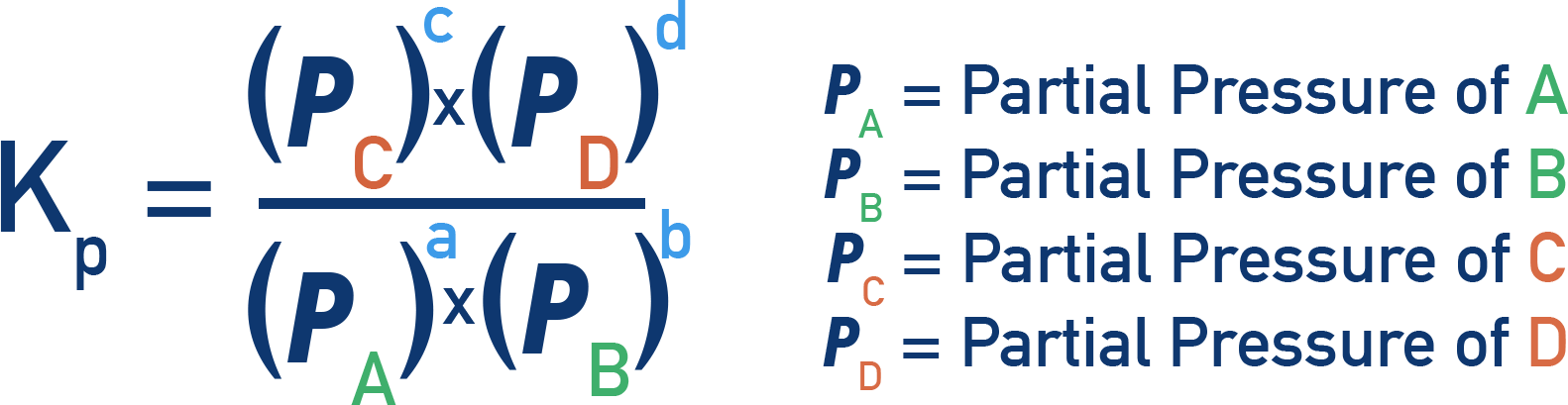OCR (A) A-Level Chemistry Kp expression with partial pressures of products over reactants. partial pressures of gases
    • Only include gases and aqueous species in the expressions
  • Temperature effects:
    • Increasing temperature favours endothermic direction and Kc and Kp change accordingly
  • Catalyst, concentration, pressure changes: no effect on Kc or Kp
  • Position of Equilibrium:
    • If K increases = favours products
    • If K decreases = favours reactants
  • Applies also to Ka, Kw and other equilibrium constants

Full Notes

Equilibrium Constant, Kc

Kc is an equilibrium constant and shows the position of equilibrium for reactions in homogeneous equilibrium.

A homogenous equilibrium means all reactants and products are in the same phase.

Kc is calculated using the concentrations of reactants and products in the mixture at equilibrium.

General Formula for Kc

For a reaction:

OCR (A) A-Level Chemistry general reaction aA + bB ⇌ cC + dD used for equilibrium constant expression.

Kc =

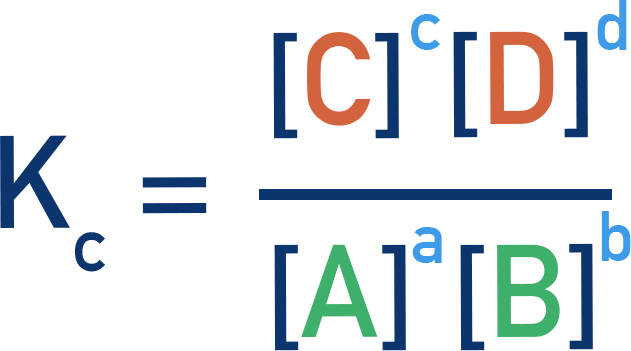
OCR (A) A-Level Chemistry equilibrium constant Kc expression showing concentrations of C and D over A and B.

where [A], [B], [C], [D] are equilibrium concentrations in mol dm−3 and a, b, c, and d are the balancing numbers from the equation.

If...

Kc values are only valid for a specific temperature - Kc changes with temperature.

Photo of Matt
Matt’s exam tip

Solids aren’t ever included in Kc expressions and if water is a solvent, it also isn’t included (even if it is also a reactant or product).

How to Calculate Kc

Worked Example: Esterification Reaction

CH3COOH + C2H5OH ⇌ CH3COOC2H5 + H2O

Equilibrium concentrations:
[CH3COOH] = 0.20 mol dm⁻³
[C2H5OH] = 0.20 mol dm⁻³
[CH3COOC2H5] = 0.40 mol dm⁻³
[H2O] = 0.40 mol dm⁻³

  1. Kc = [CH3COOC2H5][H2O] ÷ [CH3COOH][C2H5OH]
  2. = (0.40 × 0.40) ÷ (0.20 × 0.20)
  3. = 4.0

Since Kc > 1, equilibrium favours the products. This means in the equilibrium mixture there is a higher concentration of products (ester and water) compared to reactants.


Photo of Matt
Matt’s exam tip

Remember concentrations in Kc are equilibrium values. Always check if you need to calculate equilibrium concentrations from given data first.

Effect of Changing Conditions on Kc

Kp (Equilibrium Constant for Gases)

Kp has been outlined in more detail here.
This page is just what you need to know for OCR (A) A-level :)

The equilibrium constant, Kp, works in the same way as Kc (see above).

For the General reaction:

OCR (A) A-Level Chemistry general gaseous equilibrium aA(g) + bB(g) reversible reaction to cC(g) + dD(g).

The Kp expression is:

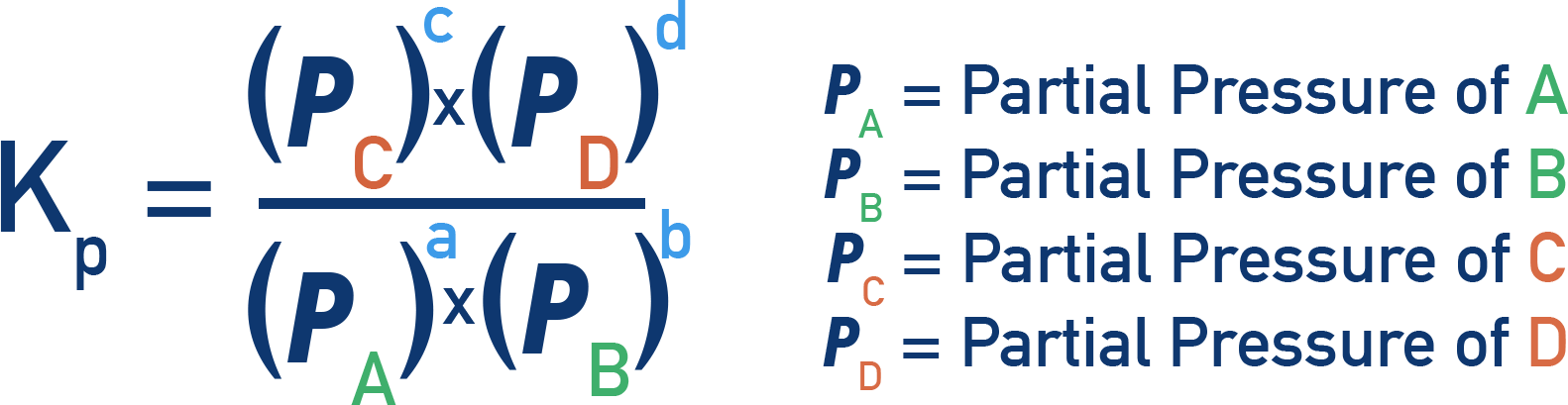
OCR (A) A-Level Chemistry Kp expression showing product partial pressures over reactant partial pressures with powers as stoichiometric coefficients.

Calculating Partial Pressure

The total pressure of a gaseous system at equilibrium is directly related to the number of moles of each gas in the mixture. How much pressure one type of gas contributes to the total pressure of a gaseous system is called its partial pressure. All partial pressures of gases in a system add up to give the total pressure of the system.

It is calculated using:

AQA A-Level Chemistry formula: partial pressure of a gas equals mole fraction of the gas times total pressure.

The mole fraction of a gas is the moles of that gas in the mixture compared to moles of all gases. It is calculated using:

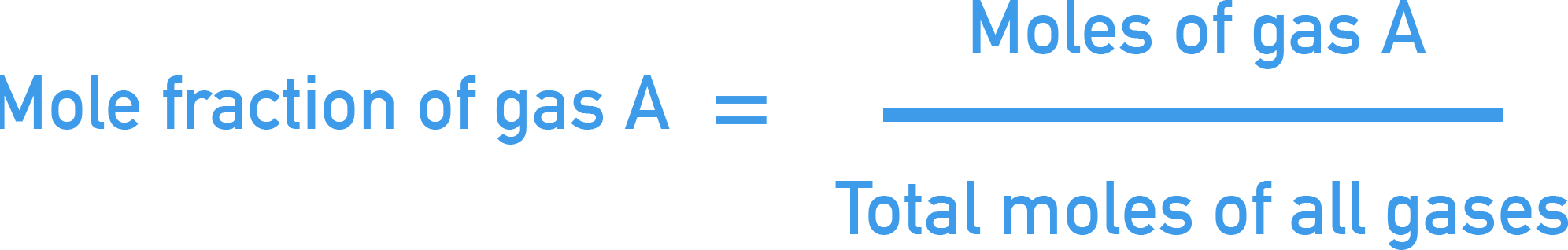
AQA A-Level Chemistry formula: mole fraction of gas A equals moles of gas A divided by total moles of all gases.

Worked Example

Worked Example

Find Kp for the following system, given the total pressure = 400 kPa and the moles of N₂O₄ and NO₂ at equilibrium are 0.40 and 0.60, respectively.

N₂O₄ (g) ⇌ 2NO₂ (g)

Given:
Total pressure = 400 kPa
Moles of N₂O₄ = 0.40
Moles of NO₂ = 0.60

  1. Calculate mole fractions
    X(N₂O₄) = 0.40 / (0.40 + 0.60) = 0.40
    X(NO₂) = 0.60 / (0.40 + 0.60) = 0.60
  2. Calculate partial pressures
    P(N₂O₄) = 0.40 × 400 = 160 kPa
    P(NO₂) = 0.60 × 400 = 240 kPa
  3. Write Kp expression
    Kp = (P²[NO₂]) / P[N₂O₄]
  4. Substitute
    Kp = (240²) / (160) = 360 kPa

Answer: Kp = 360 kPa.

Effect of Temperature on Kp

Kp only changes with temperature and we can predict the effect of changing temperature on Kp values.

Effect of Pressure and Concentration on Kp

Kp remains constant when pressure or concentration are changed.
The system shifts equilibrium to restore Kp.

For Example: N₂O₄ ⇌ 2NO₂
If the total pressure is increased:

Effect of a Catalyst on Kp

A catalyst does not affect Kp because it does not change equilibrium position.
A catalyst lowers activation energy, so equilibrium is reached faster, but the position of equilibrium remains unchanged.

ICE Tables and Equilibrium Calculations

To calculate equilibrium quantities, we can use initial quantities and stoichiometry of the balanced equation with an ICE table.

ICE table:

Worked Example: Equilibrium Concentrations

For the equilibrium:
N2(g) + 3H2(g) ⇌ 2NH3(g)
At a certain temperature, 1.00 mol of N2 and 3.00 mol of H2 are placed in a 1.00 dm³ container. At equilibrium, there are 0.80 mol of NH3 present.
Calculate the equilibrium concentrations of N2 and H2.

Step 1: Set up the ICE table

Species N2 H2 NH3
Initial (mol) 1.00 3.00 0.00
Change (mol) −x −3x +2x
Equilibrium 1.00 − x 3.00 − 3x 2x = 0.80

Step 2: Use known value
From 2x = 0.80, solve for x: x = 0.40

Step 3: Calculate equilibrium moles
N2: 1.00 – 0.40 = 0.60 mol
H2: 3.00 – 3(0.40) = 1.80 mol
NH3: already given = 0.80 mol

Step 4: Convert to concentrations (in mol/dm³)
Since the volume is 1.00 dm³, concentrations = moles:
[N2] = 0.60 mol/dm³
[H2] = 1.80 mol/dm³
[NH3] = 0.80 mol/dm³

Experimental Determination of Equilibrium Quantities

Determining quantities of substances at equilibrium can be challenging and the method used depends on the system. Examples include:

Summary