AP | A-Level | IB | NCERT 11 + 12 – FREE NOTES, RESOURCES AND VIDEOS!
OCR (A) A-Level
YouTube Channel
YouTube Channel
@chemistry.student
*Revision Materials and Past Papers* 2.1.1 Atomic structure and isotopes 2.1.2 Compounds, formulae and equations 2.1.3 Amount of substance 2.1.4 Acids 2.1.5 Redox 2.2.1 Electron structure 2.2.2 Bonding and structure 3.1.1 Periodicity 3.1.2 Group 2 3.1.3 The halogens 3.1.4 Qualitative analysis 3.2.1 Enthalpy 3.2.2 Reaction Rates 3.2.3 Chemical equilibrium 4.1 Basic concepts and hydrocarbons 4.1.2 Alkanes 4.1.3 Alkenes 4.2.1 Alcohols 4.2.2 Haloalkanes 4.2.3 Organic synthesis 4.2.4 Analytical techniques 5.1.1 How fast? 5.1.2 How far? 5.1.3 Acids, bases and buffers 5.2.1 Lattice enthalpy 5.2.2 Enthalpy and entropy 5.2.3 Redox and electrode potentials 5.3.1 Transition elements 5.3.2 Qualitative analysis 6.1.1 Aromatic compounds 6.1.2 Carbonyl compounds 6.1.3 Carboxylic acids and esters 6.2.1 Amines 6.2.2 Amino acids, amides and chirality 6.2.3 Polyesters and polyamides 6.2.4 Carbon–carbon bond formation 6.2.5 Organic synthesis 6.3.1 Chromatography and qualitative analysis 6.3.2 Spectroscopy Required Practicals

2.1.3 Amount of substance

Determination of formulaePercentage yields and atom economyThe Mole and Calculation of reacting masses, gas volumes and mole concentrations

Amount of Substance, The Mole and Calculation of Reacting Masses, Gas Volumes

Specification Reference 2.1.3 (a), (e), (f), (g)

Quick Notes

  • Mole (mol): Unit for amount of substance
  • Avogadro constant (Na) = 6.02 × 1023 particles mol−1
  • Molar mass = mass per mole (g mol−1)
  • Molar gas volume at RTP = 24.0 dm3 mol−1
  • Calculations Involving Moles
    • Mass: moles = mass ÷ molar mass
    • Gases: moles = volume ÷ 24.0 (at RTP)
    • Solutions: moles = concentration × volume (in dm3)
  • Ideal Gas Equation
    • pV = nRT
    • p in Pa, V in m3, T in K, R = 8.31 J mol−1 K−1
  • Percentage Yield and Atom Economy
    • Percentage yield = (actual ÷ theoretical) × 100
    • Atom economy = (mass of desired product ÷ total mass of products) × 100

Full Notes

The Mole and Amount of Substance

The mole (mol) is a standard unit for measuring amounts in chemistry.

One mole of any substance contains 6.02 × 1023 particles, which is known as the Avogadro constant (Na).

Molar mass is the mass of one mole of a substance, expressed in g mol−1.

At room temperature and pressure (RTP), one mole of any gas occupies a volume of 24.0 dm3. This is molar gas volume.

Calculations Using the Mole

There are several ways we can calculate moles, depending on the measured data provided.

Moles from Mass

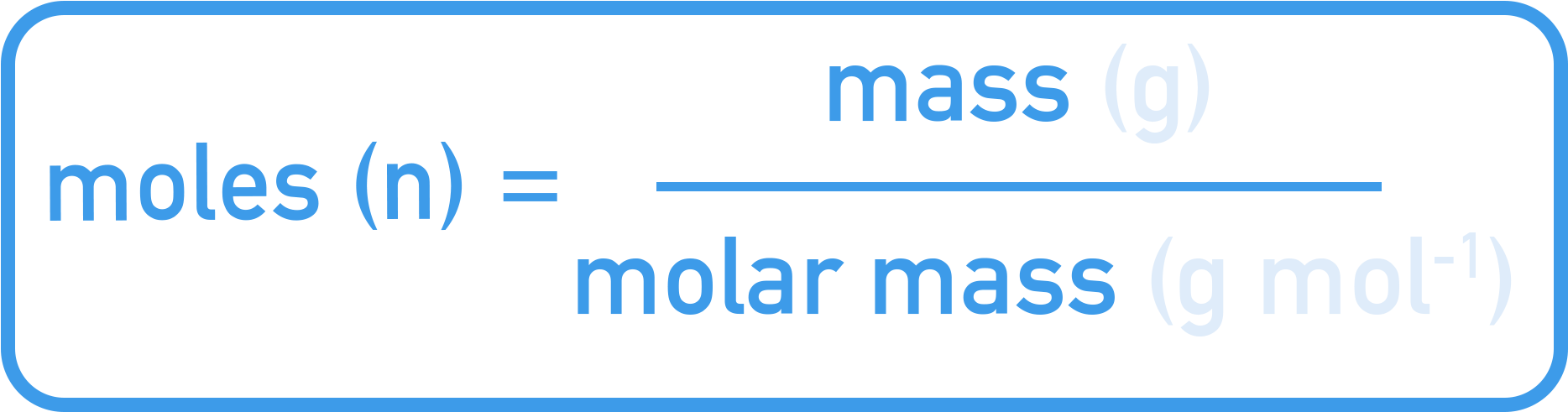
OCR (A) A-Level Chemistry formula diagram for calculating moles from mass and molar mass.
Worked Example: Moles from Mass

How many moles in 18 g of water (H2O)?

  1. Mr of H2O = 2(1) + 16.0 = 18.0
  2. Moles = mass ÷ Mr = 18 ÷ 18.0 = 1 mol

Worked Example: Mass from Moles

What is the mass of 2 moles of methane (CH4)?

  1. Mr of CH4 = 4(1.0) + 12.0 = 16.0
  2. Mass = Moles × Mr = 2 × 16.0 = 32 g

Using the Avogadro Constant

We can use the Avogadro constant to work between moles and number of particles of something.

OCR (A) A-Level Chemistry formula diagram showing relationship between number of particles, moles, and Avogadro constant.
Worked Example

How many molecules in 0.5 mol of O2?

  1. Number of molecules = 0.5 × Na
  2. = 0.5 × (6.02 × 1023) = 3.01 × 1023

Photo of Matt
Matt’s Exam Tip

When working with the Avogadro constant, don’t be surprised if answers seem very big (when finding numbers of particles) or very small (finding masses of individual particles). Remember the Avogadro constant is enormous!

Concentration of Solutions

When dealing with solutions, concentration is the amount of a substance (in moles) per 1 dm3 of solution. Common units: mol dm−3.

Moles from Concentration and Volume

OCR (A) A-Level Chemistry formula diagram showing calculation of moles from concentration and volume.
Worked Example

What is the concentration of a solution made by dissolving 0.1 mol of NaOH in 250 cm3 of solution?

  1. Volume = 250 ÷ 1000 = 0.250 dm3
  2. Concentration = 0.1 ÷ 0.250 = 0.4 mol dm−3

Photo of Matt
Matt’s Exam Tip

Make sure volume is always in dm3 when using these formulas (divide cm3 by 1000 to do this).

Understanding the Ideal Gas Equation

Note: ideal gases and the ideal gas equation are covered in more detail here.

The ideal gas equation is:

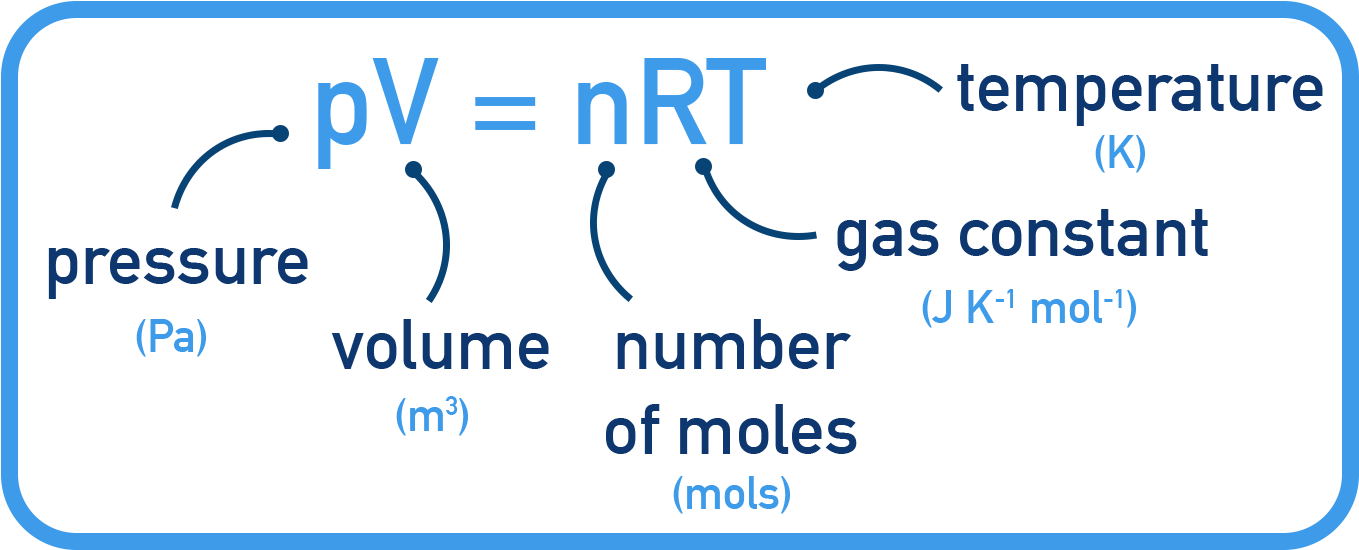
OCR (A) A-Level Chemistry formula diagram for the ideal gas equation PV = nRT.

This equation relates pressure (P), volume (V), temperature (T), and moles (n) of a gas.

The gas constant (R) has a value of 8.314 J mol−1 K−1.

Units Breakdown

Quantity Unit
Pressure Pa
Volume m3
Temperature K
Moles mol
Gas constant (R) 8.314 J mol−1 K−1

Unit Conversions for the Ideal Gas Equation

Using the Ideal Gas Equation

Worked Example: Finding Volume

A gas sample has P = 100 kPa, n = 0.50 mol, and T = 298 K. What is its volume?

  1. Convert pressure to Pa: 100 kPa = 100,000 Pa
  2. Rearrange the ideal gas equation for volume: V = (nRT) ÷ P
  3. Plug in the values: V = (0.50 × 8.314 × 298) ÷ 100000
  4. Solve: V = 1238.3 ÷ 100000 = 0.0124 m3 = 12.4 dm3

Photo of Matt
Matt’s Exam Tip

Be really careful with units when using the ideal gas equation, especially converting temperatures to Kelvin (K) and volumes to m3.

Summary