Free A-level and IB Chemistry Notes, Resources and Tutorials 

AS-Level Amounts of Substance

Video Tutorial Moles - Gases

Quick Notes Moles - Gases

  • The ideal gas equation is used to calculate the moles of gas present in a system if the volume, pressure and temperature are known.
    • pV = nRT
      • n = moles
      • R = gas constant = 8.31 Jmol-1K-1
      • V = volume (m3)
      • p = pressure (Pa)
      • T = temperature (K)
  • The equation assumes that all gases behave in the same way and are not interacting with each other, they are described as ‘ideal gases’.
  • At room temperature and pressure (293K and 101kPa), the ideal gas equation shows that 1 mole of any gas occupies a total volume of 24000cm3 (24dm3).
  • At standard temperature and pressure (273K and 101kPa), the ideal gas equation shows that 1 mole of any gas occupies a total volume of 22400cm3 (22.4dm3).

Full Notes Moles - Gas

When finding the number of moles of a gas, we use the same principle as with liquids and solids, but there are other considerations we need to take into account.

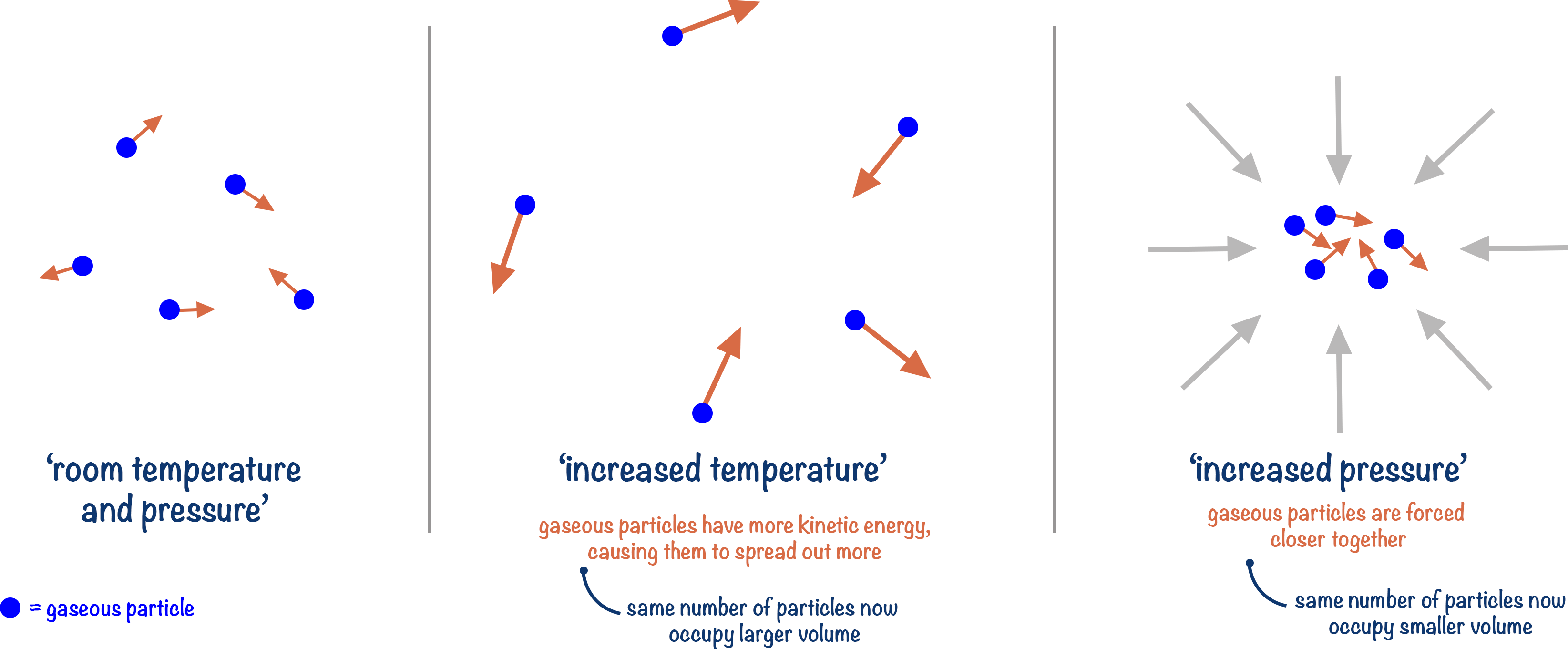
Pressure and temperature influence the number of moles of gas found in a given volume.

One mole of gaseous molecules will occupy a larger volume at higher temperatures compared to lower temperatures. Equally, one mole of gaseous molecules will occupy a smaller volume at higher pressures compared to lower pressures.

This means pressure, temperature and volume are all linked when it comes to finding the moles of gas in a container or system.

 

how pressure changes volume occupied by gas particles a-level chemistry

 

At room temperature and pressure, we assume that 1 mole of ANY gas occupies 24 000cm3 of space. From this we can easily calculate how many moles of that gas we may have.

 

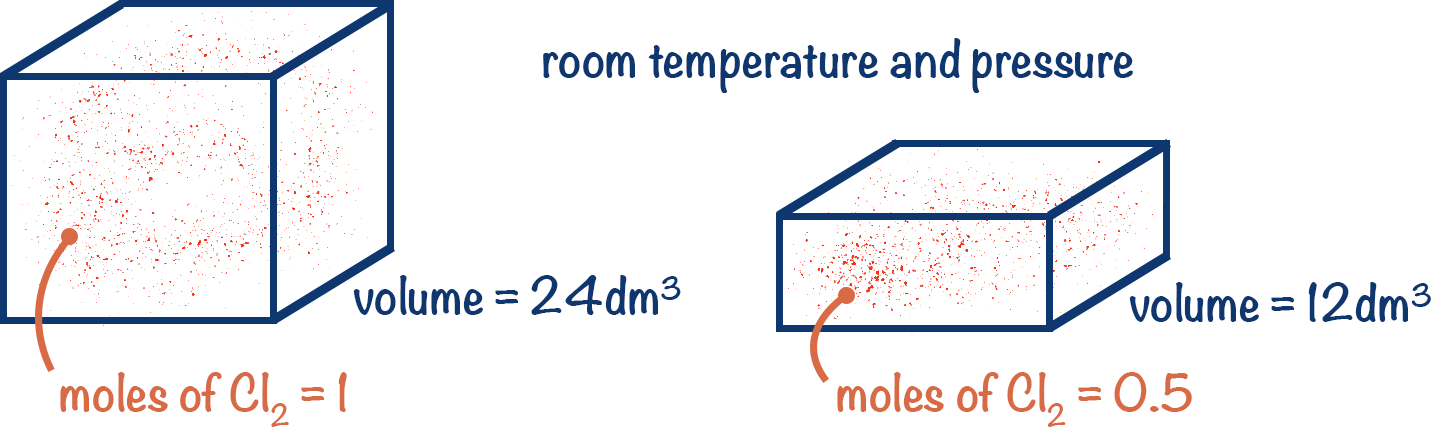
volume occupied by one mole of a gas at room temperature and pressure

 

For example, if a sample of Cl2 gas has a volume of 24 000cm3 at room temperature and pressure, there is 1 mole of Cl2 molecules in the sample. Therefore, if a sample of Cl2 gas has a volume of 12 000cm3 at room temperature and pressure, there are 0.5 moles of Cl2 molecules present.

Ideal Gas Equation

What happens if the gas is not at room temperature or pressure though?

We link pressure, volume, temperature and moles of gas using the ideal gas equation: pV = nRT.

 

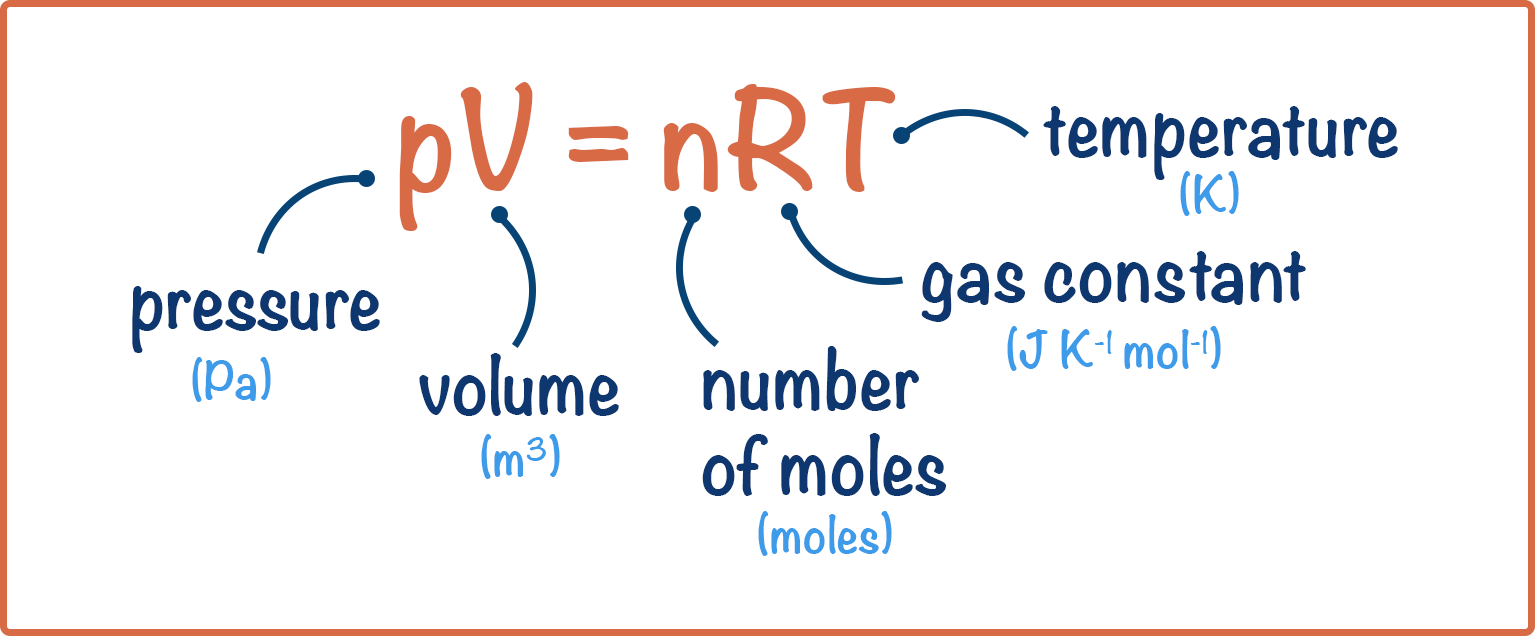
ideal gas equation with units a-level chemsitry

 

where: p = pressure (Pa), V = volume (m3), n = number of moles, R = gas constant and T = temperature (in Kelvin)

A few things to point out:

Pressure is in pascals (Pa not kPa) – a particular favourite for examiners is to give you the pressure in a question as kPa, but you must convert to Pa for the ideal gas equation (multiply by 1000 as 1kPa = 1000Pa).

Volume is in m3 not dm3 (divide dm3 by 1000 to get m3).

Temperature is in Kelvin. To convert from degrees Celsius to Kelvin, add 273.

We call this equation the ideal gas equation, as it assumes all the gases in the system are behaving as ideal gases.