Bohr’s Model for Hydrogen Atom
Learning Objective: Understand how Bohr’s quantized circular orbits explain hydrogen’s spectrum, how to use radius and energy expressions, and why the model has limitations.
Quick Notes:
- Bohr explained hydrogen's atomic structure using quantized circular orbits.
- Electrons can only occupy discrete energy levels without radiating energy.
- Energy is emitted or absorbed only when the electron jumps between levels.
- Bohr’s model explains line spectrum of hydrogen well, but fails for atoms with more than one electron and can't account for fine spectra or quantum mechanics.
Full Notes:
Background to Bohr’s Model
Classical mechanics, as used in Rutherford’s model, could not explain the stability of atoms or the line spectra of hydrogen.
Bohr introduced a new atomic model in 1913, combining classical ideas with quantum postulates to overcome these issues.
Postulates of Bohr’s Atomic Model
1. Stable Circular Orbits (Stationary States)
Electrons revolve around the nucleus in circular orbits with fixed radii and energy, called stationary states, without emitting radiation as they move.
2. Quantization of Angular Momentum
Only orbits are permitted where the electron’s angular momentum is an integral multiple of h/2π.
Formula:

mₑ × v × r = n × h / (2π) (Equation 2.11)
- m = mass of the electron
- v = velocity of the electron
- r = radius of the orbit
- h = Planck’s constant = 6.626 × 10−34 J·s
- n = principal quantum number (n = 1, 2, 3, …)
3. Emission or Absorption of Radiation
Electrons can jump between energy levels by emitting or absorbing a photon of radiation.
The energy gaps can be described by the Bohr’s Frequency Rule formula:

ν = ΔE / h = (E₂ – E₁) / h (Equation 2.10)
- E₂ = energy of higher orbit
- E₁ = energy of lower orbit
- ν = frequency of radiation emitted or absorbed
Energy and Radius of Bohr Orbits for Hydrogen
Note - you don’t need to know the derivations or advanced theory behind these equations, just how they can be used and what they describe
For hydrogen atom (Z = 1), Bohr showed:
Radius of nth orbit:
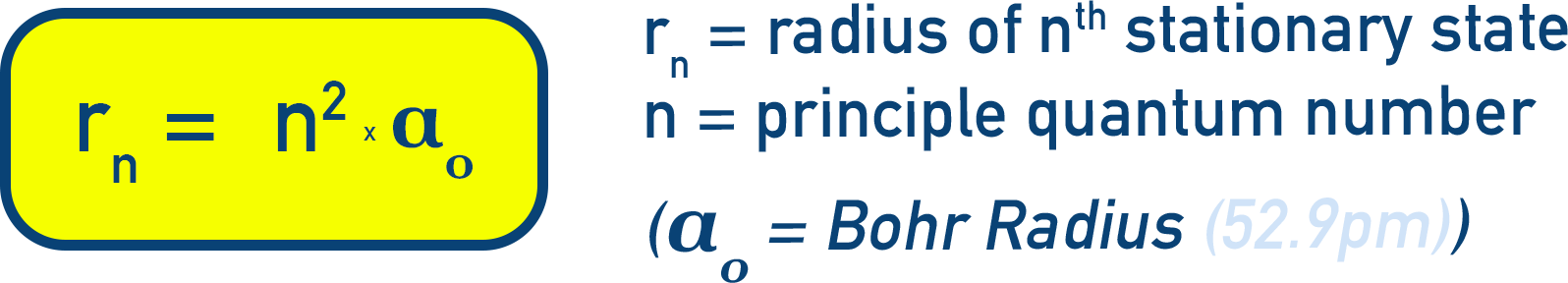
rn = n² × a₀ (Equation 2.12)
(Where 1 Å = 10−10 m)
This means the radius of the first stationary state (n=1) is 52.9pm. This is called the Bohr Radius or Bohr Orbit.
And, as n increases, the distance of the orbit the electron is in is further from the nucleus.
Energy of nth orbit:
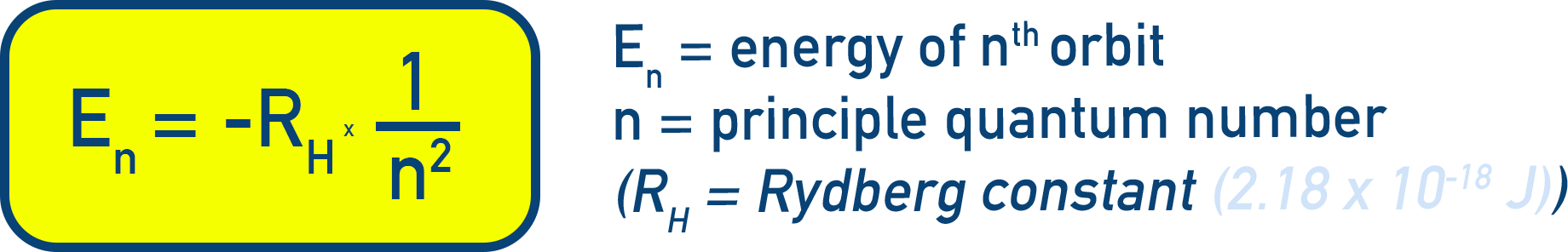
Note - the 1 in the formula comes from atomic number of hydrogen (given a positive charge from the nucleus of 1).
En = − 2.18 × 10−18 × (1 / n²) J
Meaning for E1 (lowest possible energy state) = − 2.18 × 10−18 J
Note:
- Negative energy indicates bound state – energy is required to free the electron.
- As n increases, energy becomes less negative (closer to zero), i.e., electron is less tightly bound.
For other species with only 1 electron (such as He+, Li2+, Be3+) we can use the following formula:
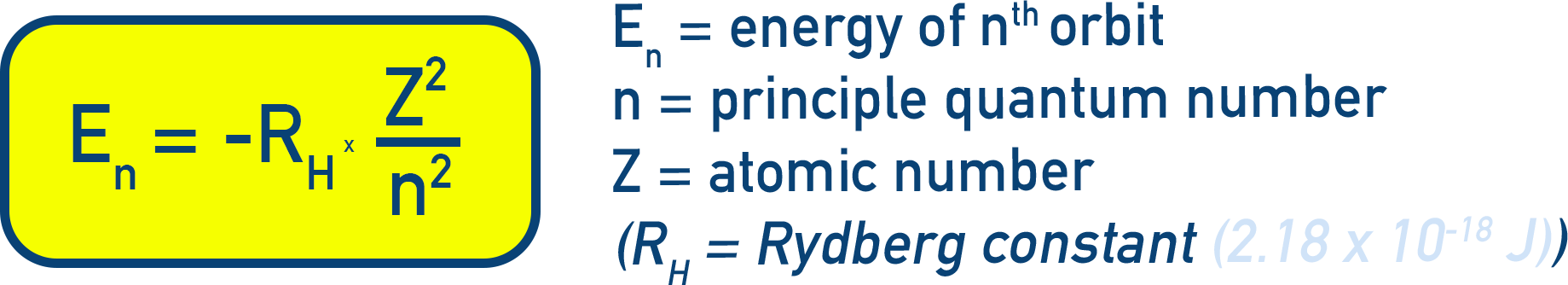
En = −2.18 × 10−18 × (Z² / n²) J (Equation 2.14)
As Z increases, the energy of the electron gets more negative. This means its harder to remove from the atom (or ion) in its stationary state.
The radii of an orbit can also be determined using:
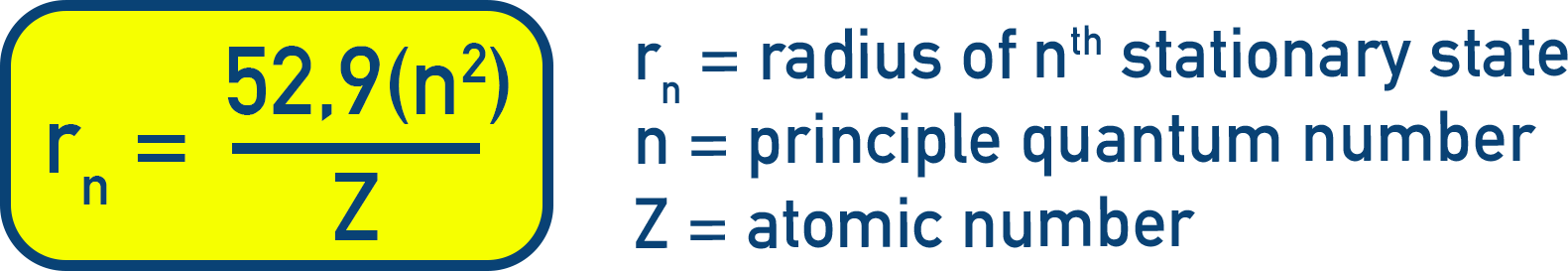
rn = 52.9 × (n² / Z) pm (Equation 2.15)
2.4.1 Explanation of Line Spectrum of Hydrogen
In hydrogen atoms, electrons don’t emit a continuous spectrum of light. Instead, we see a line spectrum – sharp, distinct lines of specific wavelengths. This is because electrons only occupy specific orbits with fixed energy, as Bohr proposed.
Why Do These Lines Appear?
- Electrons absorb energy to move from a lower energy level (nᵢ) to a higher one (n𝒇).
- When they return to lower energy levels, they release this energy as light (a photon).
- This energy change is quantized — only certain values are allowed. Hence, we see specific lines.
Energy of a Transition
When an electron moves from energy level nᵢ (initial) to n𝒇 (final), the energy difference is:
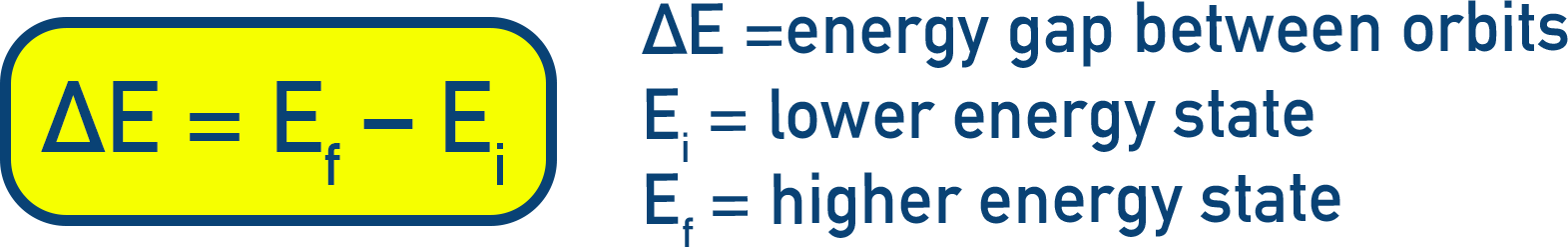
ΔE = E𝒇 – Eᵢ (Equation 2.16)
From Bohr’s model, the energy of each orbit is:
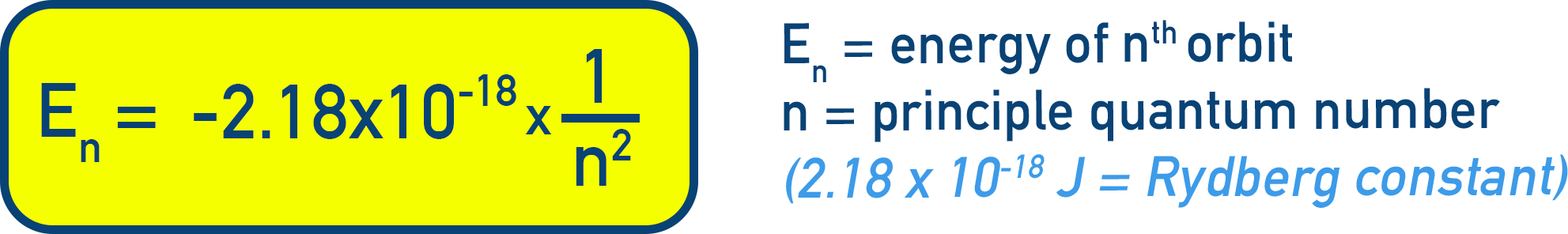
En = −2.18 × 10−18 × (1 / n²) J (Equation 2.13)
Substituting into ΔE gives:

ΔE = −2.18 × 10−18 × (1 / n𝒇² – 1 / nᵢ²) J (Equation 2.17)
- If nᵢ > n𝒇 (electron falls to lower orbit), ΔE is negative, and energy is emitted.
- If nᵢ < n𝒇 (electron rises), ΔE is positive, and energy is absorbed.
Frequency of Emitted or Absorbed Radiation
The frequency ν of the emitted or absorbed radiation is related to energy by Planck’s equation:

ν = ΔE / h (Equation 2.18)
Substituting ΔE from Equation 2.17:
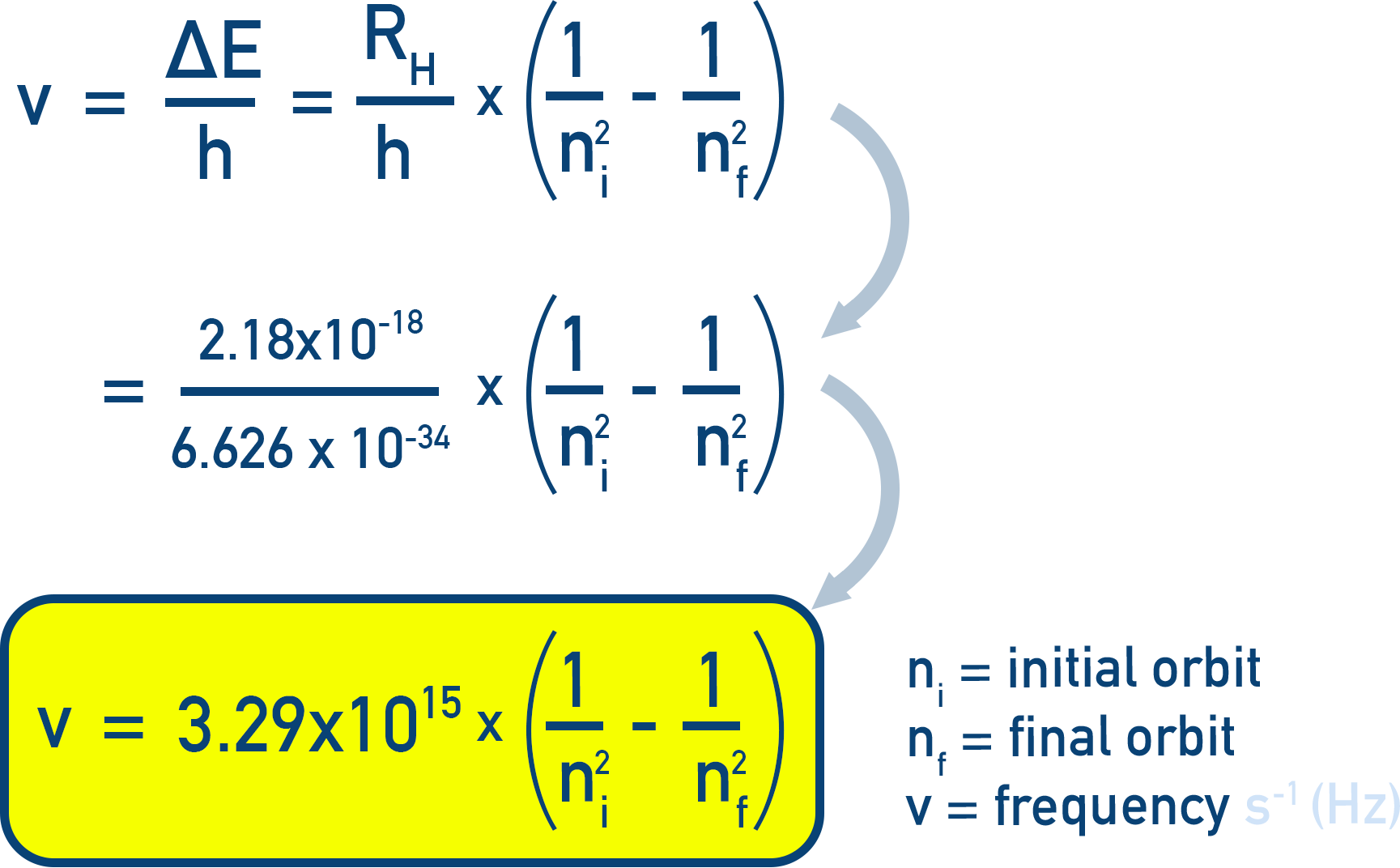
ν = RH × (1 / nᵢ² – 1 / n𝒇²) where RH = 3.29 × 1015 Hz (Equation 2.19)
This gives the frequency of the spectral line.
Wave Number (ṽ) and Line Spectrum
Wavenumber is the number of waves per unit length, and is defined as:
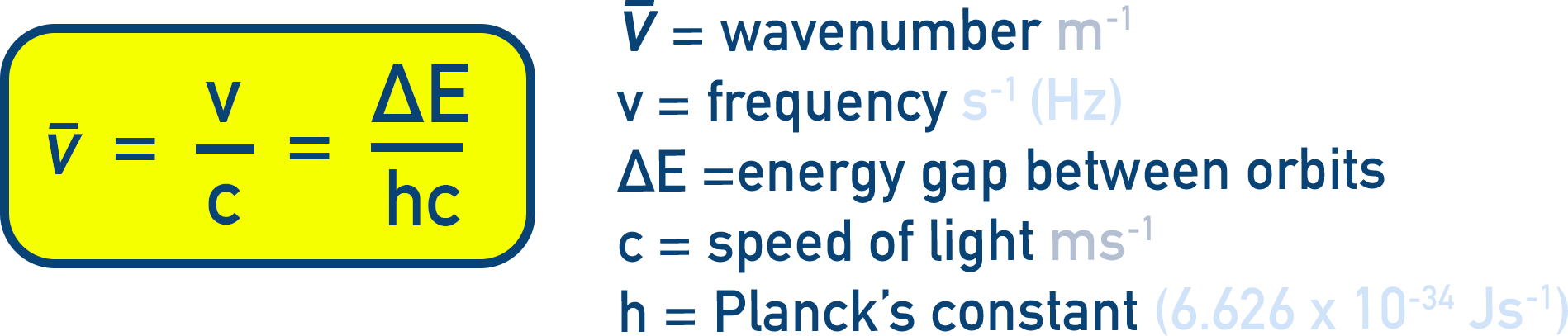
ṽ = ν / c = ΔE / (hc)
Substitute in the constants and formula for ΔE:
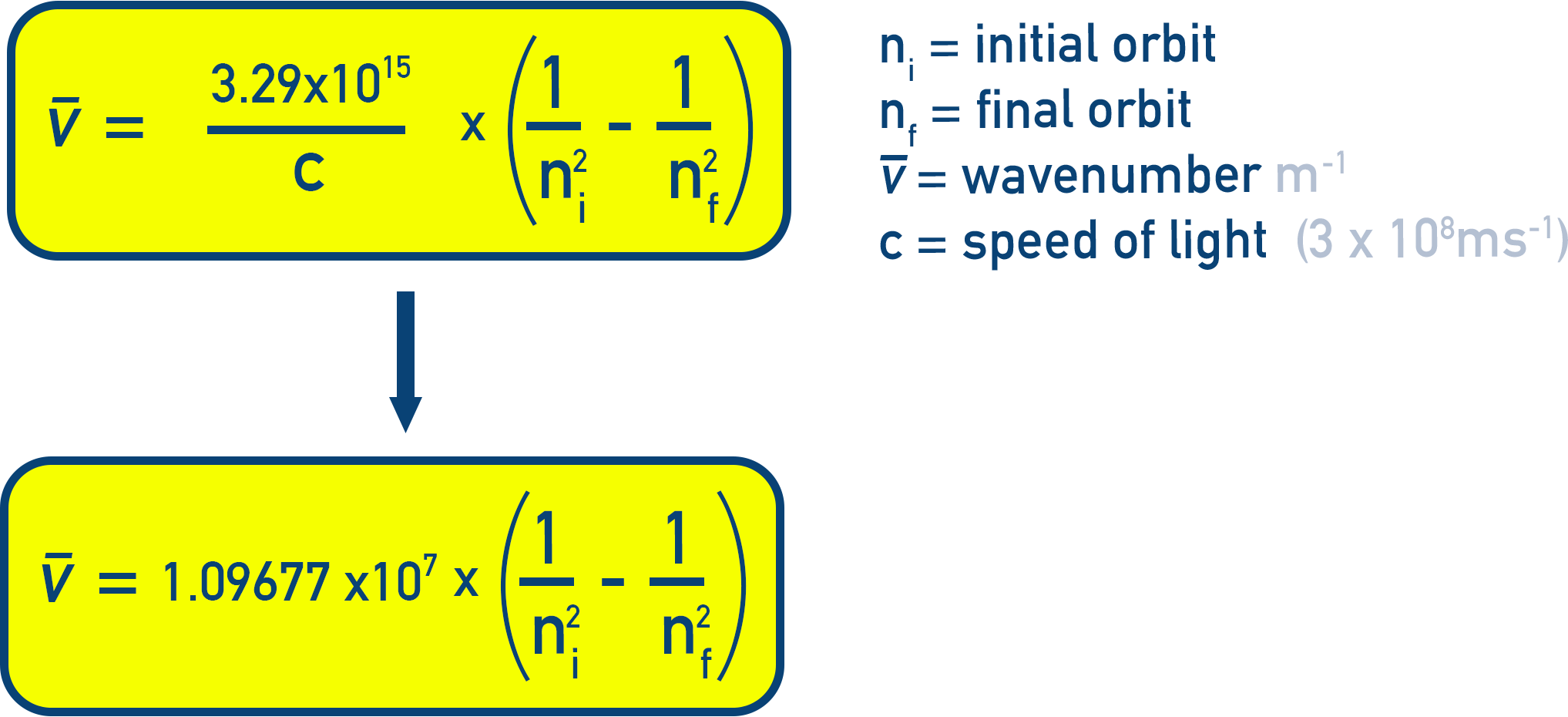
ṽ = RH / c × (1 / nᵢ² – 1 / n𝒇²)
ṽ = 1.09677 × 107 × (1 / nᵢ² – 1 / n𝒇²) m−1 (Equation 2.21)
This is the Rydberg formula, used to calculate wavelengths of spectral lines in hydrogen.
What to Remember
- Electrons move between stationary states (orbits).
- The light emitted corresponds to specific differences in energy.
- Negative ΔE → energy is released (emission)
- Positive ΔE → energy is absorbed
- As n increases, orbit energy becomes less negative → electron is less tightly bound.
- For hydrogen and other one-electron species (He+, Li2+), these equations apply directly.
Spectral Series of Hydrogen:
Each series corresponds to transitions ending at a specific lower level:

| Series Name | Final Level (n1) | Region of Spectrum |
|---|---|---|
| Lyman | 1 | Ultraviolet |
| Balmer | 2 | Visible |
| Paschen | 3 | Infrared |
| Brackett | 4 | Infrared |
| Pfund | 5 | Infrared |
Example Balmer emission
An electron falling from n = 3 to n = 2 → emits visible light (Balmer series).
2.4.2 Limitations of Bohr’s Model
Although successful for hydrogen, Bohr’s model fails in multiple ways:
- Could Not Explain Multi-Electron Systems
- Bohr’s equations and energy levels only apply to hydrogen or hydrogen-like ions (e.g. He+, Li2+)
- Spectra of more complex atoms do not fit Bohr’s model
- Spectral Fine Structure Not Explained
- Actual hydrogen spectral lines are split into multiple closely spaced lines (fine structure)
- Bohr's model predicts single lines only
- Fine structure is explained only by relativistic corrections and spin (quantum mechanics)
- Zeeman and Stark Effects Not Accounted For
- When atoms are placed in magnetic (Zeeman) or electric (Stark) fields, their spectral lines split further
- Bohr's model provides no explanation for these effects
- No Explanation for Heisenberg Uncertainty or Dual Nature
- Bohr treated electrons as particles in fixed orbits, ignoring their wave nature
- This contradicts the Heisenberg Uncertainty Principle, which says we can’t simultaneously know position and momentum of an electron exactly
- Incompatible with Quantum Mechanics
- Bohr’s model is semi-classical, using classical orbits with quantum jumps
- It violates modern quantum mechanics, which describes electrons as probability clouds (orbitals), not fixed orbits
Conclusion
Bohr’s model was a major breakthrough and laid the groundwork for quantum theory by introducing the idea of quantized energy levels. It successfully explained:
- Stability of hydrogen atom
- Line spectrum of hydrogen
- Rydberg formula derivation
But it failed to extend to multi-electron systems and did not incorporate the wave-particle duality, fine spectral features, or quantum mechanical principles, which were later addressed in more advanced models like Schrödinger’s.
Summary
- Bohr proposed quantized circular orbits with fixed energy.
- Electron transitions between levels produce spectral lines.
- Radius and energy depend on n and Z for one-electron species.
- Model works for hydrogen but not for multi-electron atoms.
- Modern quantum theory replaces fixed orbits with orbitals.
