Applications of Thermodynamic Concepts

Full Notes

5.2.1 Work — Pressure-Volume Work in Thermodynamics

What is Work in Thermodynamics?

In thermodynamics, the type of work usually considered is mechanical work, specifically pressure-volume (p–V) work. This is the work done when a gas is compressed or expanded in a cylinder fitted with a frictionless piston.

Work Done by a Gas at Constant External Pressure

When a gas is compressed or expanded under a constant external pressure (p_ex):

• Volume change:
  ΔV = V_f − V_i


• Work done:
  w = − p_ex × ΔV
  w = − p_ex × (V_f − V_i)


• Sign convention:
  • Work done on the system (compression): w > 0
  • Work done by the system (expansion): w < 0
  The negative sign follows the IUPAC convention.

Work When Pressure Is Not Constant

If external pressure changes in discrete steps during the process then:

• Total work done is the sum over all steps:
  w = − Σ (p × ΔV)

• This is represented as the shaded area under a pressure–volume graph.

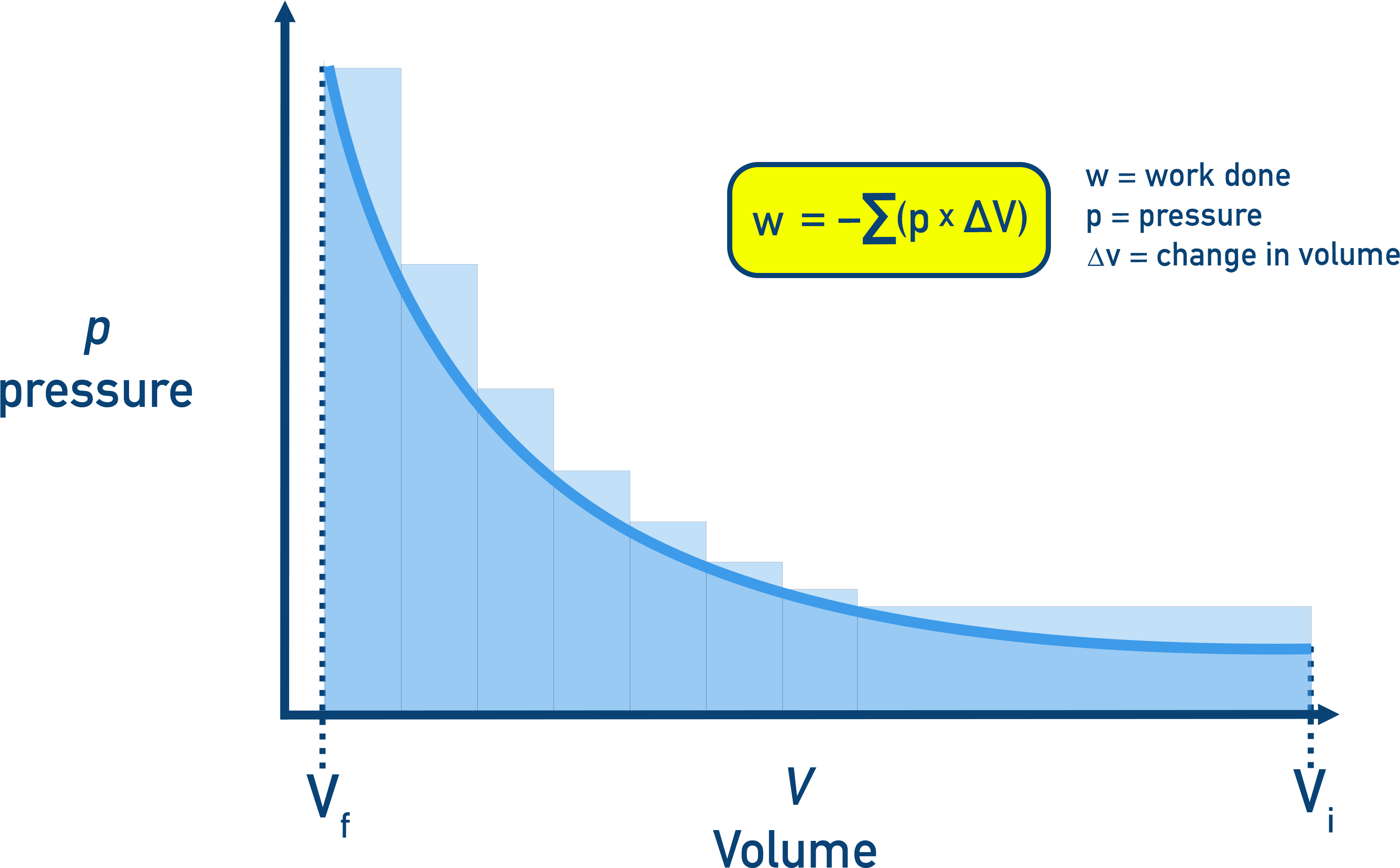
Reversible Processes

A reversible process occurs infinitely slowly such that the system remains in near-equilibrium with the surroundings at each step.

• Work expression for such a process:
  w = − ∫_Vi^V_f p_ex dV
• If pressure equals internal pressure (p_in), then:
  w_rev = − ∫_Vi^V_f p_in dV

Work in Terms of Ideal Gas Equation

For n moles of an ideal gas (pV = nRT), under isothermal and reversible conditions:

• w_rev = − nRT ln(V_f / V_i)
• Alternatively,
  w_rev = − 2.303 × nRT × log(V_f / V_i)

Free Expansion

When a gas expands into a vacuum:

• p_ex = 0
• w = 0 (no work is done)
• This is true whether the process is reversible or irreversible.

General Internal Energy Change

Using the First Law of Thermodynamics: ΔU = q + w

Substituting pressure–volume work: ΔU = q − p_ex × ΔV

At constant volume (ΔV = 0): ΔU = q_v
(where q_v denotes heat supplied at constant volume)

Isothermal and Free Expansion of an Ideal Gas

• Isothermal Expansion (Reversible):
  • Temperature remains constant
  • Work done is maximum for a given change in volume
  • Work formula: w = − nRT ln(V_f / V_i)
• Free Expansion:
  • Expansion in vacuum (no opposing pressure)
  • No work is done → w = 0
  • Common in Joule’s experiment

Key Points:

• Work is path-dependent (not a state function).
• Internal energy (U) is a state function.
• Pressure–volume work equals area under the p–V curve.
• No work is done in free expansion.
• Reversible processes yield the maximum amount of work.

5.2.2 Enthalpy, H

In most real-world chemical reactions, heat changes occur at constant pressure (e.g., in open beakers or flasks exposed to atmospheric pressure), not at constant volume. Under these conditions, we need a new thermodynamic quantity: enthalpy, denoted by H.

Definition of Enthalpy

• H is the enthalpy
• U is the internal energy
• p is pressure
• V is volume

It represents the total heat content of a system.

Relation Between Enthalpy and Internal Energy

Starting from the First Law: ΔU = q_p − pΔV (Equation 5.6)

Rewriting this: q_p = ΔU + pΔV

But since H = U + pV, we can write: ΔH = ΔU + pΔV (Equation 5.8)

Thus, at constant pressure, the heat absorbed by the system equals the change in enthalpy (ΔH): q_p = ΔH

Key Point: Enthalpy is a state function, like U, p, and V – it depends only on the initial and final states, not the path.

Enthalpy vs. Internal Energy

For reactions involving solids and liquids, the difference between ΔH and ΔU is usually negligible, since these substances undergo minimal volume change.

However, in gaseous reactions, pΔV becomes significant.

Using Ideal Gas Law

For a reaction involving gases, where:

• V_A = total volume of gaseous reactants
• V_B = total volume of gaseous products
• n_A = moles of gaseous reactants
• n_B = moles of gaseous products

Using pV = nRT, we get:

pΔV = (n_B − n_A)RT = Δn_g RT (Equation 5.9)

ΔH = ΔU + Δn_g RT (Equation 5.10)

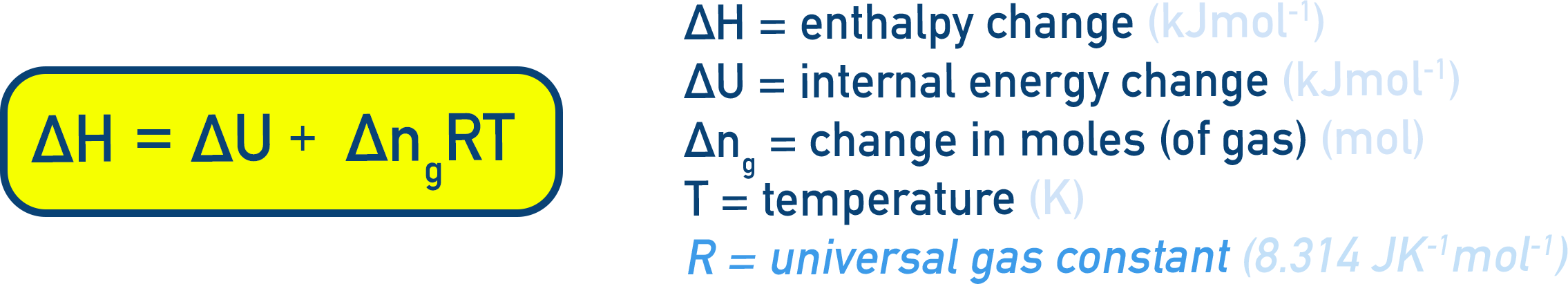
Where Δn_g = change in number of moles of gaseous species (products − reactants)

Signs of Enthalpy Change

• ΔH > 0 → Endothermic process (heat absorbed)
• ΔH < 0 → Exothermic process (heat released)

Important Notes

• q_p = ΔH only holds true at constant pressure.
• Enthalpy allows us to easily relate energy changes in chemical reactions under real laboratory conditions.
• Equation 5.10 is particularly useful when ΔU is known and gases are involved.

Extensive and Intensive Properties

Extensive Properties: Depend on the amount of matter
Examples: mass, volume, internal energy, enthalpy

Intensive Properties: Independent of quantity
Examples: temperature, pressure, density

Heat Capacity

Heat capacity (C) defines how much heat is needed to raise temperature of a system.

• Heat capacity (C): q = C × ΔT
• Molar heat capacity: Heat needed to raise the temperature of 1 mole of substance
• Specific heat (c): Heat required per gram per degree rise in temperature

Relationship:

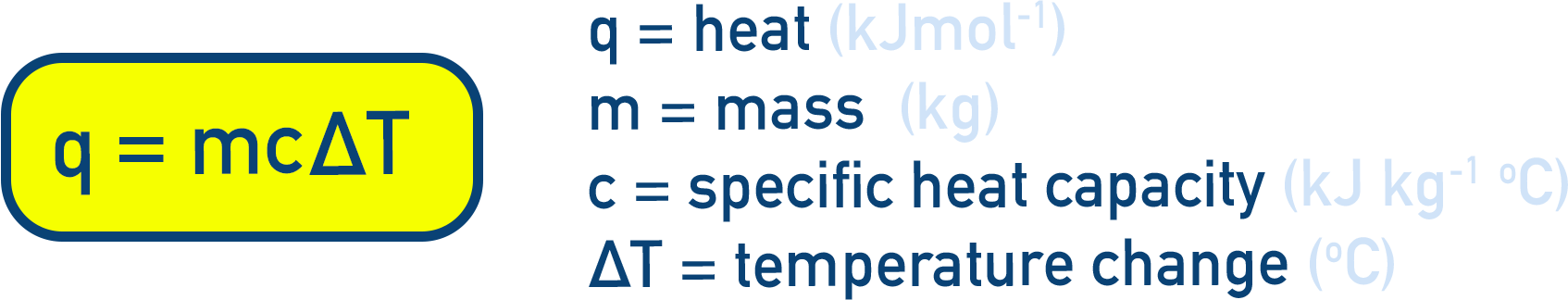
The Relationship between C_p and C_v for an Ideal Gas

Heat Capacities

• At constant volume, heat capacity is denoted by C_v.
• At constant pressure, it is denoted by C_p.
• These values represent the amount of heat required to raise the temperature of 1 mole of gas by 1 K at constant volume or pressure.

Basic Equations

• At constant volume (ΔV = 0): q_v = C_v × ΔT = ΔU
  (Since there is no expansion work, all the heat goes into increasing internal energy.)
• At constant pressure: q_p = C_p × ΔT = ΔH
  (Some of the heat is used to do expansion work, so more heat is required to achieve the same temperature change.)

Deriving the Relationship Between C_p and C_v

For 1 mole of an ideal gas, the enthalpy change can be written as:

ΔH = ΔU + Δ(pV)

Using the ideal gas equation (pV = nRT for 1 mole, so pV = RT), we get:

ΔH = ΔU + Δ(RT) → ΔH = ΔU + R × ΔT

Substituting into Heat Capacity Expressions

C_p × ΔT = C_v × ΔT + R × ΔT

Divide both sides by ΔT:

C_p = C_v + R

So the relationship is:

Summary

• Work and heat are path dependent and pressure–volume work equals area under the p–V curve.
• Free expansion does no work and reversible processes give maximum work.
• Enthalpy H equals U plus pV and at constant pressure heat = ΔH.
• Heat capacity links heat to temperature change with q = m × c × ΔT.
• For ideal gases Cp minus Cv = R.