Applications of Equilibrium Constants
Quick Notes
- K (equilibrium constant) indicates how far a reaction proceeds.
- Extent of Reaction:
- Very large K (K ≫ 1): Reaction proceeds nearly to completion.
- Very small K (K ≪ 1): Hardly any reaction occurs.
- Direction of Reaction:
- We can predict the direction a reaction will proceed in using the reaction quotient Q:
- Q < K → Forward reaction favored
- Q > K → Reverse reaction favored
- Q = K → At equilibrium
- Equilibrium Concentrations: ICE tables can be used to calculate unknown equilibrium concentrations.
Full Notes
Applications of Equilibrium Constants
Before looking at how to use equilibrium constants in practice, let’s first recap a few important characteristics of them:
Key Features of Equilibrium Constants
- Applies at Equilibrium Only
- The expression for an equilibrium constant is valid only when the system has reached equilibrium, meaning the concentrations of reactants and products have stabilized.
- Independent of Initial Concentrations
- The value of the equilibrium constant depends only on the reaction and temperature, not on how much of each substance you started with.
- Temperature Dependent
- For any specific reaction, the value of the equilibrium constant changes if the temperature changes.
- Reversing a Reaction Inverts K
- If you reverse the direction of a reaction, the new equilibrium constant is simply the reciprocal (1/K) of the original.
- Multiplying the Equation Affects K
- If you multiply the entire balanced reaction by a number, raise K to that power.
(e.g., if you double the reaction, new K = K2)
- If you multiply the entire balanced reaction by a number, raise K to that power.
We can use equilibrium constants to:
- Predict how far a reaction will proceed (its extent).
- Predict the direction in which a reaction will shift.
- Calculate concentrations at equilibrium.
6.6.1 Predicting the Extent of a Reaction
The magnitude of K tells us how "complete" a reaction is – but it doesn't tell us how fast it reaches equilibrium.
- Kc or Kp is large: High concentration of products at equilibrium.
- Kc or Kp is small: High concentration of reactants at equilibrium.
This helps us judge whether a reaction will go close to completion (high concentration of products) or hardly proceed (high concentration of reactants).
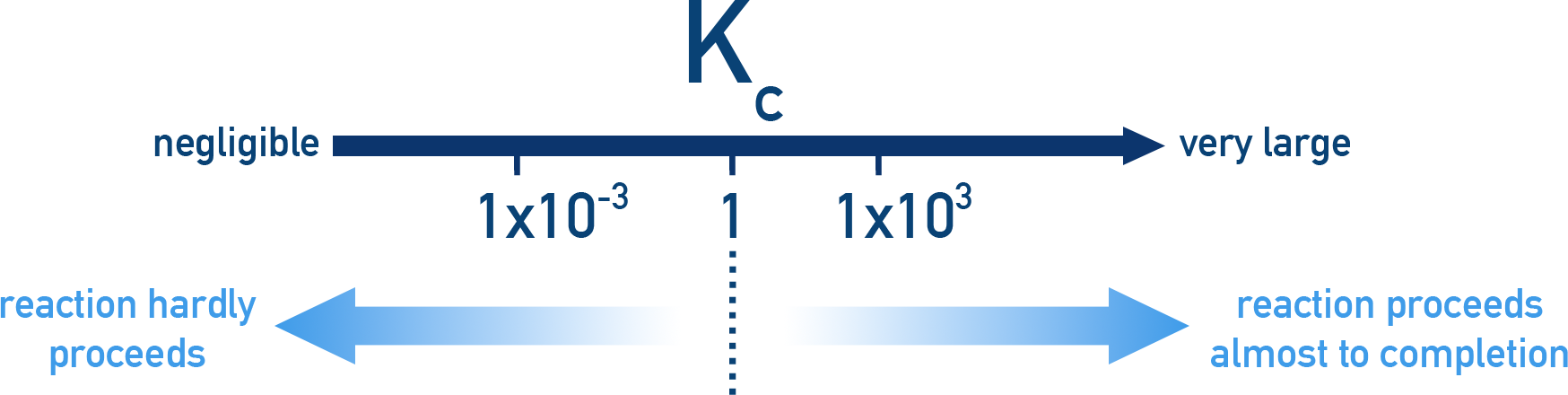
- K ≫ 103: Reaction goes nearly to completion (product-favoured).
- K ≈ 1: Comparable amounts of reactants and products.
- K ≪ 10−3: Reaction barely proceeds (reactant-favoured).
6.6.2 Predicting the Direction of the Reaction
What is the Reaction Quotient (Q)?
The reaction quotient (Q) is a snapshot of a reaction’s progress. It is calculated by using concentration values at a specific point in time, which might not be equilibrium values (unlike for Kc and Kp).
General formula for a reaction:


Comparing Q and K
The reaction quotient (Q) can be compared to the equilibrium constant (K) to predict the direction in which a reversible reaction will proceed.
It’s important to compare like with like – for example, Qc must be compared with Kc, and Qp with Kp. Mixing types (e.g., comparing Qc with Kp) is not valid.
- If Q = K, the system is at equilibrium. The rates of the forward and reverse reactions are equal, and the concentrations of all species remain constant.
- However, If Q ≠ K, the system is not at equilibrium. The reaction will proceed in the direction that moves Q toward K.
| Comparison | Interpretation | Shift Direction |
|---|---|---|
| Q < K | Too many reactants, not enough products | Shift right (products) |
| Q > K | Too many products, not enough reactants | Shift left (reactants) |
| Q = K | System is already at equilibrium | No shift |
For the reaction: N2(g) + 3H2(g) ⇌ 2NH3(g) the equilibrium constant K = 0.50 at a given temperature. At one point during the reaction, the concentrations are: [N2] = 0.20 mol dm−3, [H2] = 0.60 mol dm−3, [NH3] = 0.10 mol dm−3.
Using this information: calculate the reaction quotient Q and determine the direction in which the reaction will shift to reach equilibrium.
- Write the expression for Q
Q = \[NH3\]2 / \(\[N2\]\[H2\]3\) - Substitute the concentrations
Q = (0.10)2 / \(\,0.20 × 0.603\,\)
Q = 0.01 / \(0.20 × 0.216\) = 0.01 / 0.0432 ≈ 0.231 - Compare Q with K
Q ≈ 0.231, K = 0.50 → Q < K - Decide the shift
Since Q < K, the reaction will proceed in the forward direction to form more NH3 until equilibrium is reached.
Answer: Q ≈ 0.231. Because Q < K, the system shifts right (forward), favouring formation of more NH3.
6.6.3 Calculating Equilibrium Concentrations
You need to be able to determine equilibrium concentrations, to do this we can use ICE tables.
- Write the balanced equation.
- Fill in Initial concentrations.
- Use ‘x’ to denote Change.
- Express Equilibrium concentrations.
- Substitute into K expression and solve.
For the reaction: H2(g) + I2(g) ⇌ 2HI(g) At 298 K, the equilibrium constant is K = 50.0. At equilibrium: [HI] = 0.80 mol dm−3 [I2] = 0.10 mol dm−3 Calculate the equilibrium concentration of H2.
- Step 1: Use an ICE table
Let the change in [HI] be +2x, so [HI] = 0.80 → x = 0.40.
The change in [H2] and [I2] is −x = −0.40.Species Initial Change Equilibrium H2 a −0.40 a − 0.40 I2 — −0.40 0.10 HI 0 +0.80 0.80 - Step 2: Apply the equilibrium expression
K = [HI]2 / ([H2][I2])
50.0 = (0.80)2 / [(a − 0.40)(0.10)]
50.0 = 0.64 / [0.10(a − 0.40)]
0.10(a − 0.40) = 0.64 / 50 = 0.0128
a − 0.40 = 0.128
a = 0.528 mol dm−3 - Step 3: Final answer
[H2] at equilibrium = a − 0.40 = 0.128 mol dm−3
Summary
- K indicates reaction extent at a given temperature.
- Compare Q with K to predict shift direction.
- Use ICE tables with K to find unknown equilibrium concentrations.
- Reversing or scaling an equation changes the reported K accordingly.
