Developments Leading to the Bohr’s Model of Atom

Full Notes:

Models to describe atomic structure have changed over time, based on experimental data and observations.

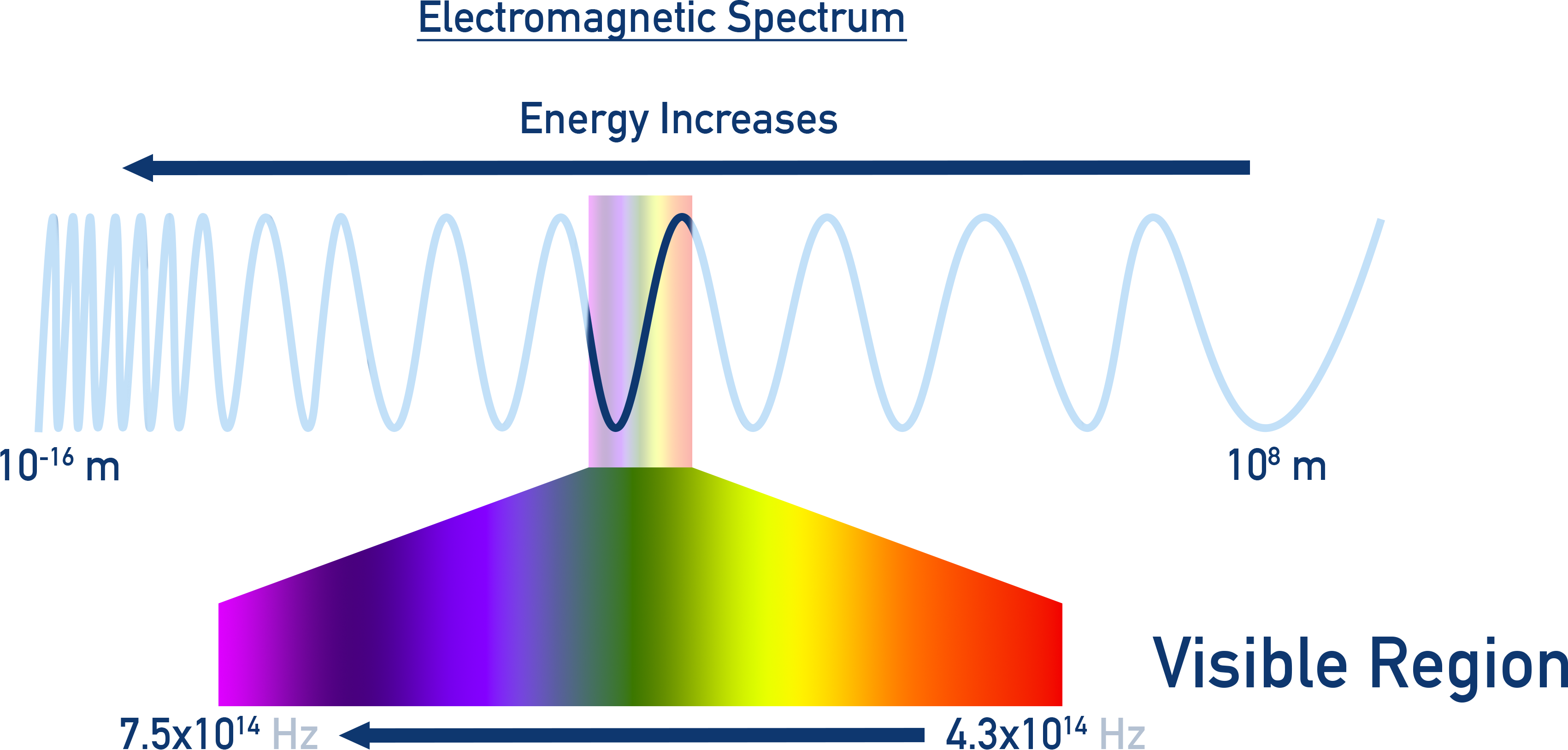
2.3.1 Wave Nature of Electromagnetic Radiation

Electromagnetic radiation (EMR) is a form of energy that moves through space as oscillating electric and magnetic fields, perpendicular to each other and to the direction of the wave.

Key characteristics of waves:

• Wavelength (λ): Distance between two consecutive peaks or troughs (in meters).
• Frequency (ν): Number of wave cycles per second (in s⁻¹ or Hz).
• Amplitude: Height of the wave; related to the intensity of the radiation.
• Velocity (c): Speed of light in vacuum = 3.0 × 10⁸ m/s.

Relationship:

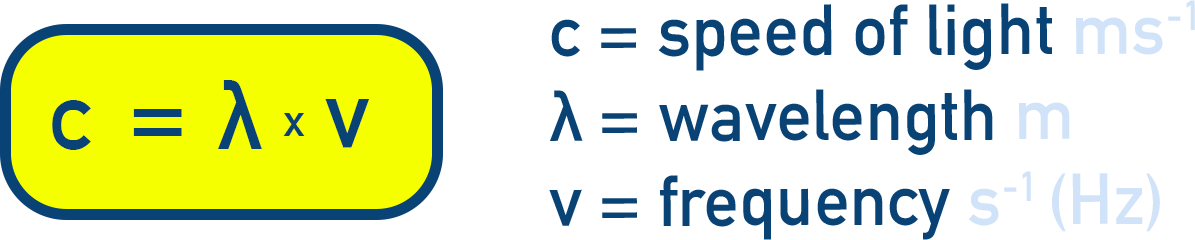
c = ν × λ  (Equation 2.5)

Different types of EMR (radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, gamma rays) vary in their wavelengths and frequencies but all travel at the same speed (c).

2.3.2 Planck’s Quantum Theory

Classical physics predicted that atoms should emit or absorb energy continuously. However, experimental observations such as black body radiation did not match this.

Planck’s Proposal (1900):

• Energy is not continuous, but quantized.
• Atoms emit or absorb energy in discrete packets called quanta.
• Each quantum of energy is related to frequency:

E = h × ν  (Equation 2.6)

Where:

• E = energy (in joules)
• h = Planck’s constant = 6.626 × 10⁻³⁴ J·s
• ν = frequency of radiation

If radiation has a higher frequency (e.g., ultraviolet), each quantum carries more energy.

Photoelectric Effect

The photoelectric effect was discovered by Hertz and later explained by Einstein (1905):

When light of sufficient frequency falls on a metal surface, electrons are ejected from it.

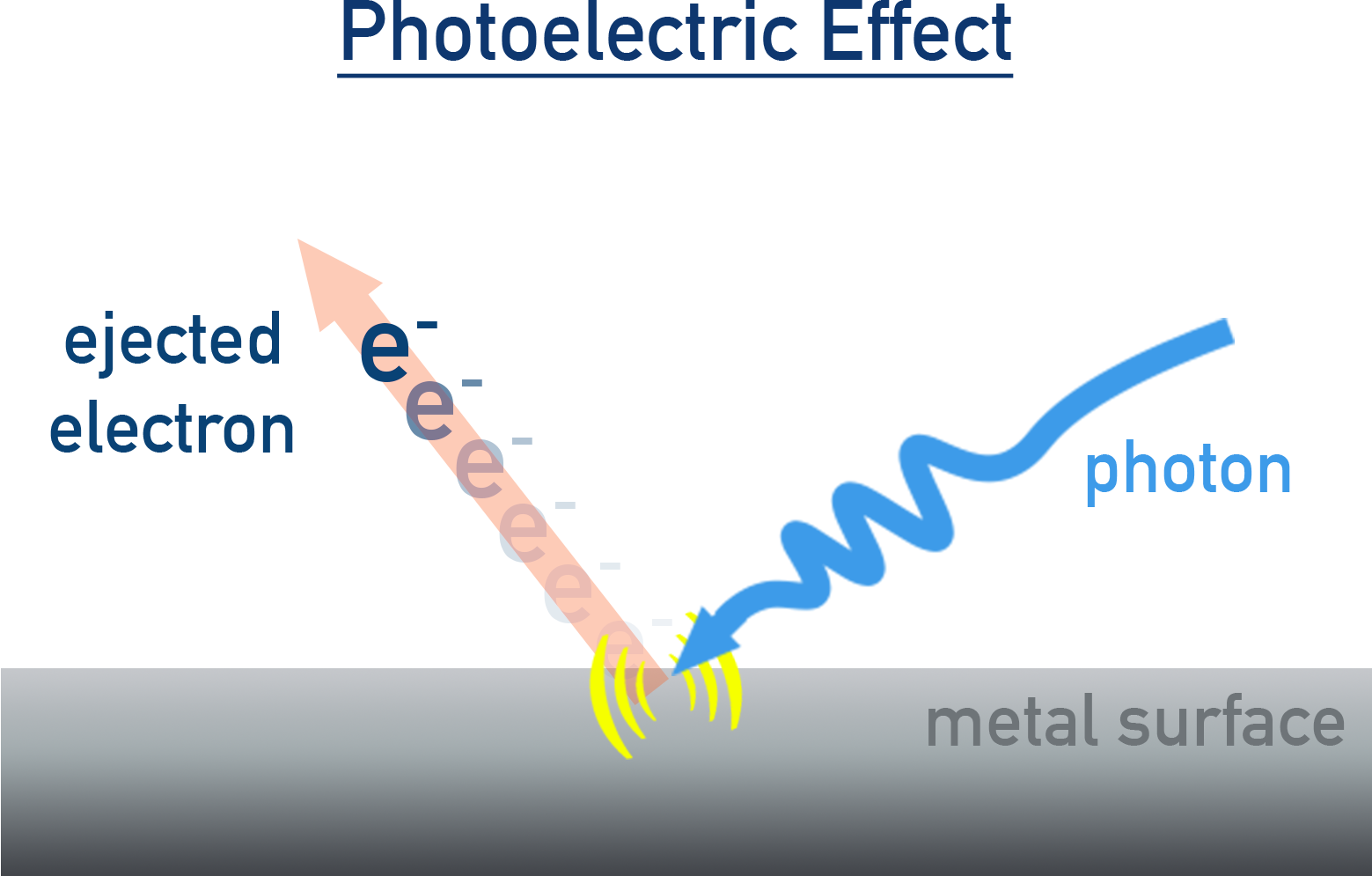
Key observations:

• Electrons are only emitted if light has frequency above a threshold frequency (ν₀).
• Below ν₀, no electrons are ejected regardless of intensity.
• Number of electrons depends on intensity.
• Kinetic energy of electrons depends on frequency.

Einstein’s Explanation:

• Light consists of photons (particles of light).
• Each photon has energy E = h × ν.
• Energy of photon is used to overcome work function (W₀) of metal, remaining energy appears as kinetic energy (K.E.).

The kinetic energy of ejected electrons is described by:

hν = hν₀ + (1/2) mₑv²  (Equation 2.7)

This confirmed that light behaves like particles, not just waves.

Dual Behaviour of Electromagnetic Radiation

Electromagnetic radiation behaves both as:

• Waves (interference, diffraction)
• Particles (photoelectric effect, black body radiation)

This is called wave-particle duality.

Planck and Einstein showed that light must be treated as discrete packets of energy (photons) in some cases, and as waves in others.

2.3.3 Evidence for Quantized Electronic Energy Levels: Atomic Spectra

Atoms emit radiation only at certain wavelengths when excited, forming a line spectrum, not a continuous one.

This indicates that electrons can only occupy discrete energy levels, and transitions between them release quanta of energy.

Emission and Absorption Spectra

When an atom absorbs energy (e.g., from heat or electricity), its electrons jump to higher energy levels – this is called the excited state.

But electrons don’t stay excited forever. They soon fall back to lower energy levels, releasing energy as light (photons).

Each jump from one energy level to another releases a photon of a specific energy, which corresponds to a specific wavelength and colour of light.

The result is an emission spectrum – a set of bright lines against a dark background, each one representing a specific transition.

• Emission spectrum: Formed when atoms emit light after excitation and seen as bright lines on a dark background.
• Absorption spectrum: Formed when atoms absorb certain wavelengths from white light and seen as dark lines on a continuous spectrum.

These spectra are element-specific and act as "atomic fingerprints".

Line Spectrum of Hydrogen

Hydrogen emits light at discrete wavelengths (visible lines = Balmer series).

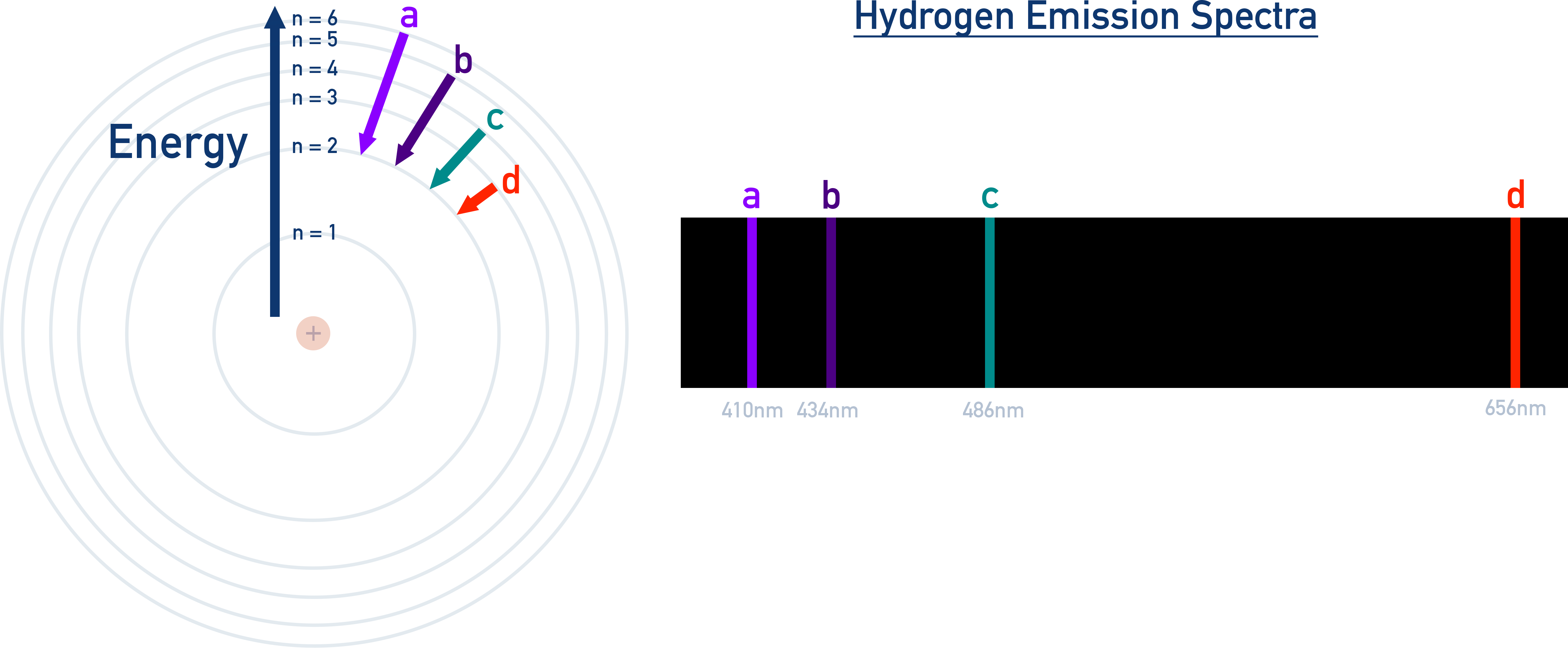
This cannot be explained by classical physics.

However, Balmer series emission energies can be described by the Rydberg formula for hydrogen spectral lines:

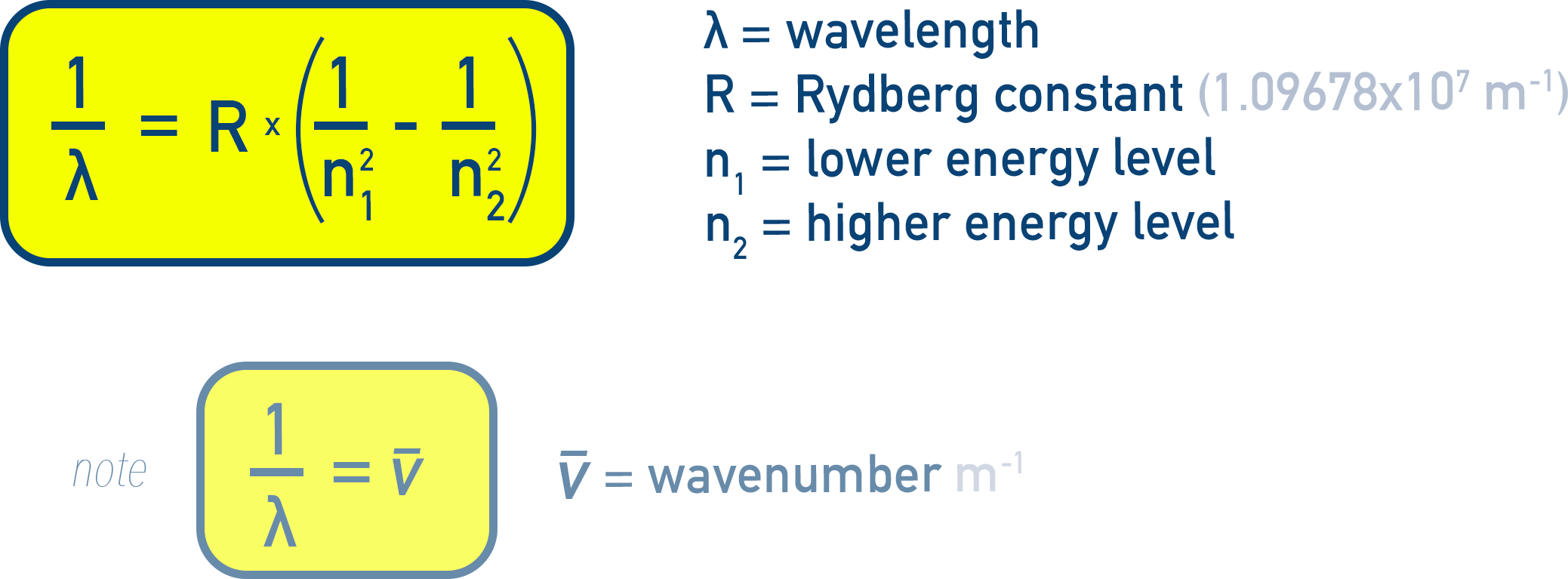
ṽ = 109,677 × (1 / 2² – 1 / n²) cm⁻¹  (Equation 2.8)

Where:

• λ = wavelength of emitted light
• R = Rydberg constant = 1.09678 × 10⁷ m⁻¹
• n₁ = lower energy level (fixed)
• n₂ = higher energy level (n₂ > n₁)

For the Balmer series: n₁ = 2, n₂ = 3, 4, 5, …

This strongly supports that electrons exist in quantized orbits, with transitions between them producing specific spectral lines.

Spectral line series:

Transitions to different energy levels (to n=1, n=2 and n=3) emit wavelengths of different types of electromagnetic radiation.

• When electrons fall to n = 1, emitted wavelengths are in UV region (Lyman Series).
• When electrons fall to n = 2, emitted wavelengths are in visible region (Balmer Series).
• When electrons fall to n = 3, emitted wavelengths are in IR region (Paschen Series).

Matt’s exam tip

Use E = h × ν = h × c / λ for energy-related problems. The photoelectric effect proves the particle nature of light. Emission spectra involve electrons releasing energy; absorption spectra involve electrons absorbing energy. The hydrogen spectrum provides direct evidence of quantized energy levels.

Summary

• Light behaves as both wave and particle (wave–particle duality).
• Planck introduced quantized energy emission; Einstein confirmed it through the photoelectric effect.
• Energy of a photon depends on its frequency (E = hν).
• Atomic spectra reveal discrete energy levels for electrons.
• Hydrogen’s line spectrum confirmed the existence of quantized orbits and led to Bohr’s model.