Enthalpies for Different Types of Reactions
Quick Notes
- Standard enthalpy of combustion, ΔcH°: heat released during complete combustion of one mole of substance.
- Enthalpy of atomisation, ΔaH° : energy required to produce one mole of gaseous atoms.
- Bond enthalpy, ΔbondH°: energy to break one mole of bonds in the gaseous state.
- Lattice enthalpy – Heat change when gaseous ions form an ionic solid (or the reverse).
- Enthalpy of solution, ΔsolH°: enthalpy change when one mole of solute dissolves.
- Enthalpy of dilution – Heat change when a solution is further diluted with solvent.
Full Notes
Introduction
Enthalpy changes depend on the type of process occurring during a chemical or physical transformation. These include breaking chemical bonds, forming new ones, mixing solutes and solvents, or changing phases. Each process is associated with a specific type of enthalpy change, measured under standard conditions (usually 298 K and 1 atm), and represented by a unique symbol.
Standard Enthalpy of Combustion (ΔcH°)
Defined as the enthalpy change when one mole of a substance is completely burnt in oxygen under standard conditions.
- Products are usually CO2(g) and H2O(l) for organic compounds.
- Always exothermic (ΔcH° is negative).
Example: Methane combustion
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l)
ΔcH° = −890.3 kJ mol⁻¹
Enthalpy of Atomisation (ΔaH°)
The enthalpy change when one mole of gaseous atoms is formed from the element in its standard state.
- Always positive, as energy is required to break bonds.
Examples: Sodium and chlorine
- Na(s) → Na(g); ΔaH° = +108.4 kJ mol⁻¹
- ½Cl2(g) → Cl(g); ΔaH° = +121.7 kJ mol⁻¹
For diatomic molecules like Cl2, only half a mole is needed to form one mole of atoms.
Bond Enthalpy (ΔbondH°)
Bond Enthalpy
In thermodynamics, enthalpy changes associated with bond breaking and bond making are categorized into two main types:
- Bond dissociation enthalpy
- Mean bond enthalpy
Diatomic Molecules
For diatomic molecules, bond dissociation enthalpy refers to the enthalpy change when one mole of covalent bonds in a gaseous covalent compound is broken to form gaseous atoms.
Example: H–H bond
H2(g) → 2H(g) ΔHH–H° = 435.0 kJ mol⁻¹
Examples: Other diatomics
- Cl2(g) → 2Cl(g) ΔHCl–Cl° = 242 kJ mol⁻¹
- O2(g) → 2O(g) ΔHO=O° = 428 kJ mol⁻¹
This value is both the bond dissociation enthalpy of the H–H bond and the enthalpy of atomization of hydrogen gas.
Polyatomic Molecules
In polyatomic molecules, the energy required to break each bond can vary due to differences in the molecular environment. Hence, we use mean bond enthalpy.
Example: Methane (CH4)
Overall atomization reaction: CH4(g) → C(g) + 4H(g) ΔHa° = 1665 kJ mol⁻¹
- CH4(g) → CH3(g) + H(g); ΔH° = 427 kJ mol⁻¹
- CH3(g) → CH2(g) + H(g); ΔH° = 439 kJ mol⁻¹
- CH2(g) → CH(g) + H(g); ΔH° = 452 kJ mol⁻¹
- CH(g) → C(g) + H(g); ΔH° = 347 kJ mol⁻¹
- Total ΔH° = 1665 kJ mol⁻¹
So, mean bond enthalpy of C–H = ΔHC–H° = (1/4) × ΔHa° = (1/4) × 1665 = 416 kJ mol⁻¹
Note: Mean bond enthalpies may differ slightly across compounds but do not vary significantly.
Using Bond Enthalpies to Calculate Reaction Enthalpy
The standard enthalpy of reaction, ΔHr°, can be estimated using bond enthalpies with the formula:

This formula gives the net enthalpy change of a reaction and is particularly useful when ΔHr° values are not available.
Note - This approach is valid when all substances involved are in the gas phase, and the relationship is approximate.
Lattice Enthalpy
Lattice Enthalpy is defined as the enthalpy change when one mole of an ionic solid dissociates into its gaseous ions (or vice versa).
- When forming a lattice from ions → exothermic
- When breaking a lattice into ions → endothermic
Examples: NaCl lattice formation and dissociation
- Na+(g) + Cl−(g) → NaCl(s); ΔH = −787 kJ mol⁻¹
- NaCl(s) → Na+(g) + Cl−(g); ΔH = +787 kJ mol⁻¹
Lattice enthalpy is a measure of ionic bond strength and affects melting point and solubility.
Lattice enthalpies can’t be measured directly experimentally, however, they can be found indirectly using Born–Haber cycles.
Born-Haber Cycles
A Born–Haber cycle breaks down the formation of an ionic compound into a series of theoretical steps. It applies Hess’s Law to calculate one unknown energy change (often lattice enthalpy or enthalpy of formation).
Each step corresponds to a real or theoretical process in forming the ionic solid from its elements in standard states.
Standard Born–Haber cycles often include:
- Enthalpy of Formation (ΔHf)
Energy change when 1 mole of an ionic compound forms from its elements in standard states.
Example: Na (s) + ½Cl2 (g) → NaCl (s) - Enthalpy of Atomisation (ΔHatom)
Energy change when 1 mole of gaseous atoms forms from an element.
Example:Na (s) → Na (g) | ½Cl2 (g) → Cl (g) - 1st Ionisation Energy (IE)
Energy required to remove 1 mole of electrons from 1 mole of gaseous atoms of an element (to form 1 mole’s worth of ions with a 1+ charge).
Example:Na (g) → Na+ (g) + e− - Bond Enthalpy
Energy required to break one mole’s worth of a covalent bond in gaseous molecules.
Example:Cl2 (g) → 2Cl (g) - 1st Electron Affinity (EA)
Energy change when 1 mole of gaseous atoms gains electrons to form 1 mole’s worth of ions with a 1− charge.
Example:Cl (g) + e− → Cl− (g) - Lattice Enthalpy (ΔHlef or ΔHled)
Energy change when 1 mole of an ionic lattice forms or dissociates from gaseous ions. This is often the unknown value we solve for.
Example: Born–Haber Cycle for NaCl
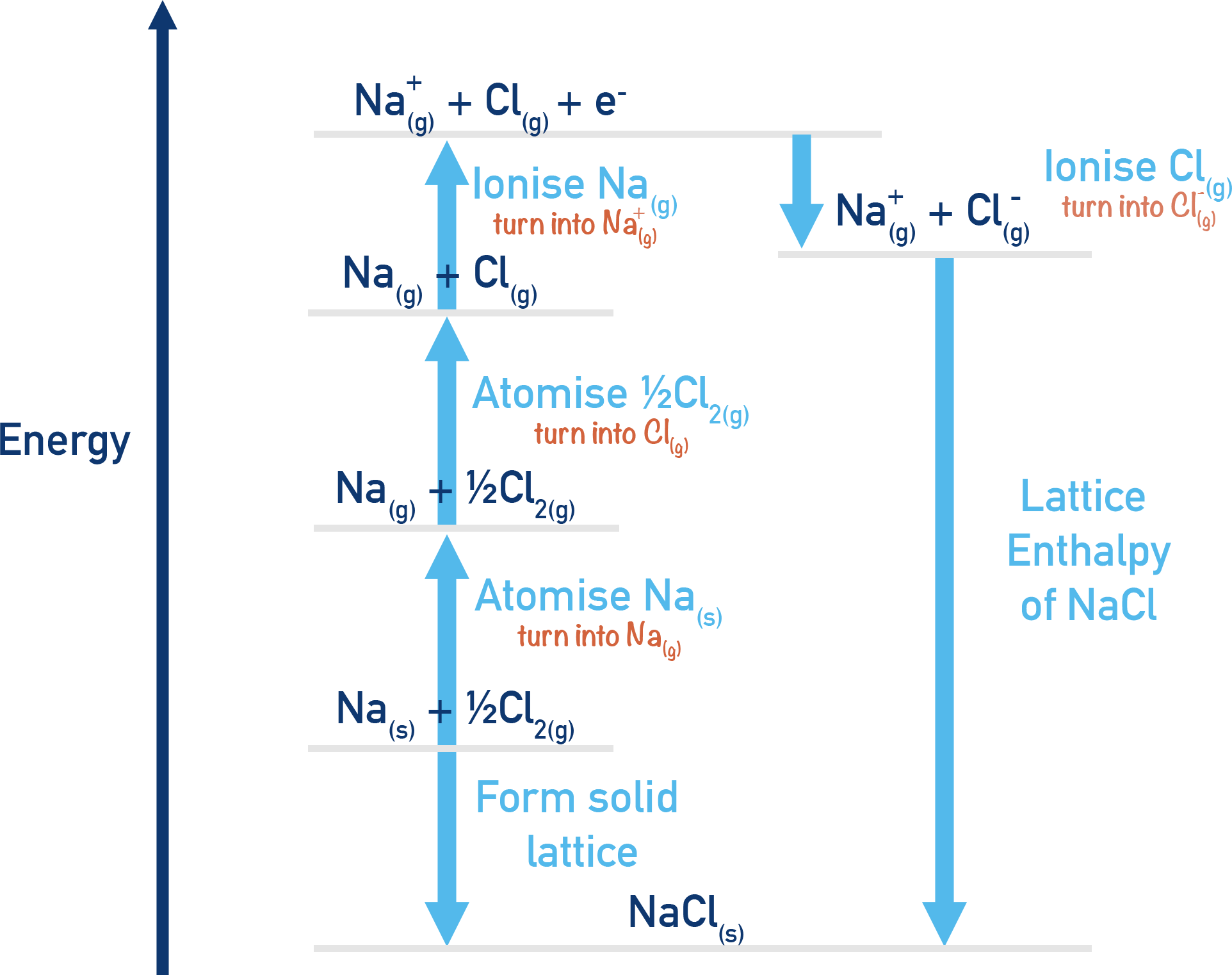
Step 1: Formation of NaCl (ΔHf) Na (s) + ½Cl2 (g) → NaCl (s)
Step 2: Atomisation of Na (ΔHatom) Na (s) → Na (g)
Step 3: Atomisation of Cl2 (ΔHatom) ½Cl2 (g) → Cl (g)
Step 4: Ionisation Energy of Na (IE1) Na (g) → Na+ (g) + e−
Step 5: Electron Affinity of Cl (EA1) Cl (g) + e− → Cl− (g)
Step 6: Lattice Enthalpy (ΔHle) Na+ (g) + Cl− (g) → NaCl (s)
By rearranging these enthalpy changes and substituting experimental values into the cycle we can use Hess’s Law to calculate ΔHle.
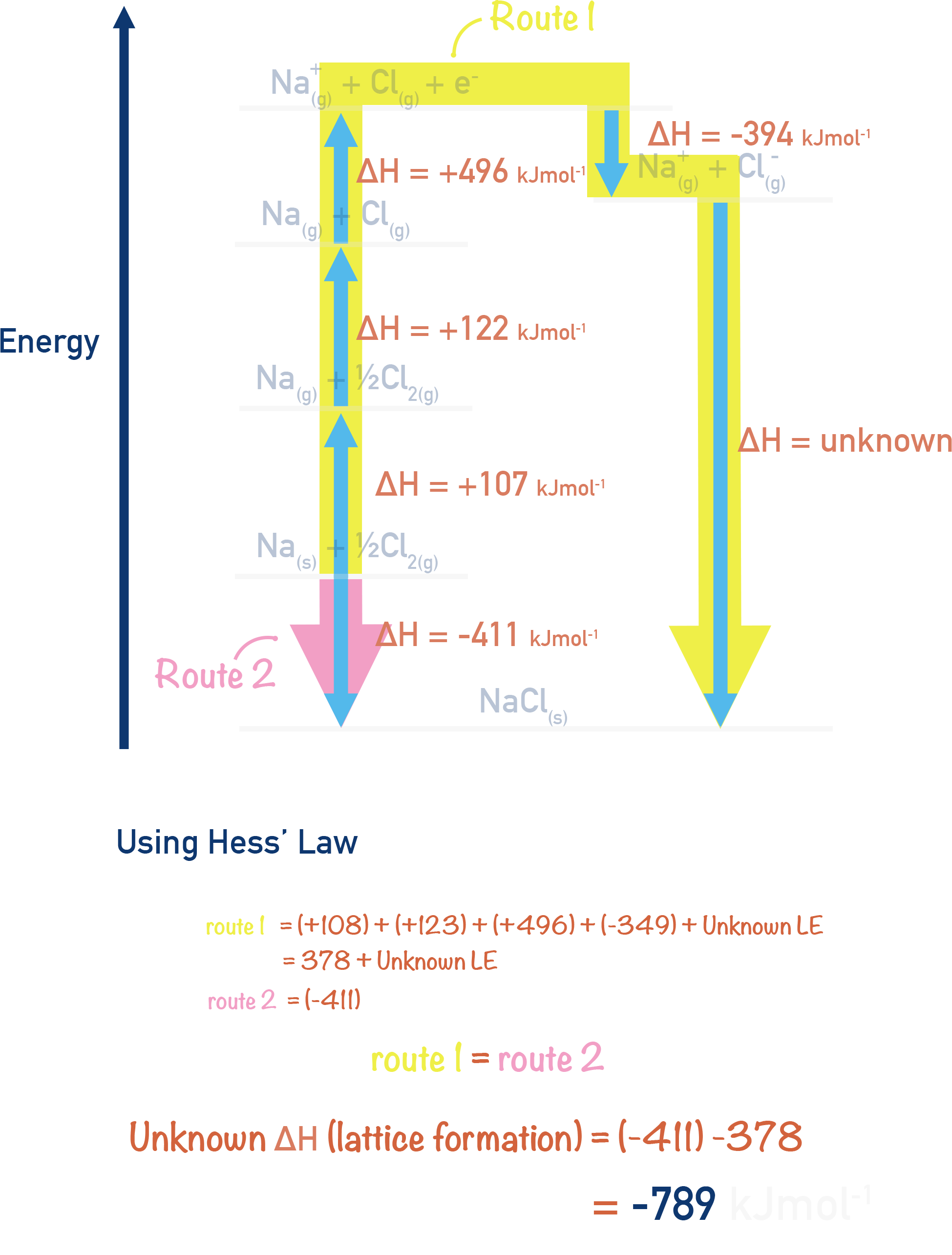

For these energy cycles, the lattice energy is given as a positive value as the arrow direction is going from the ionic solid to the gaseous ions, this is breaking apart the lattice. This is the exact same value as lattice energy however it has a positive sign (+ΔH) rather than negative as it is an endothermic process.
Enthalpy of Solution (ΔsolH°)
Enthalpy of Solution (ΔsolH°) is the enthalpy change when 1 mole of solute dissolves in excess solvent so that further dilution causes no significant heat change.
- Can be positive (endothermic) or negative (exothermic) depending on balance between lattice energy and hydration enthalpy.
Example: KCl dissolution
KCl(s) → K+(aq) + Cl−(aq); ΔsolH° = +18.6 kJ mol⁻¹ (NCERT Example)
Positive ΔsolH° indicates that dissolution absorbs heat.
Energy Cycle for Solution Enthalpy
An energy cycle can be constructed that links enthalpy of solution (ΔHsol), hydration enthalpies (ΔHhyd) and lattice energy (ΔHlatt):
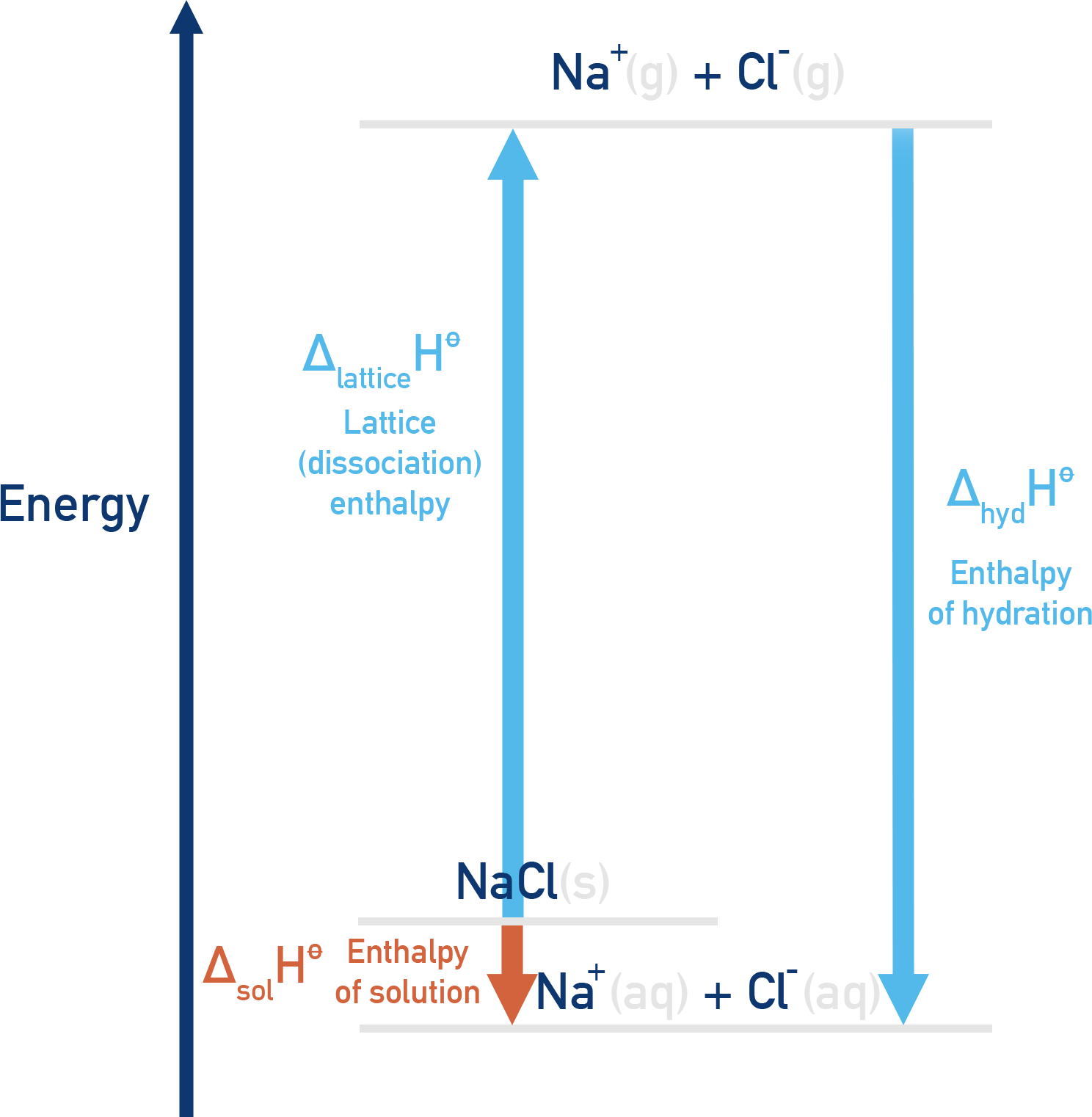
Example:NaCl
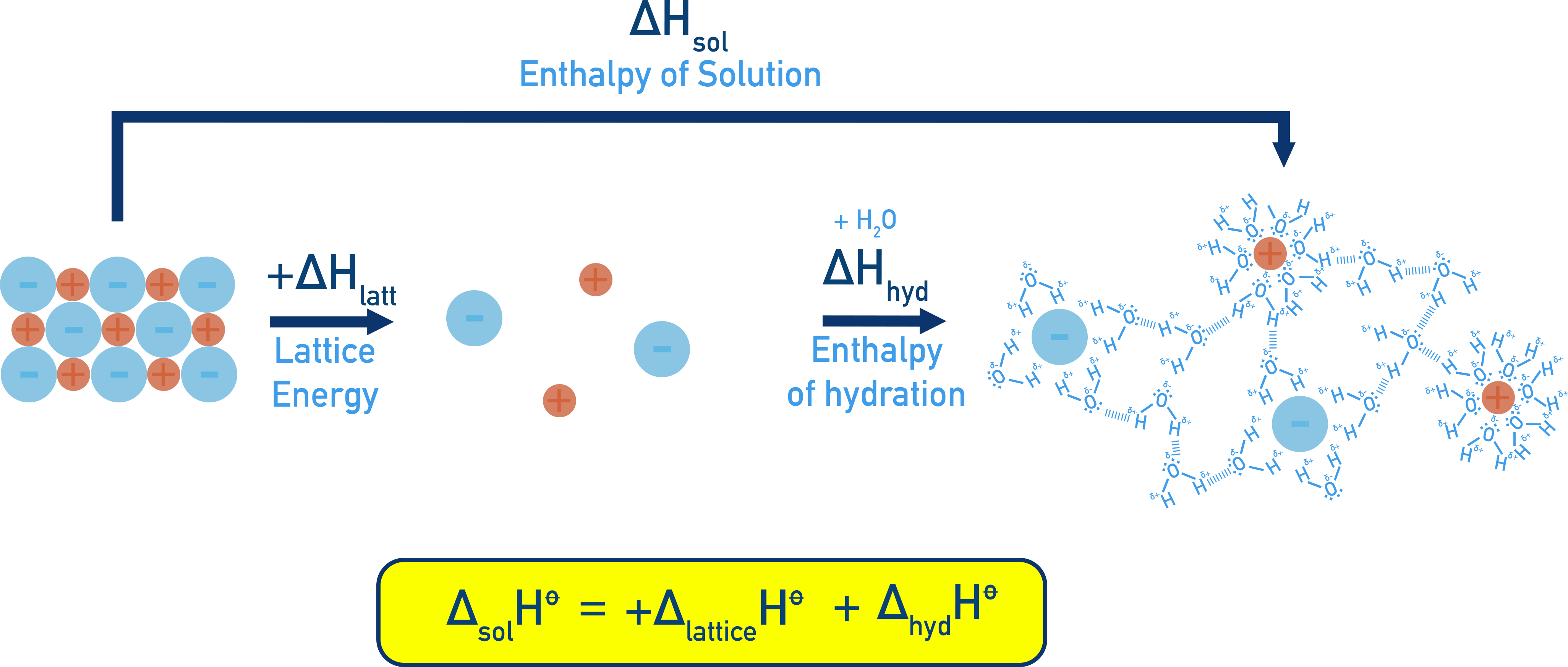
Where:
- ΔHlatt is positive (energy needed to break lattice)
- ΔHhyd is negative (energy released when ions are hydrated)
Enthalpy of Dilution
Enthalpy of dilution is the enthalpy change when more solvent is added to a solution, increasing the distance between solute particles and causing additional hydration.
As the solution becomes more dilute, hydration of ions continues and additional heat is released—though the amount of heat diminishes with each dilution.
NCERT Example: Dissolving HCl(g) in Increasing Amounts of Water
| Step | Reaction | ΔH (kJ mol−1) |
|---|---|---|
| S-0 | HCl(g) + 10 aq. → HCl·10 aq. | −69.01 |
| S-1 | HCl(g) + 25 aq. → HCl·25 aq. | −72.03 |
| S-2 | HCl(g) + 40 aq. → HCl·40 aq. | −72.79 |
| S-3 | HCl(g) + ∞ aq. → HCl·∞ aq. (infinite dilution) | −74.85 |
“aq.” denotes water used for hydration.
As more water is added, more hydration occurs and more heat is evolved.
However, the incremental change in ΔH becomes smaller with each step.
Eventually, the solution is infinitely dilute, and no more heat is released.
Summary
- Standard enthalpies describe heat changes for specific chemical and physical processes.
- Combustion is exothermic while atomisation and bond dissociation are endothermic.
- Bond enthalpies estimate reaction enthalpy using reactant minus product totals.
- Born–Haber cycles apply Hess’s Law to obtain lattice enthalpy indirectly.
- Solution and dilution enthalpies depend on the balance of lattice and hydration energies.
