The Ionic Product of Water, Kw
Quick Notes
- Water undergoes self-ionisation:
H2O (l) ⇌ H+ (aq) + OH− (aq) - The ionic product of water (Kw) is:

- At 298 K, Kw = 1.00 × 10−14 mol2 dm−6.
- For pure water at 298K:
- [H+] = [OH−] = 1.00 × 10−7 mol dm−3
- pH = 7.00 (neutral).
- pH of pure water changes with temperature, even though it remains neutral (because [H+] = [OH−]).
- Can use Kw to find the pH of an alkaline solution. Where:

Full Notes
The Ionic Product of Water, Kw has been covered in more detail
here.
This page is just what you need to know for AQA A-level Chemistry :)
Definition of Kw (The Ionic Product of Water)
In water, a very small percentage of molecules ionise, releasing H+ and OH− ions into solution.
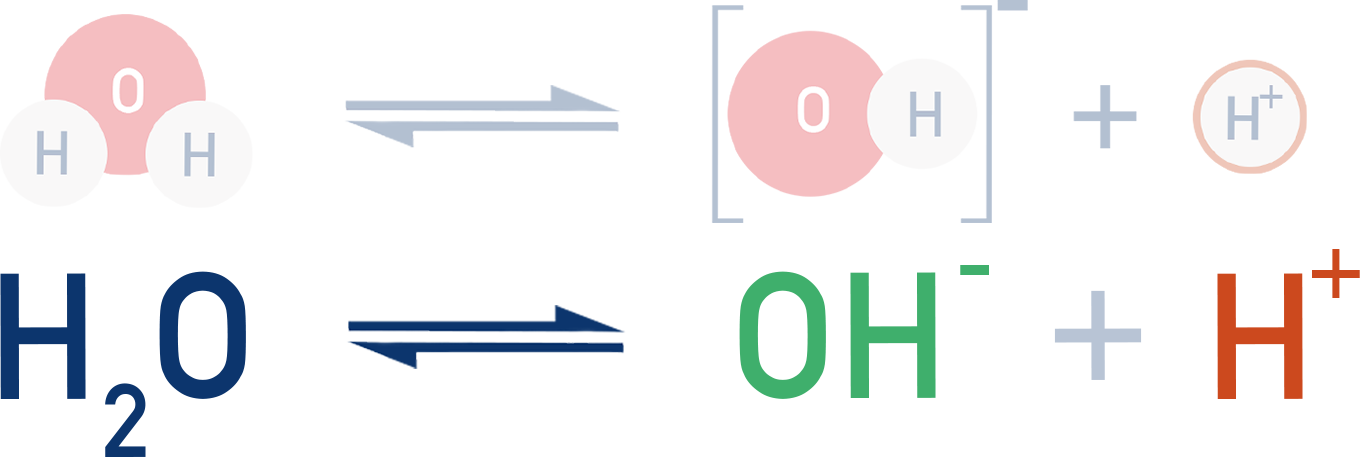
This is a reversible process and an equilibrium is established.
The equilibrium constant for this reaction is called Kw:

- At 298 K: Kw = 1.00 × 10−14 mol2 dm−6
- Kw changes with temperature
- Pure water is neutral when [H+] = [OH−]
Calculating pH from Kw
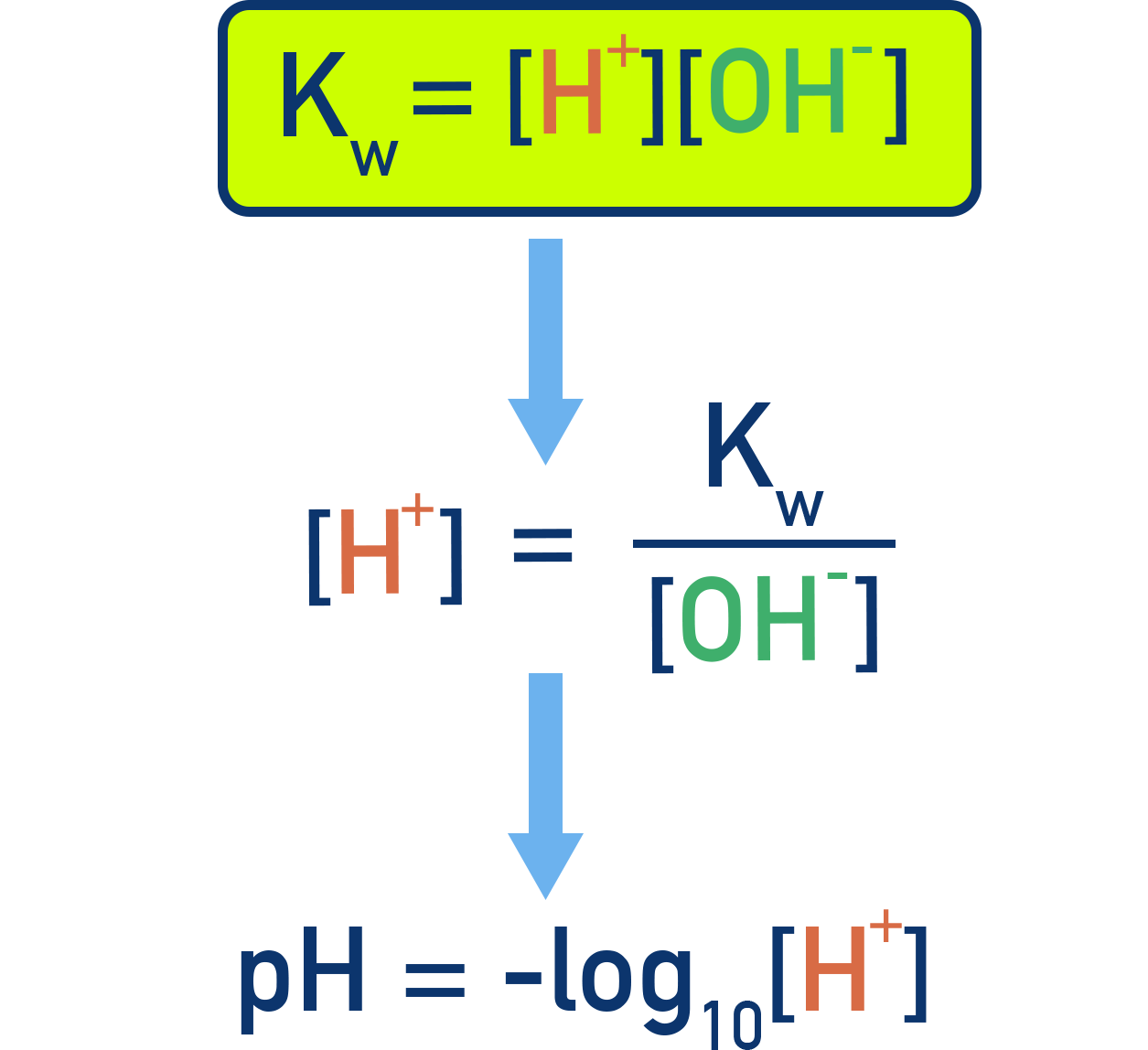
Kw can be used to find the pH of a pure (neutral) water or an alkaline solution (see below).
Since we know Kw = [H+][OH−] and pure water is neutral (that is [H+] = [OH−] then:
Kw = [H+]2
[H+] = √Kw
Find the pH of pure water at 298K given that Kw is 1.00 × 10−14 mol2 dm−6
- Kw = 1.00 × 10−14 mol2 dm−6
- [H+] = √(1.00 × 10−14)
- [H+] = 1.00 × 10−7 mol dm−3
- pH = -log(1.00 × 10−7) = 7.00
Effect of Temperature on Kw and pH
The forward direction for the ionisation of H2O is endothermic (+∆H).
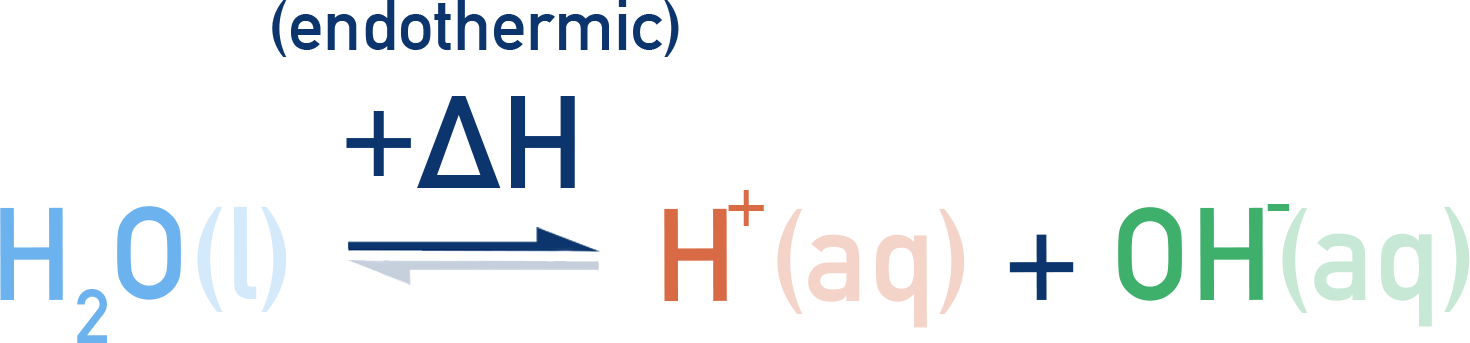
Meaning, when temperature is increased, equilibrium shifts to favour the forward direction - more ionisation occurs and [H+] and [OH−] increase. Kw increases with temperature.
Because the [H+] increases, the pH of the water decreases, however it is still neutral because [H+] = [OH−].
At 310 K, Kw = 2.45 × 10−14 mol2 dm−6. Calculate the pH of water at 310K.
- [H+] = √(2.45 × 10−14)
- [H+] = 1.56 × 10−7 mol dm−3
- pH = -log(1.56 × 10−7) = 6.81
Even though pH < 7, the solution is still neutral because [H+] = [OH−].
Kw in Acidic and Alkaline Solutions
In acidic solutions, [H+] > [OH−]
In alkaline solutions, [OH−] > [H+], but Kw
In both scenarios Kw remains constant (at a given temperature).
If a solution of sodium hydroxide has a concentration of 1.00 × 10−3 mol dm−3 at 298K, find the pH of the solution.
- [NaOH] = [OH−] = 1.00 × 10−3 mol dm−3
- Kw = [H+][OH−]
- [H+] = Kw / [OH−]
- [H+] = (1.00 × 10−14) / (1.00 × 10−3)
- [H+] = 1.00 × 10−11 mol dm−3
- pH = -log(1.00 × 10−11) = 11.00
Since pH > 7, the solution is alkaline.
Summary
| Concept | Key points |
|---|---|
| Self-ionisation of water | H2O (l) ⇌ H+ (aq) + OH− (aq) |
| Definition of Kw | Kw = [H+][OH−]; at 298 K, Kw = 1.00 × 10−14 mol2 dm−6 |
| Pure water (298 K) | [H+] = [OH−] = 1.00 × 10−7 mol dm−3; pH = 7.00 |
| Temperature effect | Ionisation is endothermic; increasing temperature increases Kw, increases [H+] and [OH−], lowers pH, but neutrality remains ([H+] = [OH−]). |
| Using Kw | For pure water: [H+] = √Kw. For alkaline solutions: [H+] = Kw ÷ [OH−]. |
- Kw links [H+] and [OH−] in water and depends on temperature.
- At 298 K, Kw = 1.00 × 10−14 mol2 dm−6; pure water has pH 7.00.
- We can use Kw to calculate pH for pure water and for alkaline solutions where [OH−] is known.
- As temperature increases, Kw increases and the pH of pure water decreases, but the water remains neutral.
