Weak Acids and Bases – Ka for Weak Acids
Quick Notes
- Weak acids partially dissociate in solution:
- Acid dissociation constant (Ka):
- pKa is related to Ka:
- Stronger weak acids have a larger Ka and smaller pKa.
- To calculate pH of a weak acid:
- Use Ka = ([H+]2) / [HA]
- Find [H+] = √(Ka × [HA])
- Use pH = -log[H+]

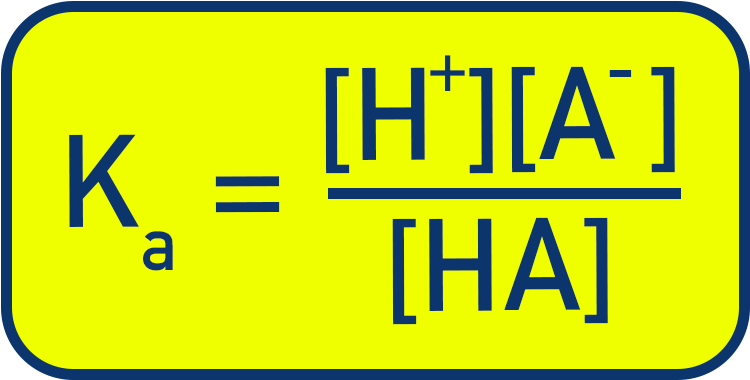
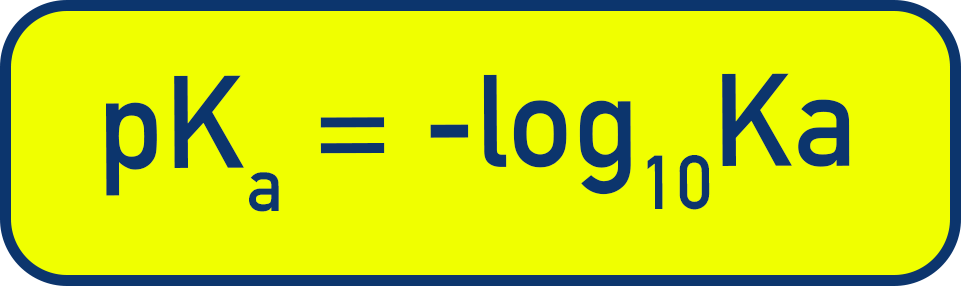
Full Notes
Ka has been covered in more detail
here.
This page is just what you need to know for AQA A-level Chemistry :)
Weak Acids and Their Partial Dissociation
A weak acid (HA) only partially dissociates in water:

Unlike strong acids (which fully dissociate), weak acids establish an equilibrium in solution between HA, H+ and A-.
The position of this equilibrium is based on the strength of the acid - the stronger the acid, the more the position lies to the right (more dissociation), meaning a higher concentration of H+ and A− ions in the mixture.
Example ethanoic acid (CH3COOH):
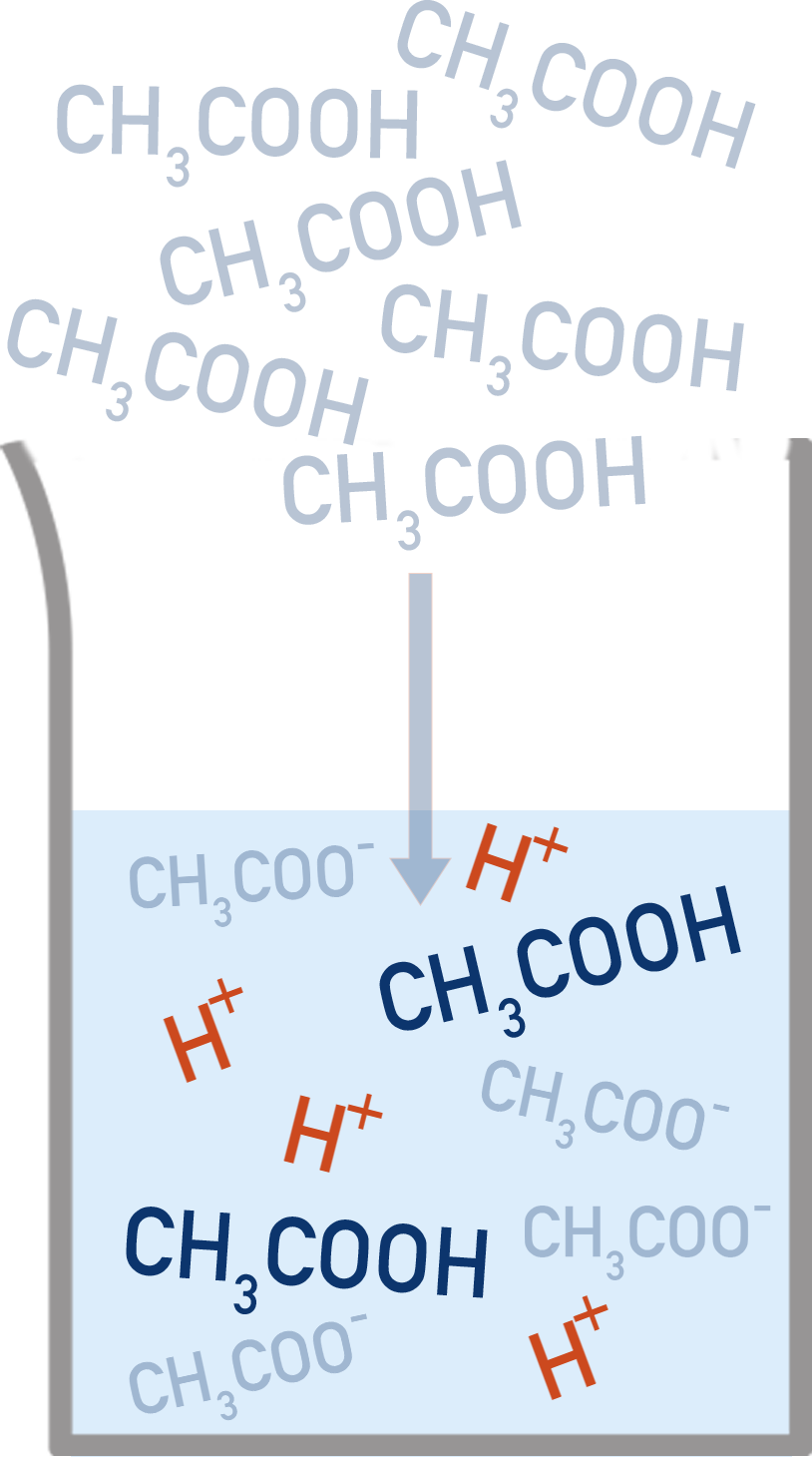
CH3COOH ⇌ H+ + CH3COO−
where HA = CH3COOH and A− = CH3COO−
Acid Dissociation Constant (Ka)
Like with any equilibrium system, the position of equilibrium for the dissociation of a weak acid can be described using an equilibrium constant.
Ka is the equilibrium constant for acid dissociation.
Expression for Ka:
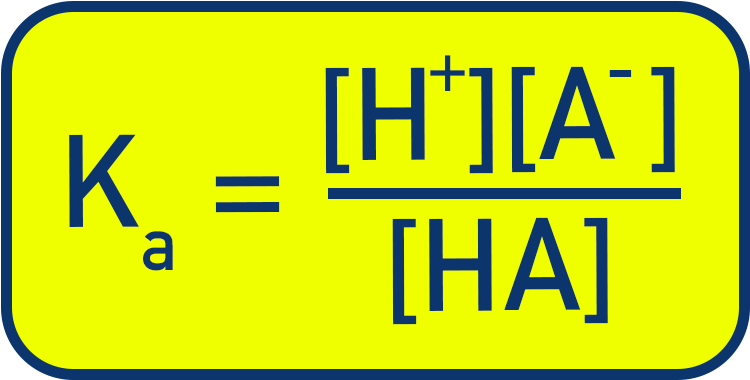
- Larger Ka = Stronger weak acid (more dissociation)
- Smaller Ka = Weaker acid (less dissociation)
Example For ethanoic acid (CH3COOH): CH3COOH ⇌ CH3COO− + H+
Ka = 1.75 × 10−5 mol dm−3 (shows weak dissociation).
Relationship Between Ka and pKa
pKa is a logarithmic measure of Ka:
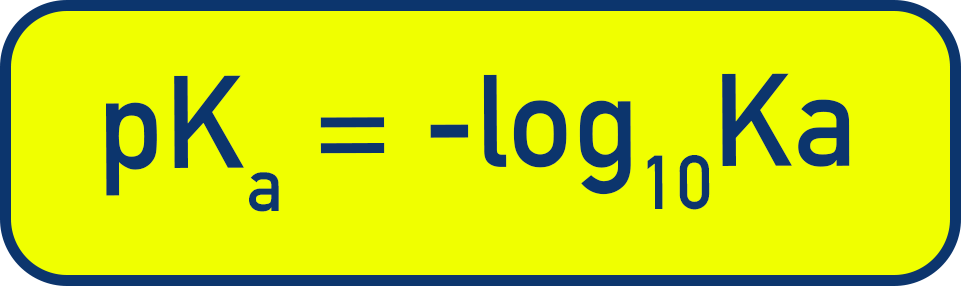
- Lower pKa = Stronger weak acid (more dissociation)
- Higher pKa = Weaker acid (less dissociation)
To convert pKa to Ka, use Ka = 10−pKa

Example
Ethanoic acid: Ka = 1.75 × 10−5, so pKa = 4.76.
Carbonic acid: Ka = 4.3 × 10−7, so pKa = 6.37.
Since pKa of ethanoic acid is lower, it is stronger than carbonic acid.
Calculating pH of a Weak Acid
Since weak acids partially dissociate with H+ and A− in a 1:1 ratio, we assume:
- [H+] ≈ [A−] (from dissociation).
- [HA] remains nearly unchanged.
This means we can assume that [H+] × [A−] = [H+]2
![AQA A-Level Chemistry relation showing Ka used to calculate [H+] for a weak acid](images/kaph.png)
Steps to Calculate pH of a Weak Acid:
![AQA A-Level Chemistry step-by-step flow to obtain pH from Ka and initial [HA]](images/h+toph.png)
- Use Ka expression: Ka = ([H+]2) / [HA]
- Rearrange to find [H+]: [H+] = √(Ka × [HA])
- Find pH: pH = -log[H+]

Don’t forget that when using Ka to find the pH of a weak acid, we are assuming two things - that [H+] = [A-] and that the [HA] at the start is the same as the [HA] at equilibrium. These are assumptions - for example the [HA] at equilibrium won’t be exactly the same as the initial [HA] as some will have dissociated however the amount of dissociation is very small compared to the concentration meaning mathematically it isn’t significant enough for us to worry about.
Find the pH of 0.10 mol dm−3 ethanoic acid (Ka = 1.75 × 10−5).
- [H+] = √(Ka × [HA])
- [H+] = √(1.75 × 10−5 × 0.10)
- [H+] = 1.32 × 10−3 mol dm−3
- pH = -log(1.32 × 10−3)
- pH = 2.88
Summary
| Concept | Explanation |
|---|---|
| Ka Definition | Ka = ([H+][A−]) / [HA] |
| pKa Calculation | pKa = -log(Ka) |
| Stronger Weak Acids | Large Ka, Small pKa |
| Weaker Weak Acids | Small Ka, Large pKa |
| pH of Weak Acid | Use [H+] = √(Ka × [HA]), then pH = -log[H+] |
- Weak acids partially dissociate; their strength is quantified by Ka and pKa.
- Larger Ka (smaller pKa) means a stronger weak acid; smaller Ka (larger pKa) means a weaker acid.
- For a weak acid HA, assuming [H+] ≈ [A−] and [HA] ≈ initial, use [H+] = √(Ka × [HA]) and pH = -log[H+].
