Rate Equations and the Arrhenius Equation
Quick Notes
- Rate equations describe how a reactions rate depends on reactant concentrations.
- General form of the rate equation:

k = Rate constant (varies with temperature)
[A], [B] = Reactant concentrations (mol dm−3)
m, n = Orders of reaction (must be determined experimentally) - Overall order of reaction = sum of individual orders (m + n).
- The rate constant (k) changes with temperature, following the Arrhenius equation:

where:
A = Arrhenius constant (pre‑exponential factor)
Ea = Activation energy (J mol−1)
R = Gas constant (8.31 J mol−1 K−1)
T = Temperature (K) - The equation can be rearranged into a linear form:
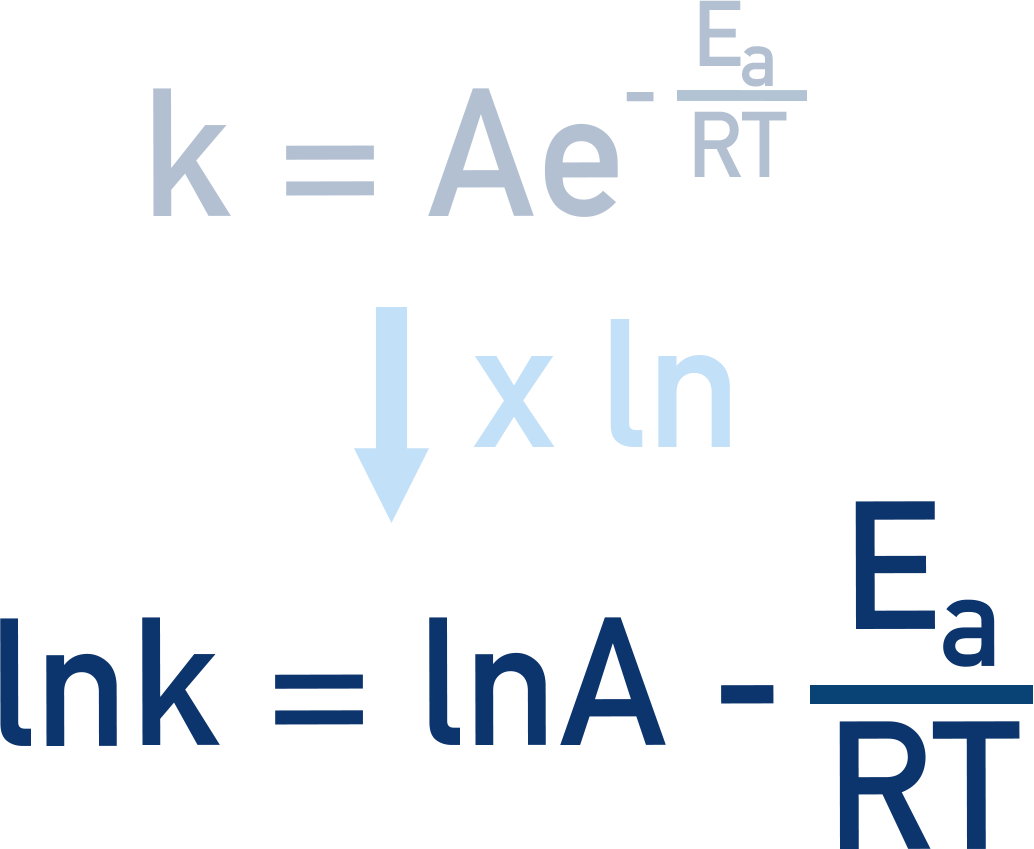
This allows us to find activation energy (Ea) and A by plotting a ln k vs. 1/T graph, with slope = −Ea/R.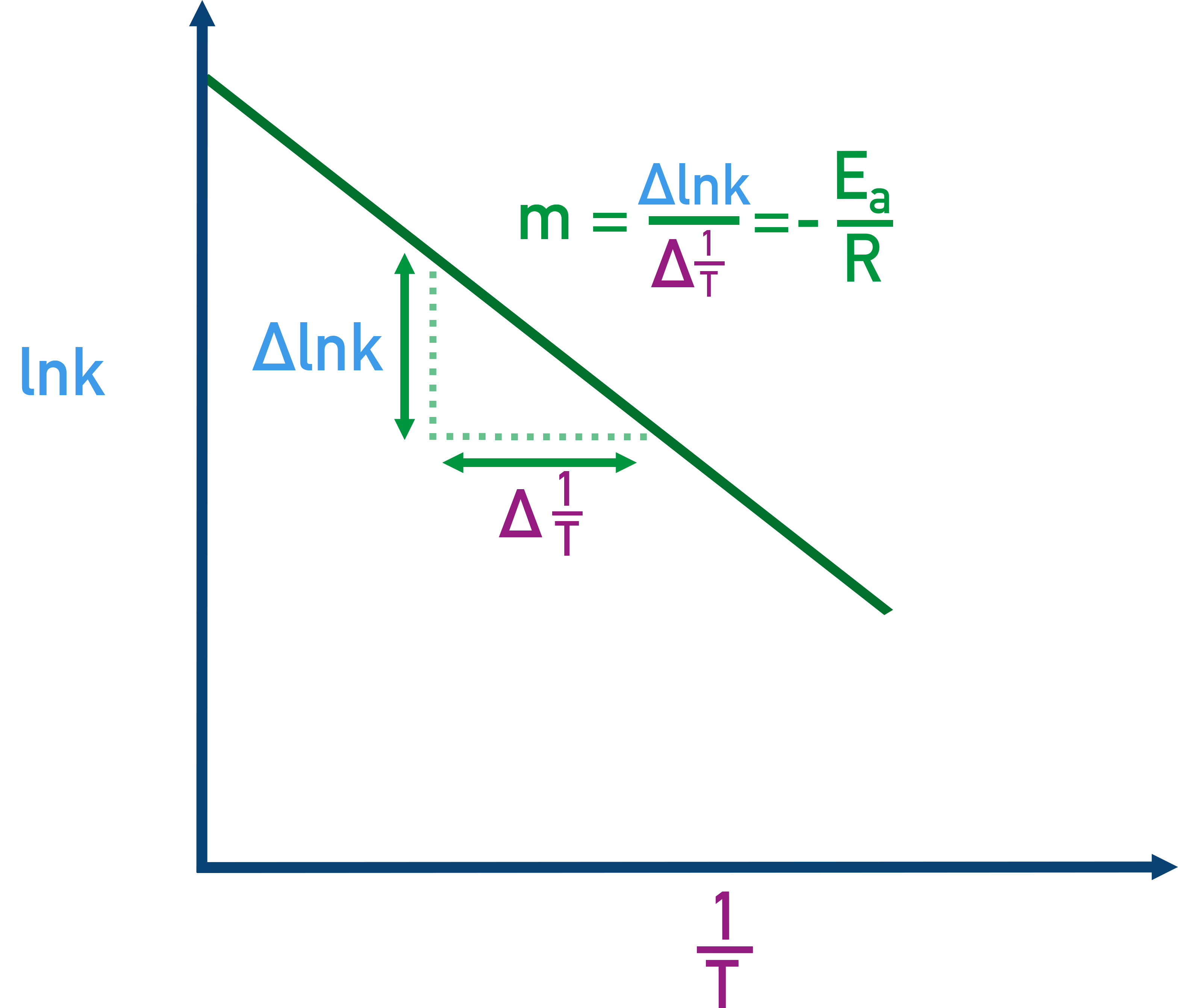
Full Notes
Rate Equation and Definitions
The rate of a reaction is a measure of how fast a reaction is occurring.

Rate equations shows how the rate of a reaction depends on reactant concentrations and the rate constant (k). where
- k = rate constant
- […] = concentration of reactant
- ^m and ^n = orders of reaction with respect to each reactant
Order of reaction:
Orders of a reaction link changes in concentrations of reactants to changes in the rate of a reaction. The order of a reaction ‘with respect to…’ just means how changing the concentration of a particular reactant affects the rate of the reaction (independent of other reactants).
There are three types of orders you need to know for A‑level Chemistry – zero order, first order and second order. Graph shapes and determining orders are covered here.
- zero order – changing the concentration of the reactant doesn’t affect the rate.
- first order – changing the concentration of the reactant changes the rate by the same factor (for example, if reactant concentration is doubled (×2), rate also doubles (×2)).
- second order – changing the concentration of the reactant changes the rate by the same factor squared (for example, if the reactant concentration is doubled, rate quadruples (22 = 4)).
Orders of reactions can only be determined experimentally and the overall order of a reaction is the sum of all orders for each reactant.
For Example:
For the reaction
A + B → Products
the rate equation is:
Rate = k [A]1 [B]2
Order with respect to A = 1 (First Order).
Order with respect to B = 2 (Second Order).
Overall order = 1 + 2 = 3 (Third Order).
Rate constant (k):
Temperature, activation energy and the proportion of collisions with correct orientation also determine a reactions rate. These are accounted for in a rate equation by the rate constant ‘k’.
k varies with temperature.
Rate Equation Calculations
Rate constants can be calculated using experimental data and a given rate equation. The units of k can vary for different reactions and depend on the overall order of reaction.
A reaction with the following rate equation and reactant concentrations has a reaction rate of 0.05 mol dm−3 s−1. Calculate the rate constant, k, for the reaction and give its units.
- Rate = 0.05 mol dm−3 s−1
- [A] = 0.10 mol dm−3
- [B] = 0.20 mol dm−3
- Rate equation: Rate = k [A]1 [B]2
Solve for k:
k = Rate ÷ ([A]1 [B]2)
k = (0.05) ÷ (0.10 × 0.202)
k = 0.05 ÷ (0.10 × 0.04)
k = 12.5 mol−2 dm6 s−1
Units of k depend on the overall order of reaction.
The Arrhenius Equation and Arrhenius Plots
The Arrhenius Equation, how to rearrange it and using Arrhenius Plots has been covered in much more detail here. What is on this page is just the essentials you need to know for AQA A‑level chemistry.
The Arrhenius equation shows how activation energy (Ea), temperature (T) and the proportion of collisions with correct orientation (A) can be linked together by the rate constant, k.

- A = Arrhenius constant (collision frequency factor).
- Ea = Activation energy (J mol−1).
- R = Gas constant (8.31 J mol−1 K−1).
- T = Temperature (K).
The equation shows why k increases with temperature – the e−Ea/RT part of the expression gets bigger as temperature (T) increases.
The Arrhenius equation is an exponential equation because it contains ‘e’. To make it easier to work with, we can rearrange it to a straight line form by multiplying both sides by ln:
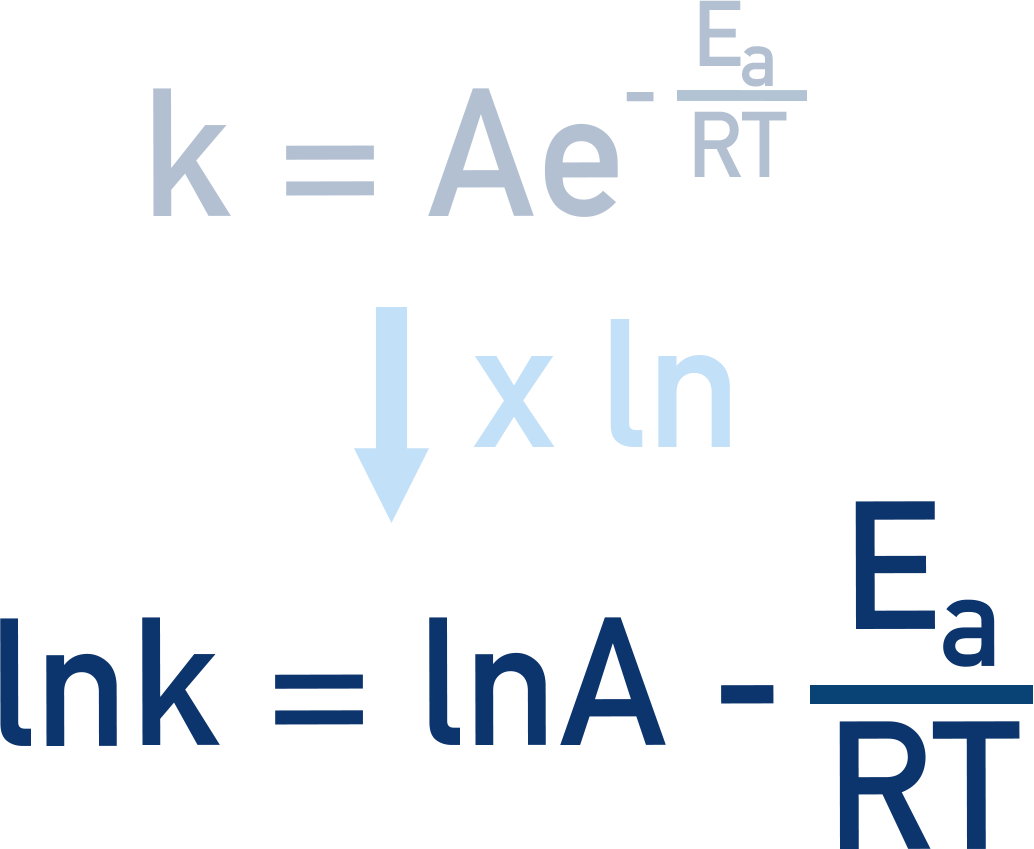
This can be rearranged a little to follow the y = mx + c function of a straight line. Where y = ln k and x = 1/T.
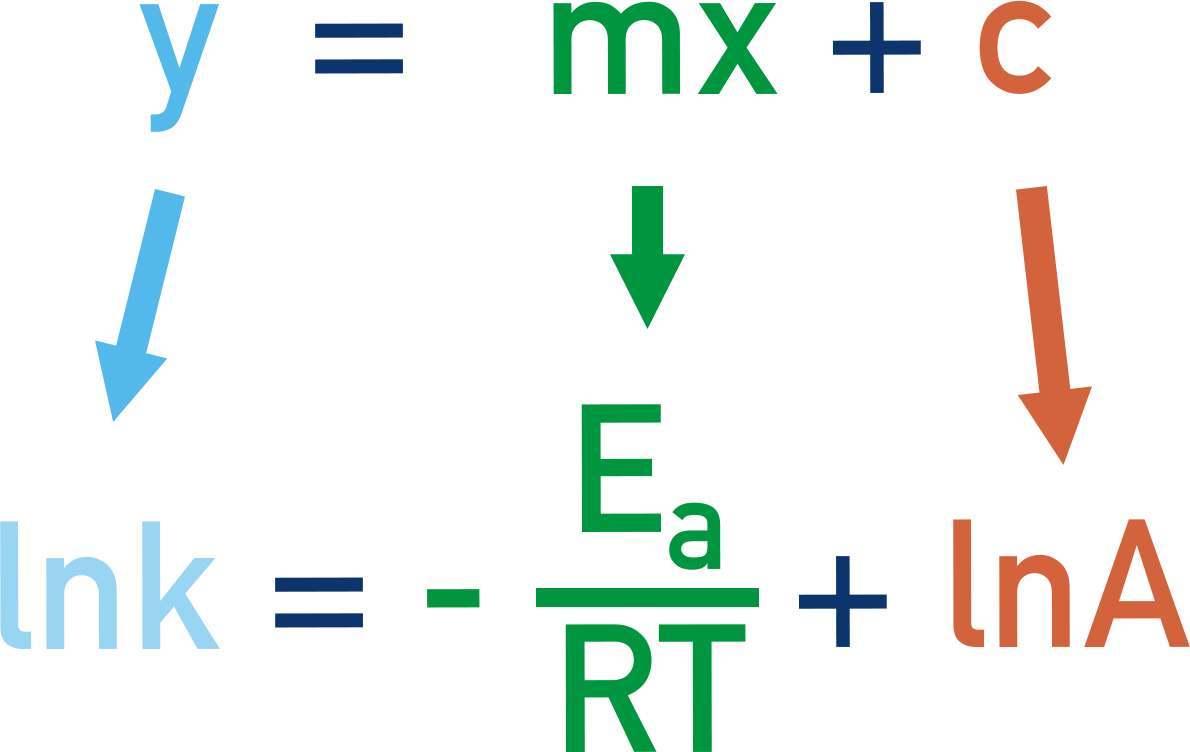
This allows us to plot ln k vs. 1/T (called an Arrhenius plot).

−Ea ÷ R = m → Ea = − m × R
Arrhenius Equation Calculations
A reaction has the following rate constants, k, at 300 K and 350 K. Determine the activation energy, Ea, for the reaction.
- At 300 K, k = 2.5 × 10−3 s−1
- At 350 K, k = 5.0 × 10−3 s−1
Use:
ln (k2 / k1) = (−Ea / R) × (1/T2 − 1/T1)
ln (5.0 × 10−3 / 2.5 × 10−3) = (−Ea / 8.31) × (1/350 − 1/300)
ln 2 = (−Ea / 8.31) × (−4.76 × 10−4)
Ea = (ln 2 × 8.31) / (4.76 × 10−4)
Ea = 12 110 J mol−1 = 12.1 kJ mol−1
Using an Arrhenius Graph to Find Activation Energy
The gradient of an Arrhenius plot is −Ea/R. By plotting ln k vs. 1/T, we can use the gradient of the straight line to find Ea.
Plot ln k vs. 1/T.
The gradient = −Ea / R.
Multiply the gradient by −8.31 to find Ea.

When using the Arrhenius equation in calculations, don’t forget units of activation energy (Ea) are kJ mol−1! The gas constant, R, has units of J K−1 mol−1, meaning you must convert any calculated Ea value to kJ (divide by 1000).
Summary
| Concept | Definition / Relationship | Notes |
|---|---|---|
| Rate equation | Rate = k [A]m[B]n | m, n determined experimentally |
| Order (with respect to a reactant) | Power to which its concentration is raised | Zero: no effect; First: factor-for-factor; Second: factor squared |
| Overall order | m + n | Determines the units of k |
| Rate constant, k | Proportionality constant in rate law | Depends on temperature; units vary with overall order |
| Arrhenius equation | k = A e−Ea/RT | k increases with T; linear form: ln k = ln A − (Ea/R)(1/T) |
| Arrhenius plot | ln k vs 1/T | Slope = −Ea/R; intercept = ln A |
