Determination of Rate Equation
Quick Notes
- The rate equation is determined experimentally (found using experimental data).
- General form:
Rate = k [A]m [B]n
where m and n (orders of reaction) must be found experimentally. - Methods to determine orders of reaction:
- Initial Rate Method – Measures how rate changes with concentration.
- Continuous Monitoring – Plots concentration vs. time to determine order graphically.
- If we know the orders with respect to each reactant, we may be able to predict how the reaction occurs via a proposed mechanism.
- Rate-determining step (RDS): The slowest step in a mechanism. Only reactants involved this step appear in the rate equation.
- Units of the rate constant (k) depend on the overall order of reaction.
Full Notes
Why the Rate Equation Must Be Determined Experimentally
The rate equation cannot be predicted from a balanced chemical equation. It must be determined experimentally, as some reactants may not affect rate.
For multi-step reactions, the rate equation only includes reactants involved in the slowest step in a mechanism (the rate-determining step, RDS).
Experimental Methods to Determine Orders of Reaction
1. Initial Rate Method
We can measure how the initial reaction rate of a reaction changes when reactant concentrations are varied:
- Carry out the reaction multiple times, varying one reactant concentration at a time.
- Measure the initial rate for each experiment.
- Compare how the rate changes to determine reaction order.
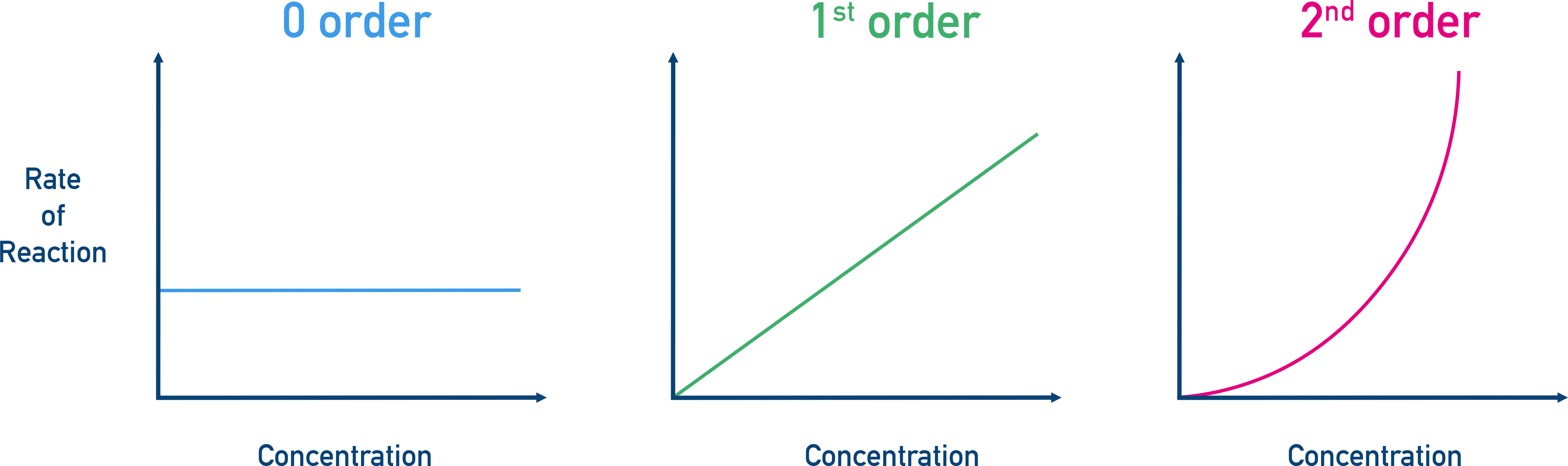
Graphs of rate vs. concentration can be used to identify order with respect to each reactant:
Find the rate equation for the following reaction using the given data.
Reaction: A + B → Products
| exp | [A] (mol dm⁻³) | [B] (mol dm⁻³) | Initial Rate (mol dm⁻³ s⁻¹) |
|---|---|---|---|
| 1 | 0.10 | 0.10 | 0.02 |
| 2 | 0.20 | 0.10 | 0.04 |
| 3 | 0.20 | 0.20 | 0.16 |
Workings:
- [A] doubled from exp. 1 to exp. 2, [B] constant → Rate doubled (0.02 → 0.04) → First order with respect to A.
- [B] doubled from exp. 2 to exp. 3, [A] constant → Rate ×4 (0.04 → 0.16) → Second order with respect to B.
- Rate equation: Rate = k [A]¹ [B]²
2. Continuous Monitoring Method
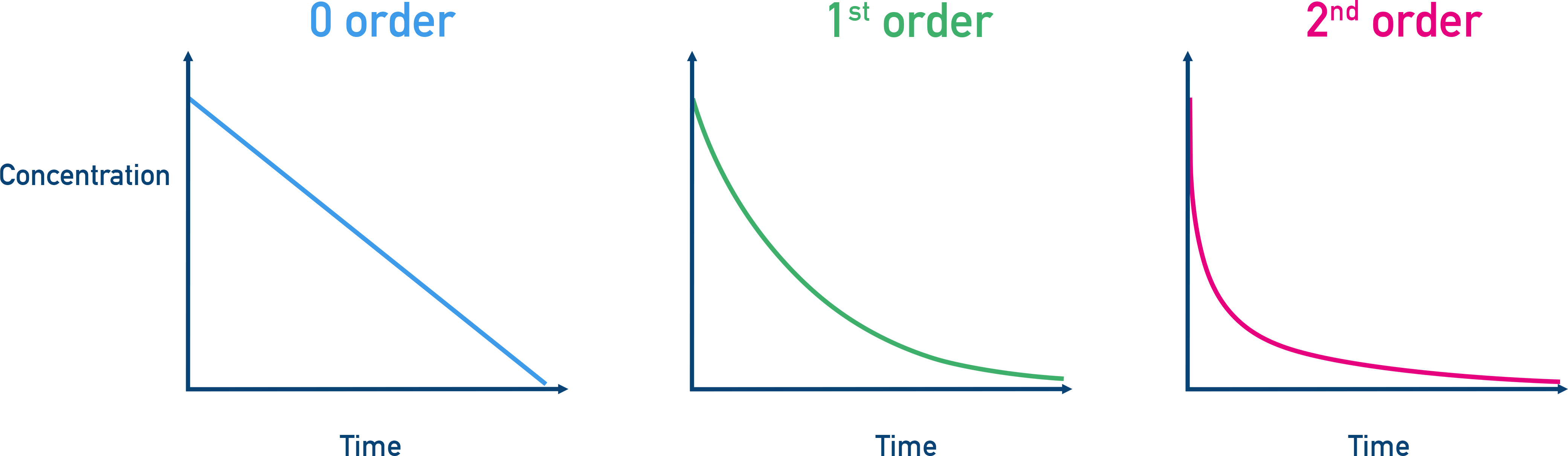
We can measure concentration at different times during a reaction. This is useful when it’s difficult to measure initial rates directly. Graphs of concentration vs. time are then used to determine the order.
Graphical Interpretation of Orders:
- Zero Order: Linear concentration vs. time graph.
- First Order: Exponential decay.
- Second Order: Steeper exponential decay.
Rate-Determining Step (RDS) and Reaction Mechanisms
Most reactions happen in multiple steps, with each step occuring at different rates.
The slowest step is the Rate-Determining Step (RDS). Only species involved the RDS appear in the rate equation.
Reaction: NO2 + CO → NO + CO2
The rate equation is Rate = k [NO2]2. Since CO does not appear in the rate equation, it is not involved in the rate-determining step (RDS).
Possible Mechanism:
- NO2 + NO2 → NO3 + NO (slow)
- NO3 + CO → NO2 + CO2 (fast)
Step 1 is the slow step (RDS), explaining why CO does not appear in the rate equation.

Remember that mechanisms are proposed using rate equations. They are only predictions — there may be more than one possible mechanism for a given rate equation.
Summary
- The rate equation cannot be predicted from the chemical equation — it must be found experimentally.
- Orders of reaction (m, n) are determined experimentally using the Initial Rate or Continuous Monitoring methods.
- Only species in the slowest step (RDS) appear in the rate equation.
- Worked examples and graphical methods are key tools to identify orders of reaction.
