The Ideal Gas Equation
Quick Notes
- The ideal gas equation: PV = nRT
- P = pressure (Pa)
- V = volume (m3)
- n = number of moles (mol)
- R = gas constant (8.314 J mol−1 K−1)
- T = temperature (K)
- Unit Conversions:
- Pressure: 1 atm = 101,325 Pa, 1 kPa = 1,000 Pa
- Volume: 1 dm3 = 0.001 m3, 1 cm3 = 0.000001 m3
- Temperature: T(K) = T(°C) + 273
- The equation assumes an ideal gas:
- Gas particles have negligible volume
- No intermolecular forces exist between molecules
- All collisions are elastic (no energy loss or gain)
- where:
Full Notes
More detailed background theory on the ideal gas equation and ideal gases has been covered here.
This page is just what you need to know for AQA A-level Chemistry :)
The behavior of gases can be described using the ideal gas law, which relates pressure, volume, temperature, and number of moles. Although no gas is truly ideal, most gases behave nearly ideally under many conditions.
What Is an Ideal Gas?
An ideal gas is a simplified model used in chemistry to help us understand and calculate gas behavior.
Real gases only approximate ideal behavior under normal conditions (room temperature and pressure), but the model itself is based on a set of assumptions.
These assumptions enable us to consider that only temperature, pressure and moles of a gas determine the volume occupied and we can ignore the type of gas it is.

Key Assumptions of the Ideal Gas Model
To behave as an ideal gas, a substance must meet these assumptions:
- The volume of individual gas particles is negligible
The size of the gas particles is so small that their total volume is effectively zero compared to the container. - No intermolecular forces exist
There are no attractions or repulsions between gas particles. They do not interact except during collisions. - All collisions are elastic
When gas particles collide, they do not lose kinetic energy. The total kinetic energy before and after a collision is the same. - Temperature is related to average kinetic energy
The higher the temperature, the faster the particles move.
All particles have different kinetic energies, but the average increases with temperature.
The Ideal Gas Equation
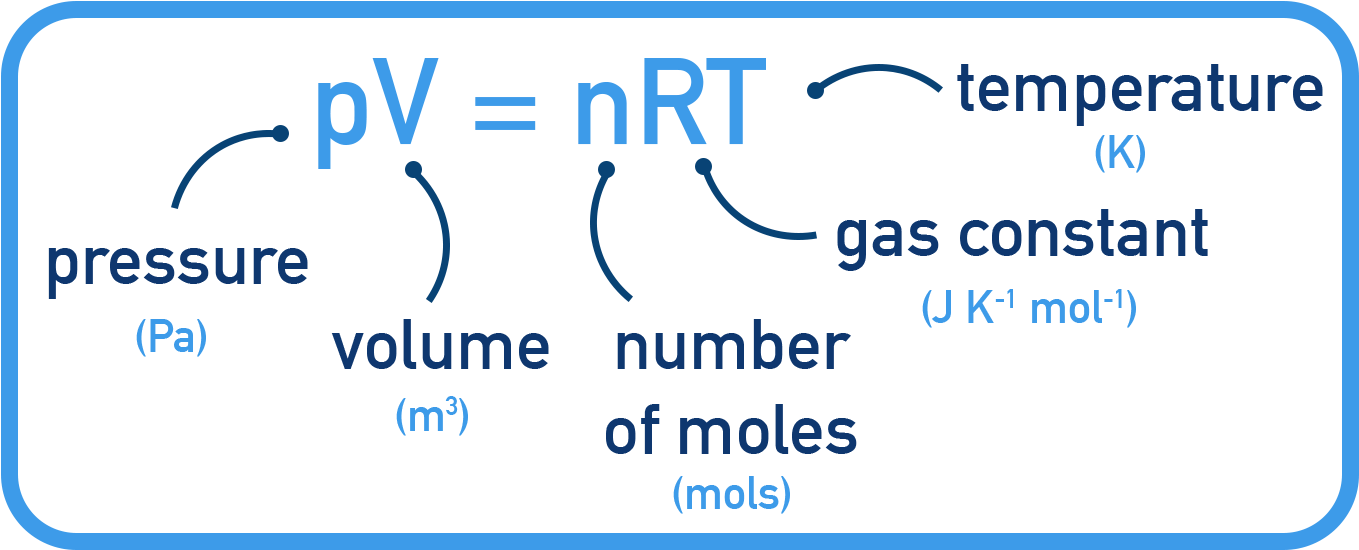
The ideal gas equation is:
PV = nRT
This relates pressure (P), volume (V), temperature (T), and moles (n) of a gas. The gas constant (R) has a value of 8.314 J mol−1 K−1.
Units Breakdown
| Symbol | Meaning | SI Unit |
|---|---|---|
| P | Pressure | Pascals (Pa) |
| V | Volume | Cubic meters (m3) |
| n | Moles of gas | moles (mol) |
| R | Gas constant | 8.314 J mol−1 K−1 |
| T | Temperature | Kelvin (K) |
Unit Conversions for the Ideal Gas Equation
- Pressure: 1 atm = 101,325 Pa; 1 kPa = 1,000 Pa
- Volume: 1 dm3 = 0.001 m3; 1 cm3 = 0.000001 m3
- Temperature: Always use Kelvin (K). Convert from Celsius: T(K) = T(°C) + 273.15

Always double check all units when using the ideal gas equation – pressure in Pa, temperature in K, and volume in m3. Convert before inserting values.
Using the Ideal Gas Equation
You can use PV = nRT to calculate any missing variable when the others are known.
Finding Volume: A gas sample has P = 100 kPa, n = 0.50 mol, and T = 298 K. What is its volume?
- Convert pressure to Pa: 100 kPa = 100,000 Pa
- Rearrange for V: V = (nRT) ÷ P
- Substitute: V = (0.50 × 8.314 × 298) ÷ 100000
- Answer: V = 0.0124 m3 = 12.4 dm3
Ideal vs. Real Gases
As stated above, the ideal gas law assumes:
- No particle volume
- No intermolecular forces
- Elastic collisions
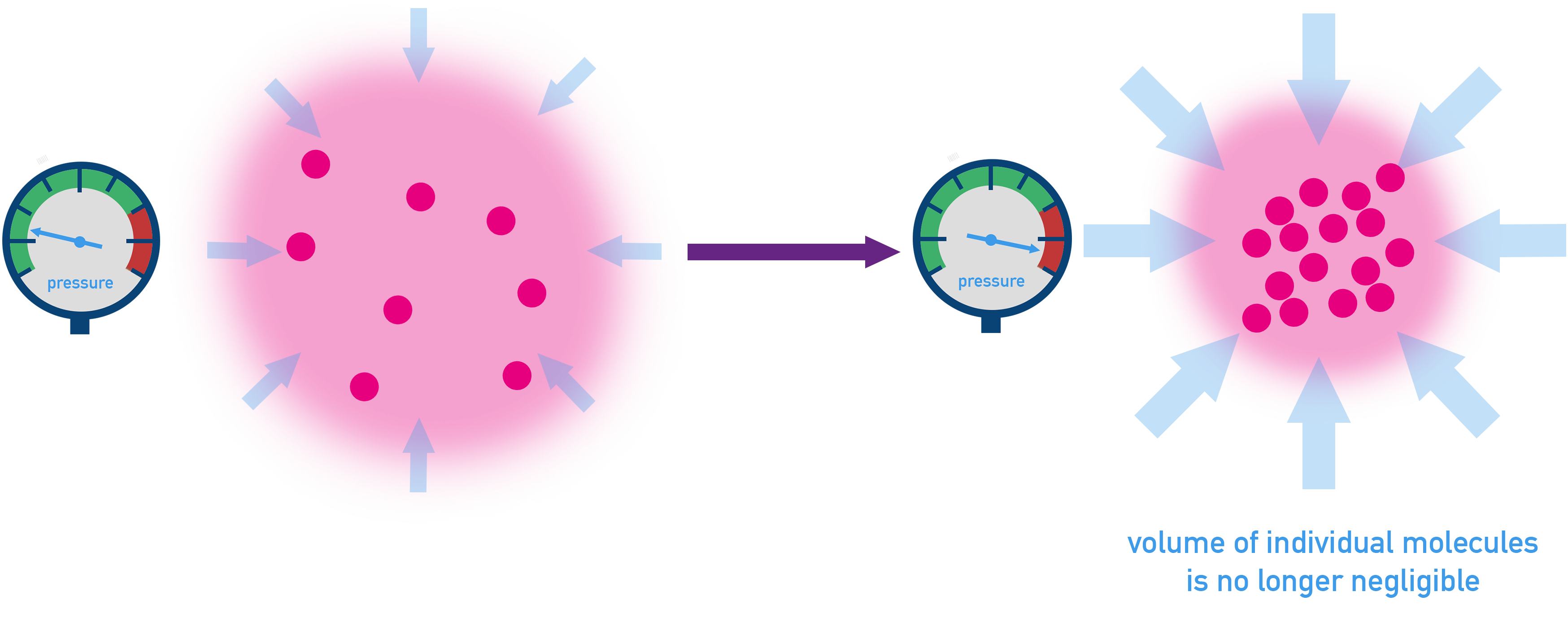
- At high pressures, gas particles occupy space, meaning their volume is no longer negligible.
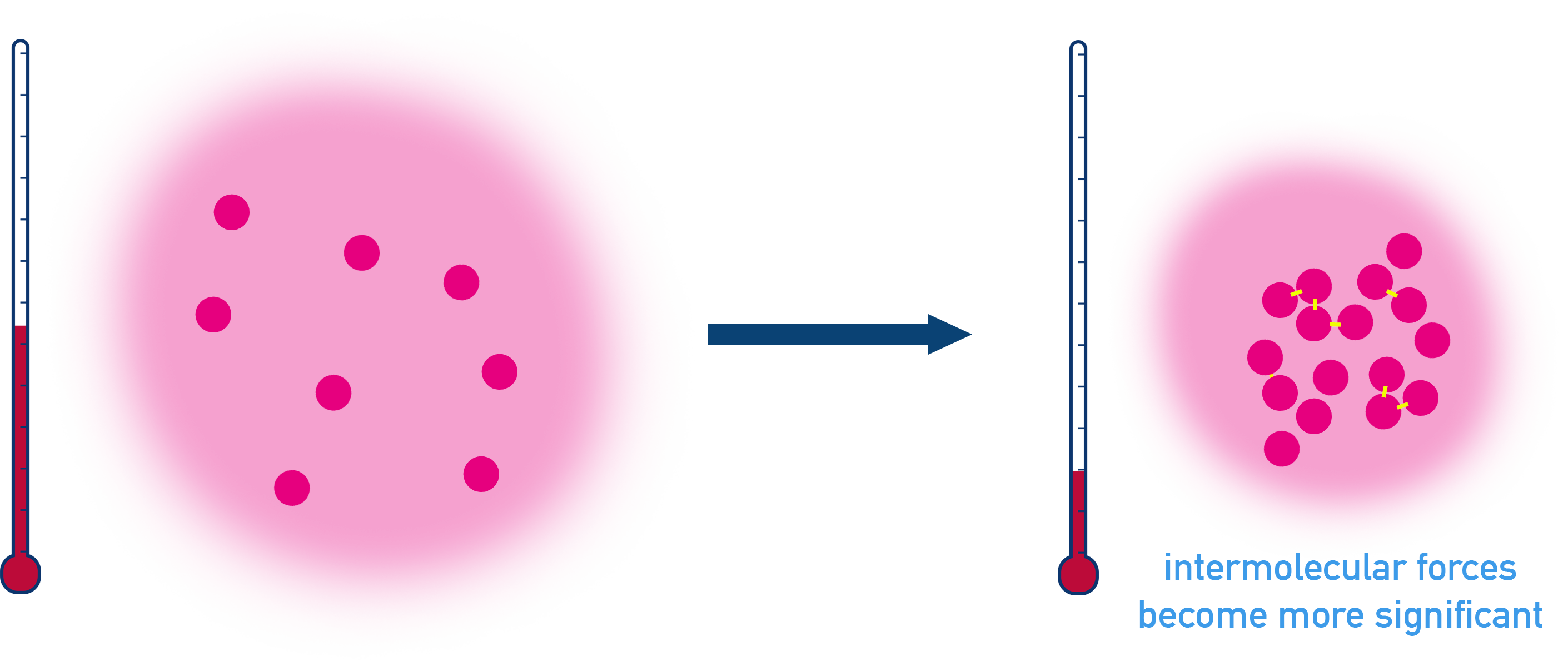
- At low temperatures, intermolecular forces become significant, making gases more likely to condense.
Summary
- The ideal gas equation is pV = nRT.
- Always use SI units: Pa, m3, K.
- Unit conversions are key (kPa → Pa, dm3 → m3, °C → K).
- Useful for calculating pressure, volume, moles, or temperature when others are known.
- Real gases deviate from ideal assumptions at high pressure and low temperature.
