Video Tutorial Arrhenius Equation
Quick Notes Arrhenius Equation
- Arrhenius equation is:

- Where:
- k = rate constant
- A = Arrhenius Constant (pre-exponentional factor)
- Ea= Activation Energy
- T = Temperature
- R = Gas Constant
- The equation can be rearranged by taking natural logs (ln) of all values:

- The larger the value of k, the faster the rate of a reaction
- The higher the activation energy, the smaller the value of k (slower rate of reaction)
- The higher the temperature, the greater the value of k (faster rate of reaction)
- Arrhenius constant (A) is based on the proportion of particles colliding with the correct orientation for a reaction to occur
Full Notes Arrhenius Equation
What is the Arrhenius Equation?
The Arrhenius equation shows the relationship between k (rate constant), activation energy, temperature and collisions of reactant particles (with correct orientation).
The equation is:

k = rate constant
A = Arrhenius constant (pre-exponential factor)
Ea = Activation Energy (kJmol -1)
T = Temperature (Kelvin, K)
R = Gas constant (kJ K-1 mol-1)
As the rate of a reaction is based on k (see rates of reaction), the rate constant gives an indication of the rate of a reaction (high value for k = fast rate of reaction; low value for k = slow rate of reaction).
There are two main parts to the Arrhenius equation:
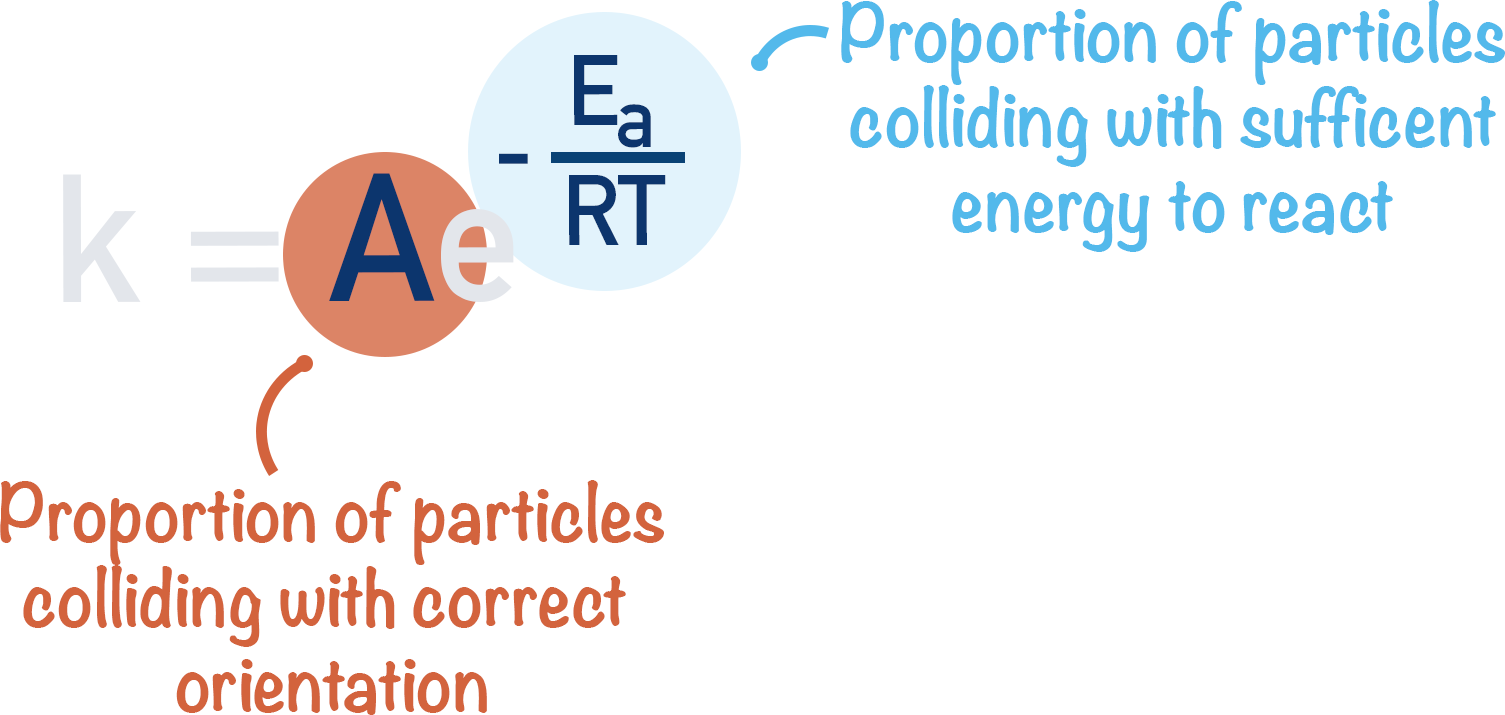
The Arrhenius Constant

A is the Arrhenius constant (sometimes called the ‘pre-exponential factor’) and refers to the proportion of molecules colliding with the ‘correct orientation’.
This is essentially the number of particles that would react if the activation energy was zero. Correct orientation refers to particles colliding in the ‘right way’ to react – like pushing a door – you not only have to push a door to open it, you have to push in the right direction! Reacting particles not only have to collide with each other, they have to hit each other in the right way to react.
e-Ea/RT

e-Ea/RT is the fraction of molecules that have the required activation energy to react. The bigger this value, the faster the reaction, as more particles have the required activation energy.
The rate constant describes the proportion of particles colliding with the correct orientation that have the required activation energy to react.
What is e and why is it important?
When temperature increases, the rate of a reaction increases. When temperature decreases, the rate of a reaction decreases. This is because more or less particles have the required activation energy.
However, the proportion of particles with the required activation energy doesn’t change by the same factor as the temperature!
If you double the temperature of a reaction, the number of particles with the required activation energy increases by much more than double. Equally, if you half the temperature, the number of particles with the required activation energy decreases by more than half. This means the rate of a reaction doesn’t increase in a linear way with temperature. The graph looks something like this:
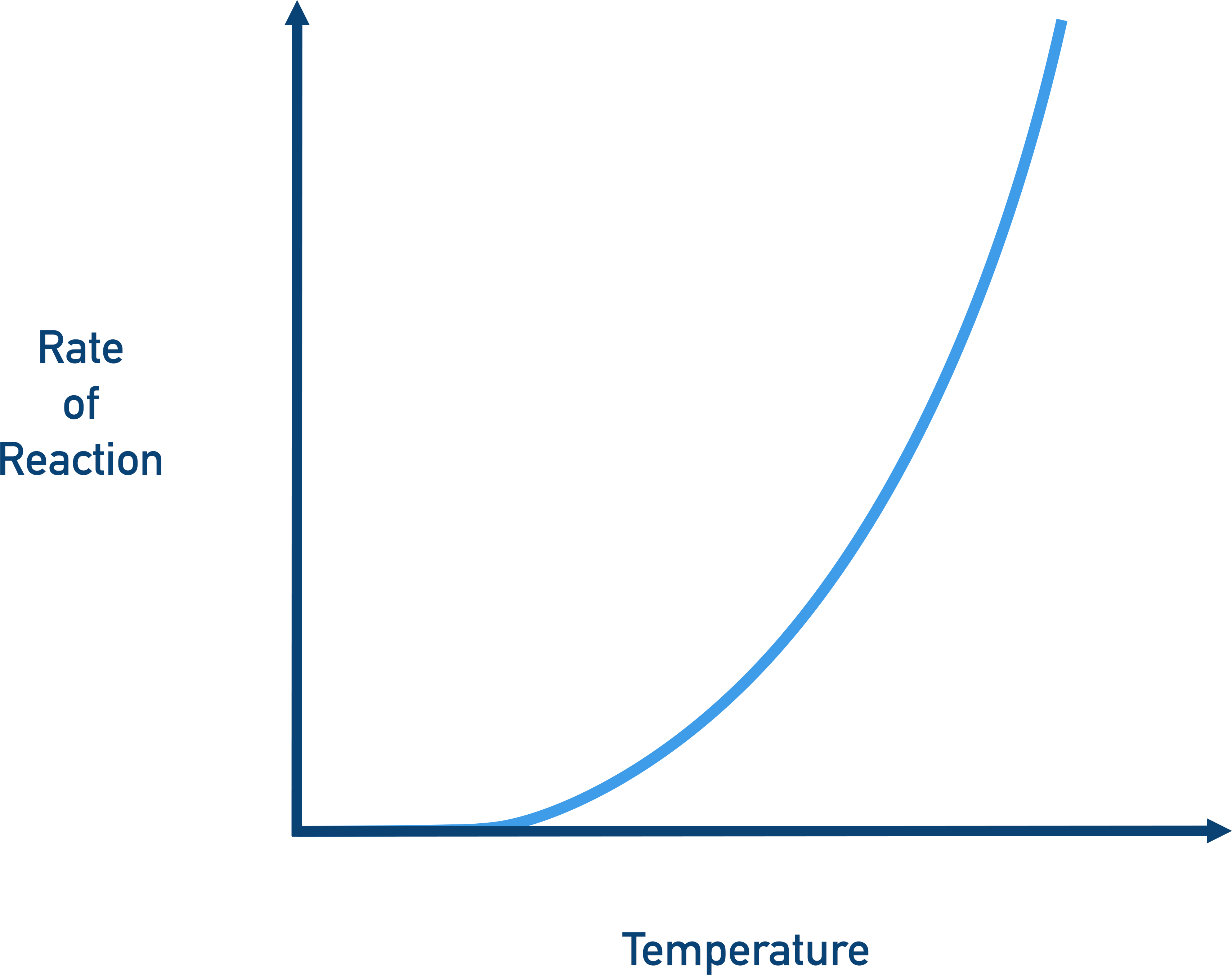
This kind of relationship is called exponential and the shape of the graph can be explained by a number ‘e’. For A-level chemists, there is nothing you need to know about this ‘e value’ other than it describes the shape of this curve. e is just a number (usually given as 2.718).
In more detail – the value of e (2.718…) describes the rate of change for an exponential (curved graph). The value of ex is the same as the gradient (dy/dx) at any point on the graph, meaning as x changes, the gradient of the line also changes – giving a curved line.
ln and Natural logs
To make things easier, we can remove e from the Arrhenius expression, by taking natural logs of both sides of the equation. Natural log is shown as ‘ln’ on your calculator. For more detail on how this works, see below – although you really don’t need to worry about it!
This converts the Arrhenius equation:
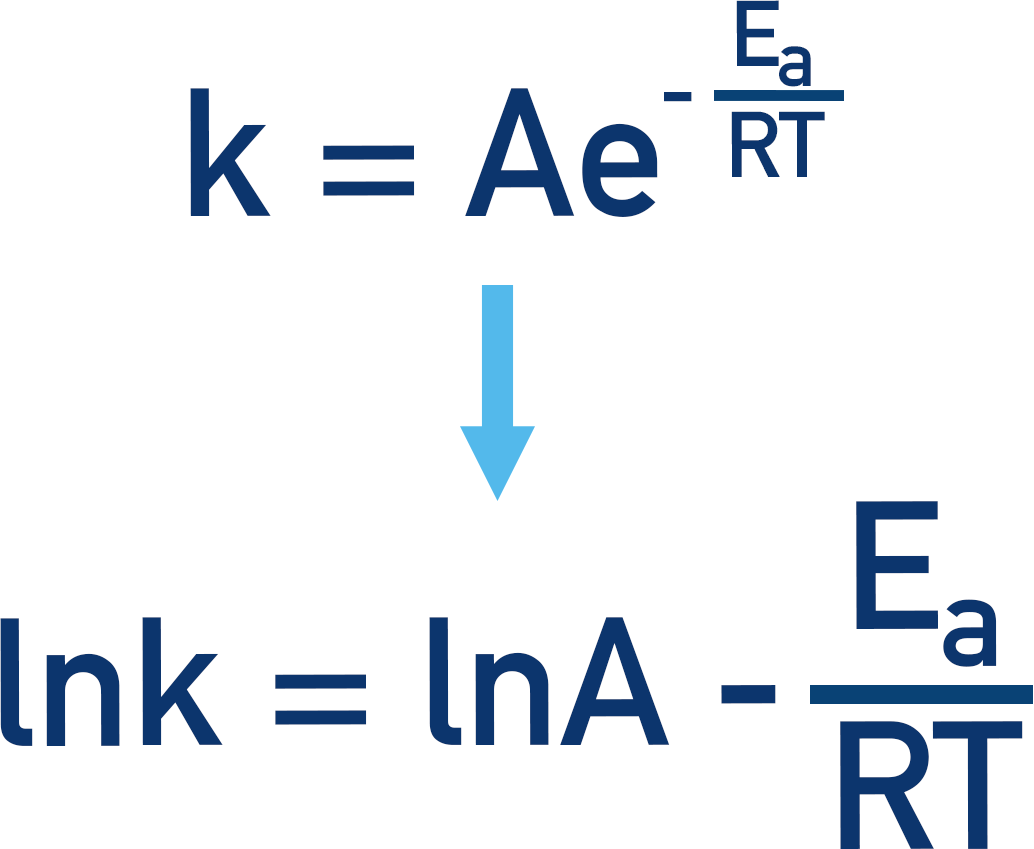
This makes things much easier as we now have a more ‘straightforward’ equation that we can rearrange to find an unknown value. The great thing is that we have ‘removed’ the exponential nature of the expression and a graphical plot of these values will give us a straight-line graph. This is very useful for finding activation energy and A (the Arrhenius constant). See Arrhenius Plots for how to do this.
How does temperature and activation energy affect rate constant, k?
If the activation energy for a reaction decreases (by using a catalyst, for example) then the rate of reaction will increase. If the temperature of a reaction increases, then the rate of the reaction will also increase.
In both of these cases, the proportion of particles with the required activation energy is increased, meaning that more collisions between particles lead to a reaction.
The proportion of particles with the required activation energy is shown in the Arrhenius equation as:

where Ea = activation energy and RT = gas constant x temperature
Note that R describes how much energy one mole of gas particles has per kelvin of temperature. By taking the temperature and multiplying it by the gas constant, we know how much available energy there is for one moles worth of particles.
The bigger the value of Ea, the bigger the value of Ea / RT (top of the fraction gets bigger, meaning a bigger value). This leads to a smaller value of e-Ea/RT.
For example, 2-1 = 0.5 whereas 2-2 = 0.25 and 2-4 = 0.06. The bigger the value of the negative power, the smaller the value created.
As k = A x e-Ea/RT, the bigger the value of e-Ea/RT, the smaller the rate constant. This is why as activation energy increases, the rate constant gets smaller (meaning the rate of reaction decreases).
If the temperature is increased, however, then the value of Ea/RT gets smaller (bottom of the fraction gets bigger, meaning a smaller value). This leads to a larger value of e-Ea/RT.
For example, 2-10 = 0.0009 whereas 2-5 = 0.03 and 2-1 = 0.5. The smaller the value of the negative power, the bigger the value created.
Again, as k = A x e-Ea/RT, the smaller the value of e-Ea/RT, the bigger the rate constant. This is why as temperature increases, the rate constant gets bigger (meaning the rate of reaction increases).
Why can k = Ae-Ea/RT be written as ln k = -Ea/RT + lnA?
This is a common question from students who aren’t studying mathematics at an advanced level. The truth is you don’t need to worry about WHY for A-level chemistry, but for those who are curious, this is outlined below.
A log just tells you how many times you have to multiply a number by itself to get to another value.
For example:
log2(8) = 3
This is because to get to the number 8, you have to multiply two by itself three times (2 x 2 x 2 = 8). This is the same as 23 = 8.
log2(2) must equal 1 as two multiplied by 1 = 2. If 2x = 2 then x must be 1.
This is why loge(e) = 1
as.. e only has to be multiplied by 1 to get = e. If ex = e, then x = 1.
Confused? I repeat - you really don’t need to know this for A-level chemistry!
A natural log (ln) refers to loge
e is just a number (2.71….), meaning that loge(e) = 1 (just like log2(2) = 1)
This means we can remove e from the Arrhenius expression by multiplying e by loge or ‘ln’. Remember – ln is just a number (log2.71…). Basic rules apply though and we must multiply everything in the expression by ln.
k= Ae-Ea/RT x ln
=
ln k = ln A ln e-Ea/RT
There is another rule that we need here!
We know that ln(ex) = loge(ex) (see above)
Remember a log is telling us how many times we need to multiply one number by to get to another value.
To go from e to ex, we need to multiply e ‘x’ number of times!
Meaning loge(ex) = x
This is really important for the Arrhenius equation as now, ln e-Ea/RT simply becomes –Ea/RT.
Meaning we can simplify the expression further.
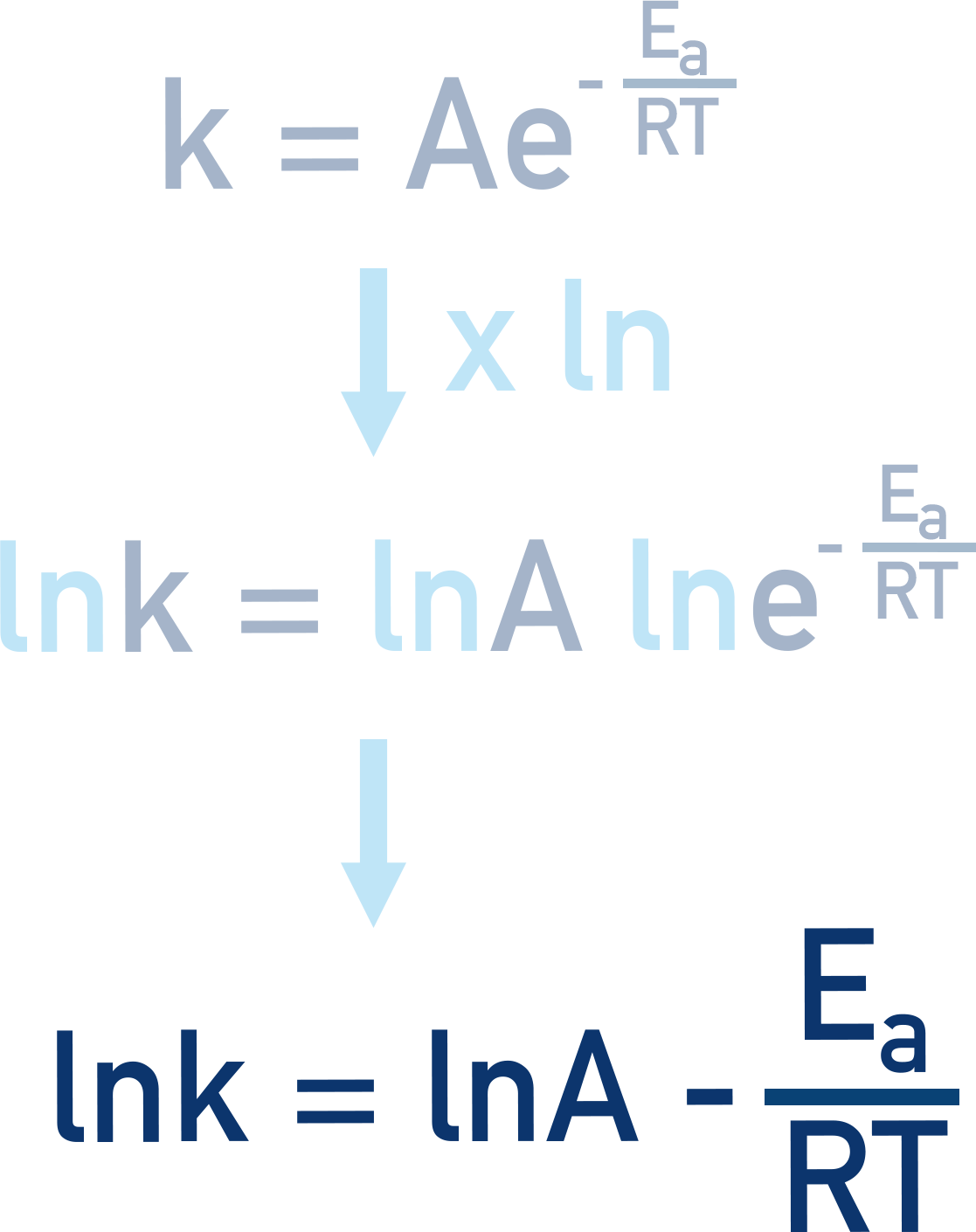
The great thing now is that we have ‘removed’ the exponential nature of the expression and a graphical plot of these values will give us a straight-line graph. This is very useful for finding activation energy and A (the Arrhenius constant). See Arrhenius Plots.
