Video Tutorial Arrhenius Plots
Quick Notes Arrhenius Plots
- The Arrhenius equation in the form y = mx + c can be used to find activation energy (Ea) and the Arrhenius constant, A.
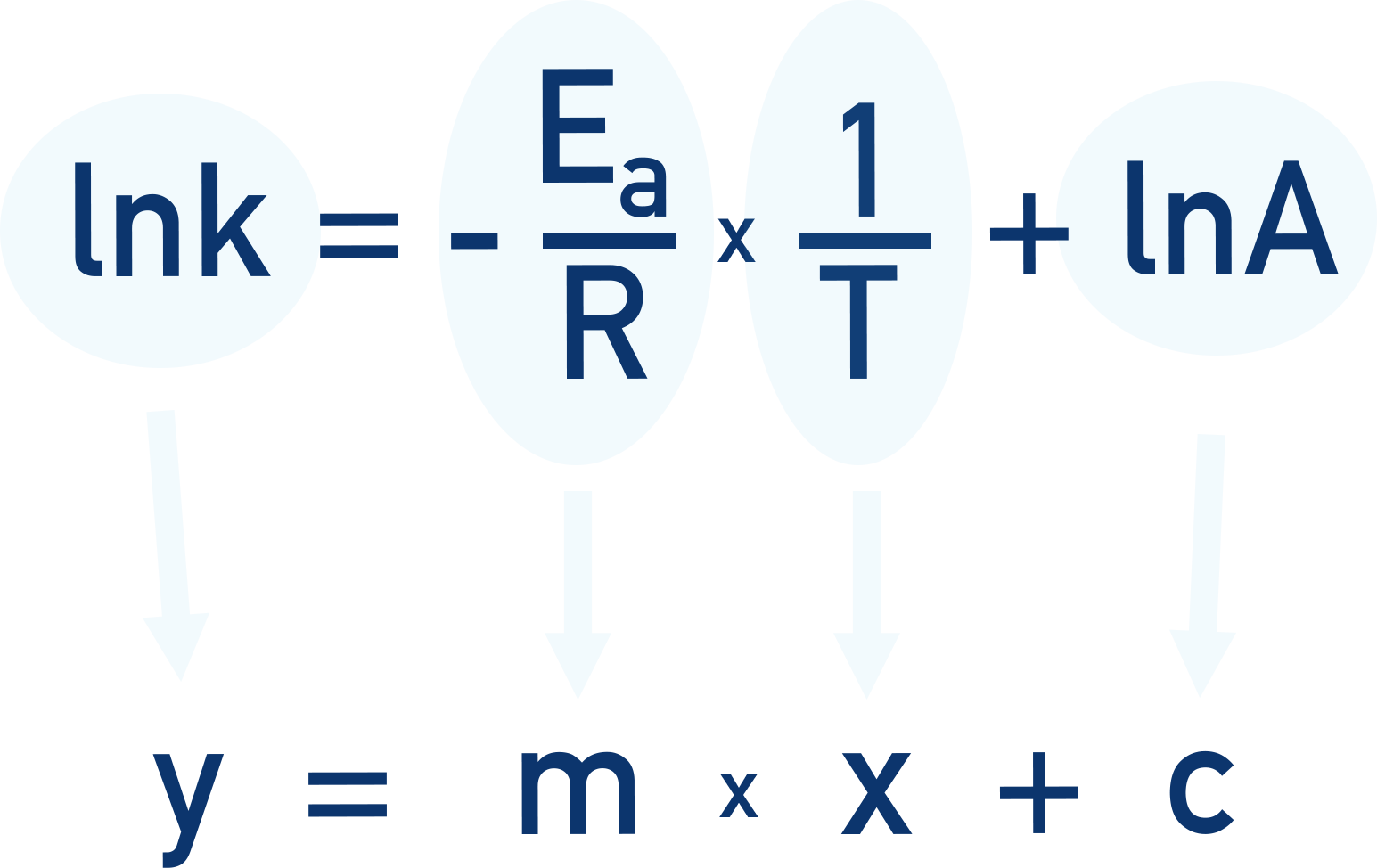
- To find activation energy (Ea) and A, plot a graph of lnk (as y axis) and 1/T (as x axis) and use the gradient, m to find activation energy.
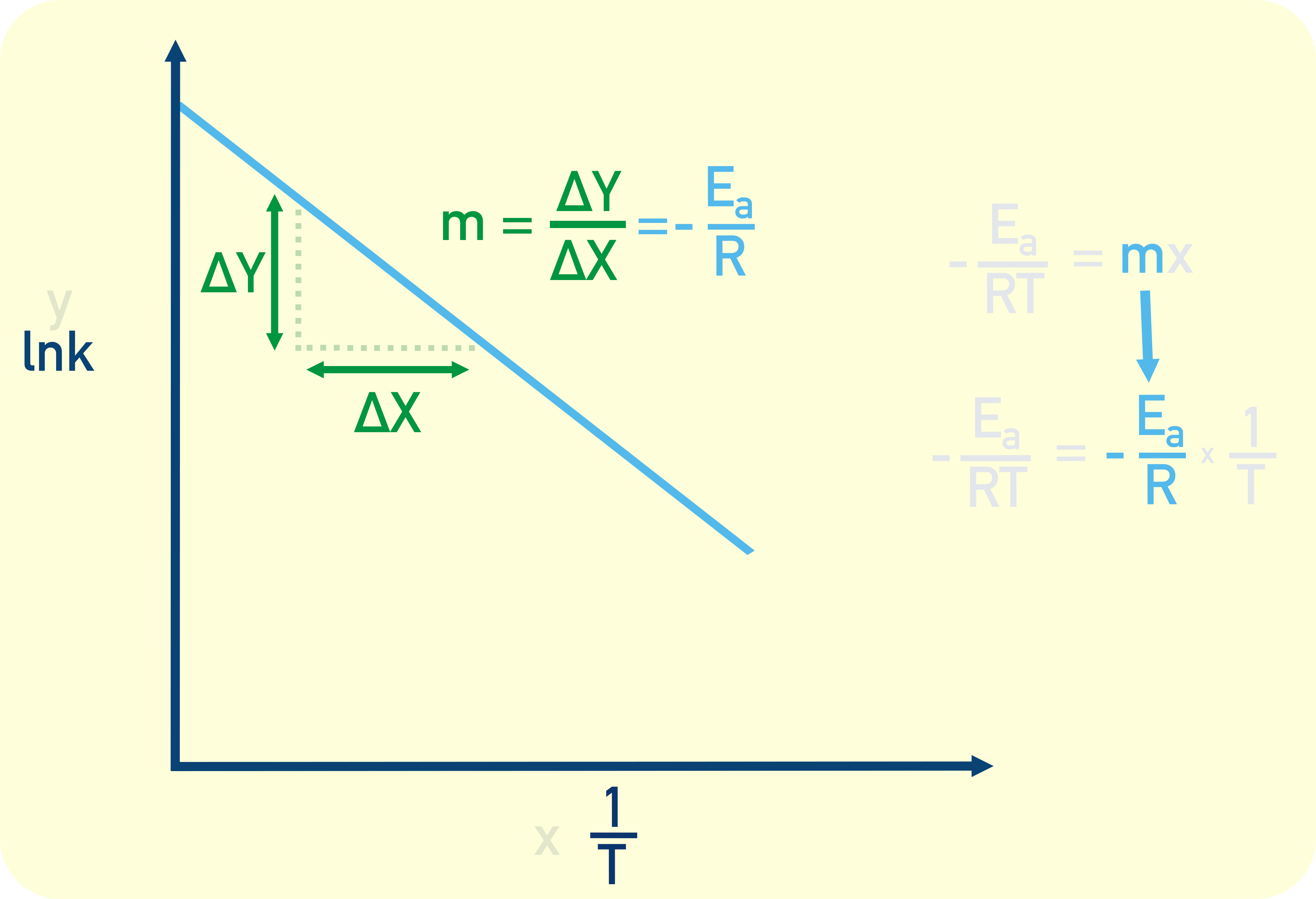
- Activation energy can then be found using the gradient:
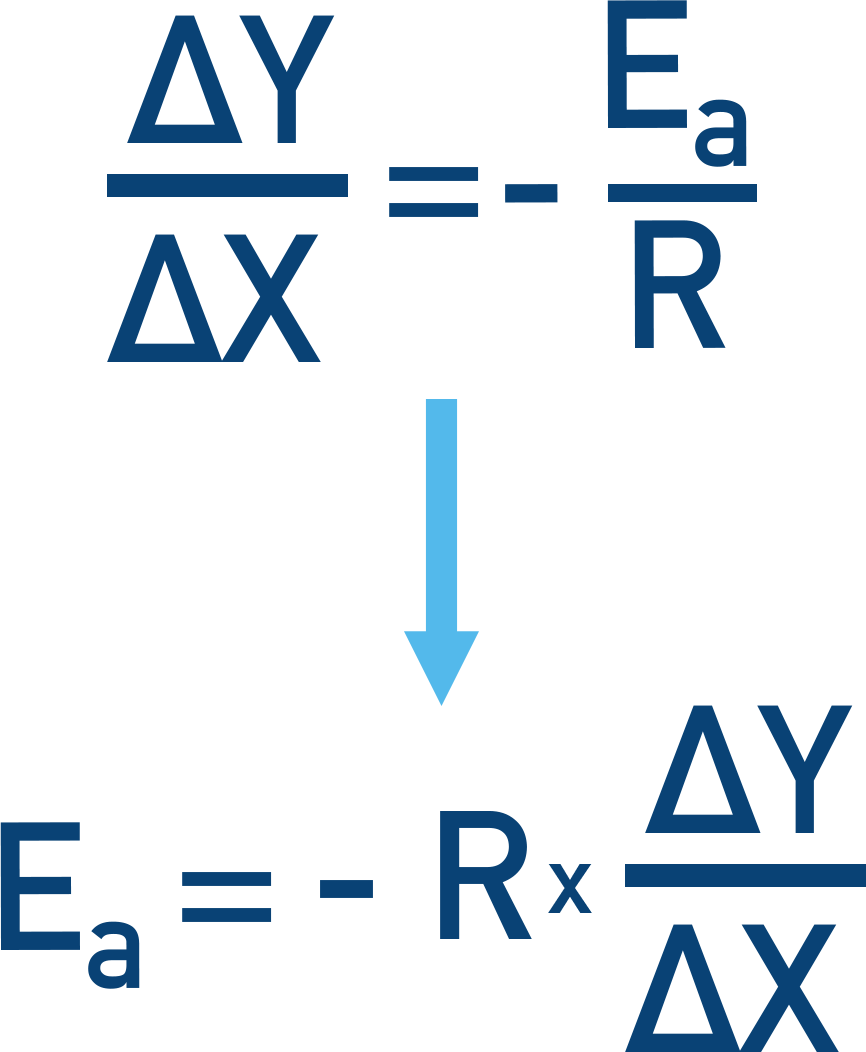
- The Arrhenius constant (A) is then found by substituting values into the original expression.

Full Notes Arrhenius Plots
Recall that the Arrhenius equation can be re-written by taking natural logs of all values in the expression:
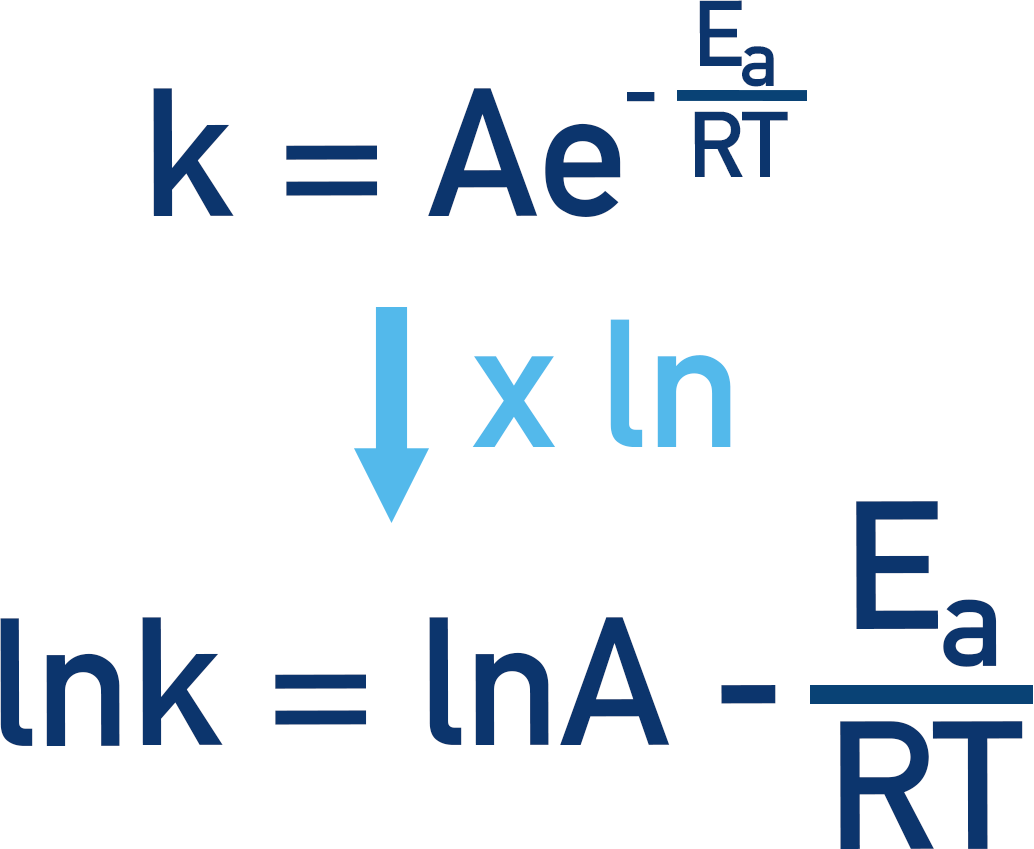
Unlike in the original form of the expression (with e), plots of these values would give a straight-line graph (see Arrhenius Equation).
For straight-line graphs, the line always follows a general equation y = mx + c. Where m is the gradient of the line (change in y / change in x) and c is a constant value that never changes.
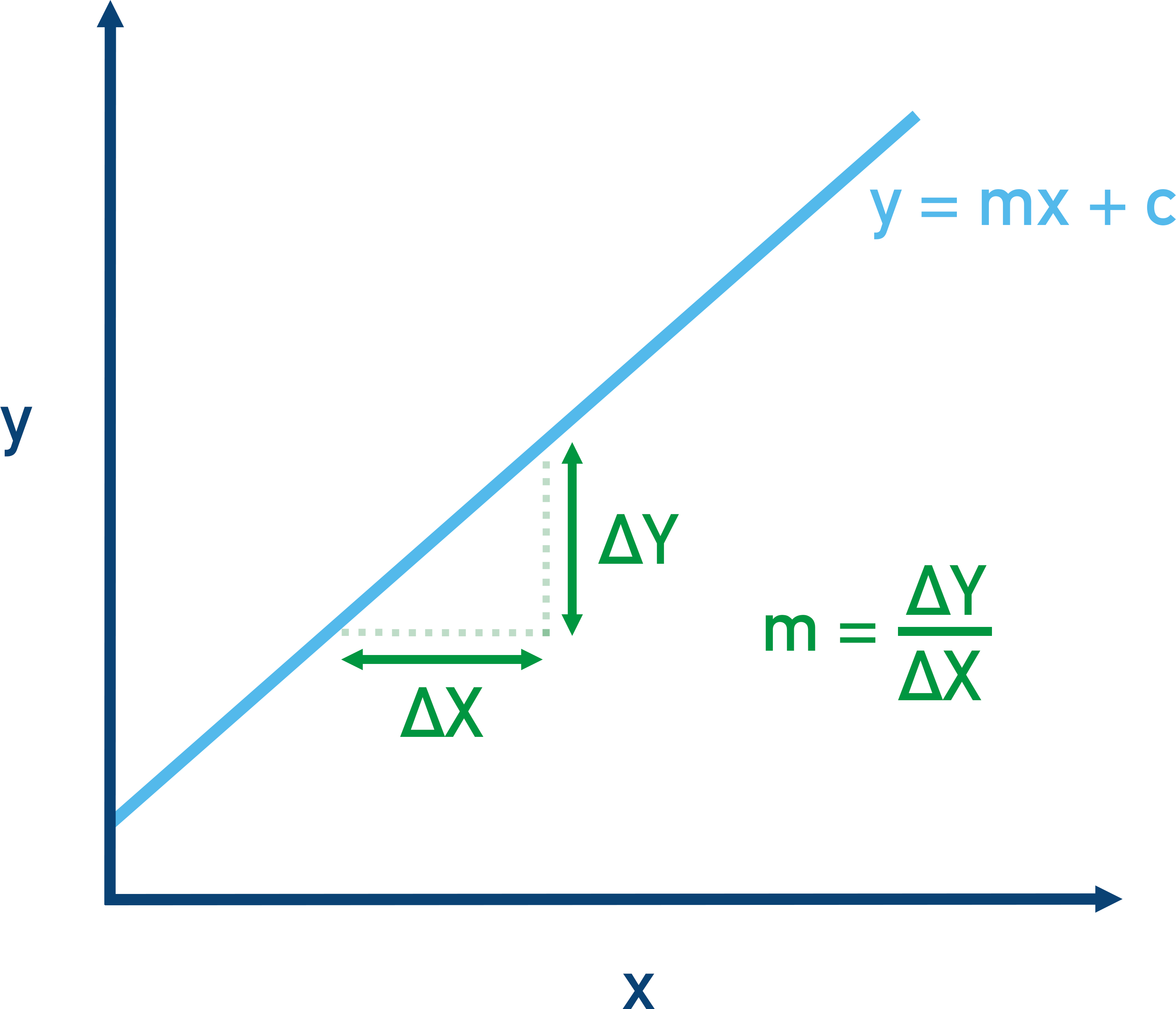
It can be difficult for students to see sometimes, but the ln form of the Arrhenius equation actually is a form of y = mx + c
For y = mx + c, the c is a constant – this means the value never changes. In the Arrhenius equation, A is also a constant that never changes (meaning lnA will also be a constant value).
We can therefore rearrange the equation to be:

This now follows the y = mx + c pattern. Where y = lnk and c = lnA
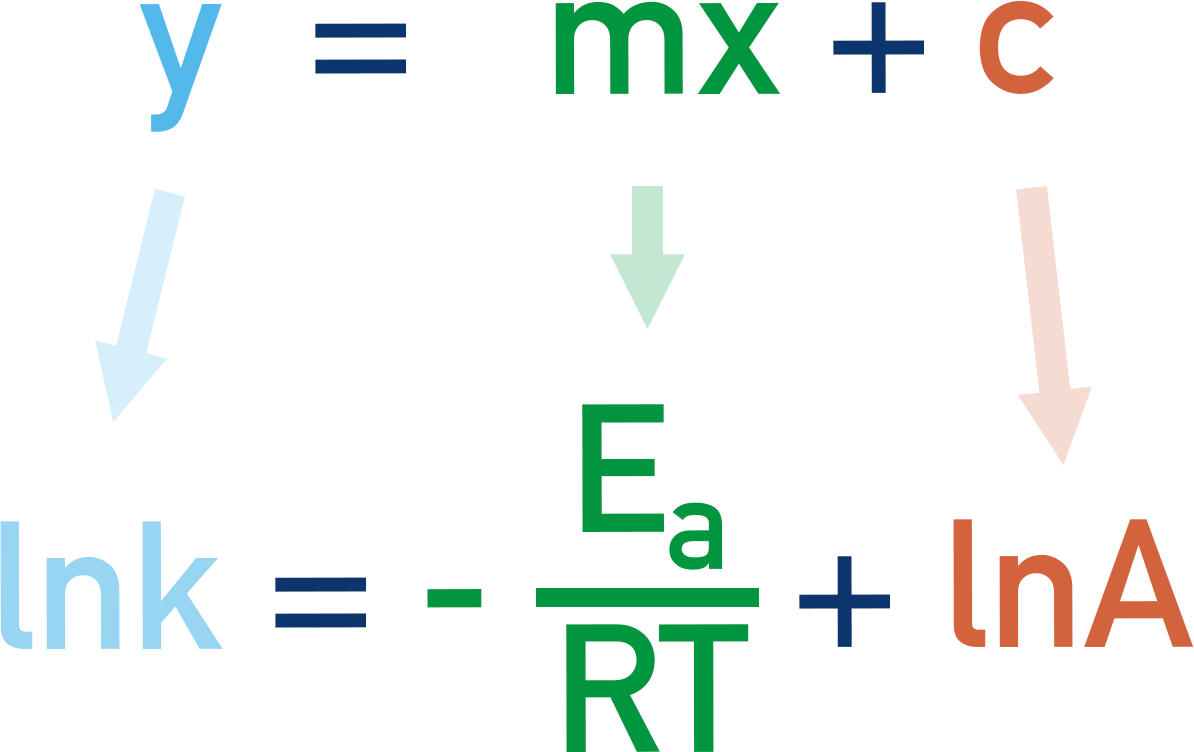
This means that –Ea/RT is ‘mx’
The problem is –Ea/RT doesn’t look like it has an x or an m component! To show them, we have to write it in a slightly different form.
-Ea/RT is the same as –Ea/R x 1/T
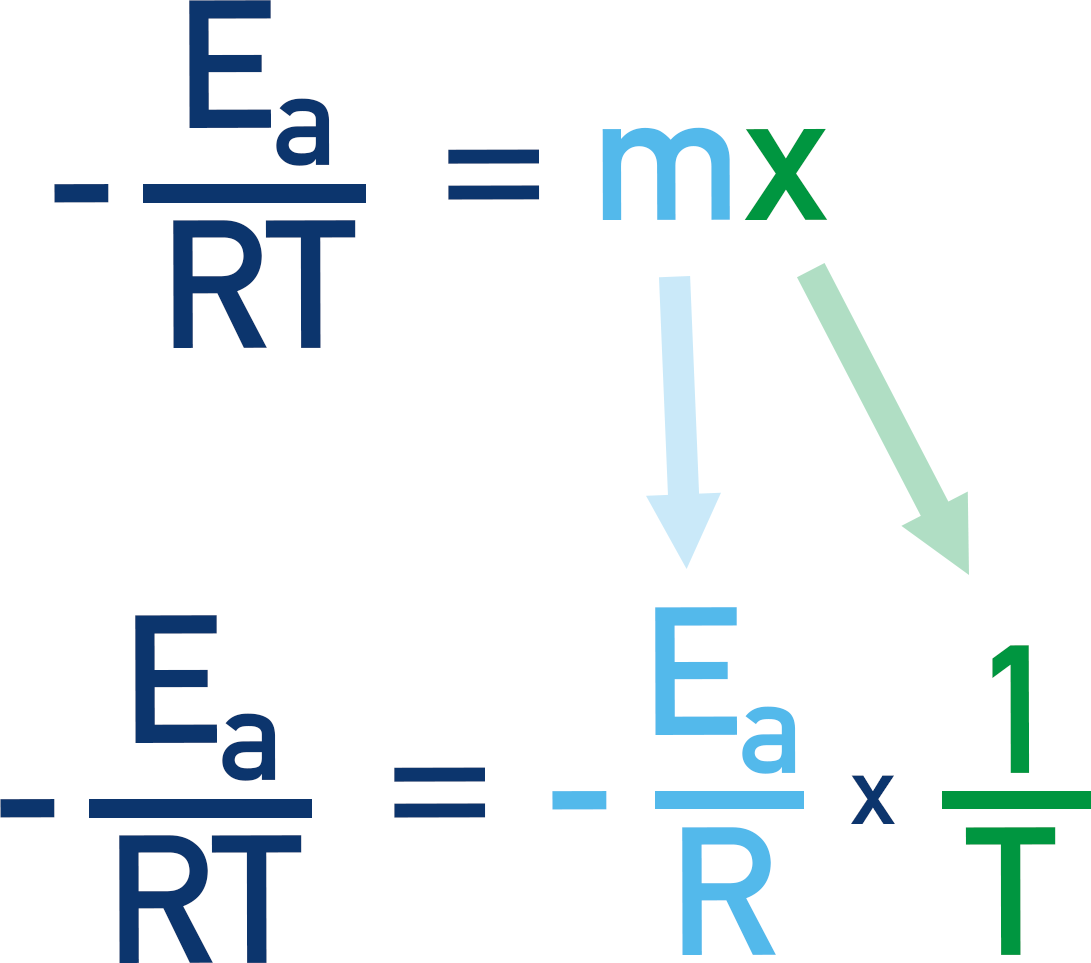
Now, we have the form of the Arrhenius equation as:
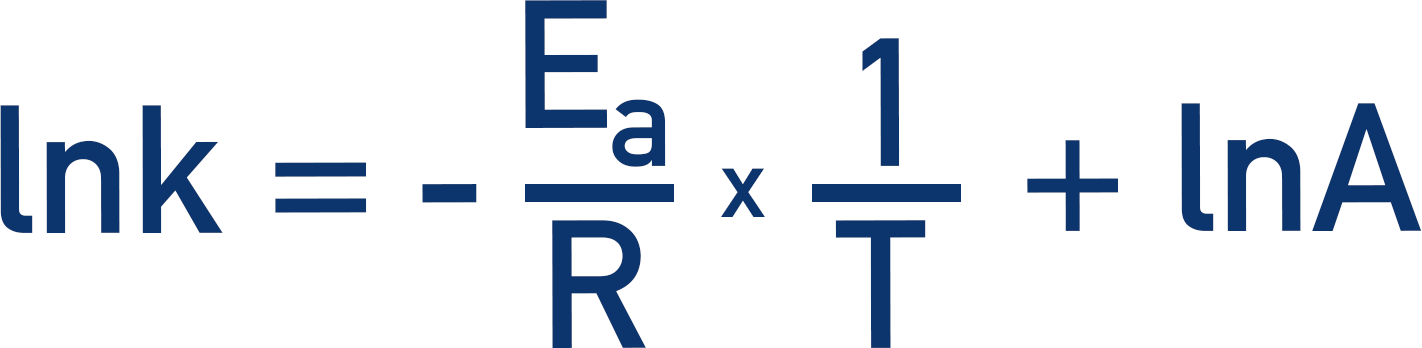
This looks like y = mx + c
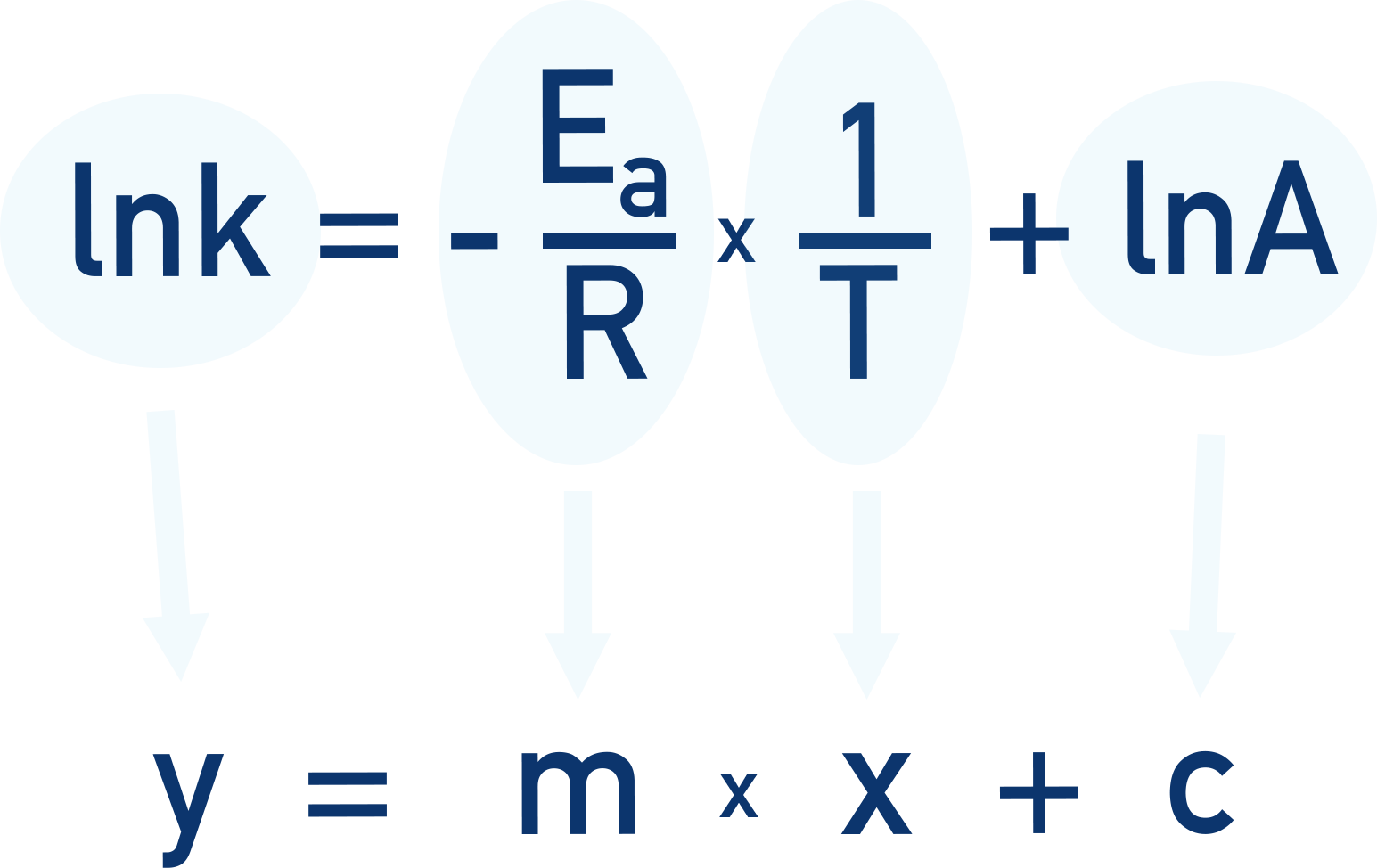
Where y = lnk, x = 1/T, c = lnA and m (the gradient) = -Ea/R
Just like m = (y/x) – c, the Arrhenius equation can be rearranged to find activation energy:
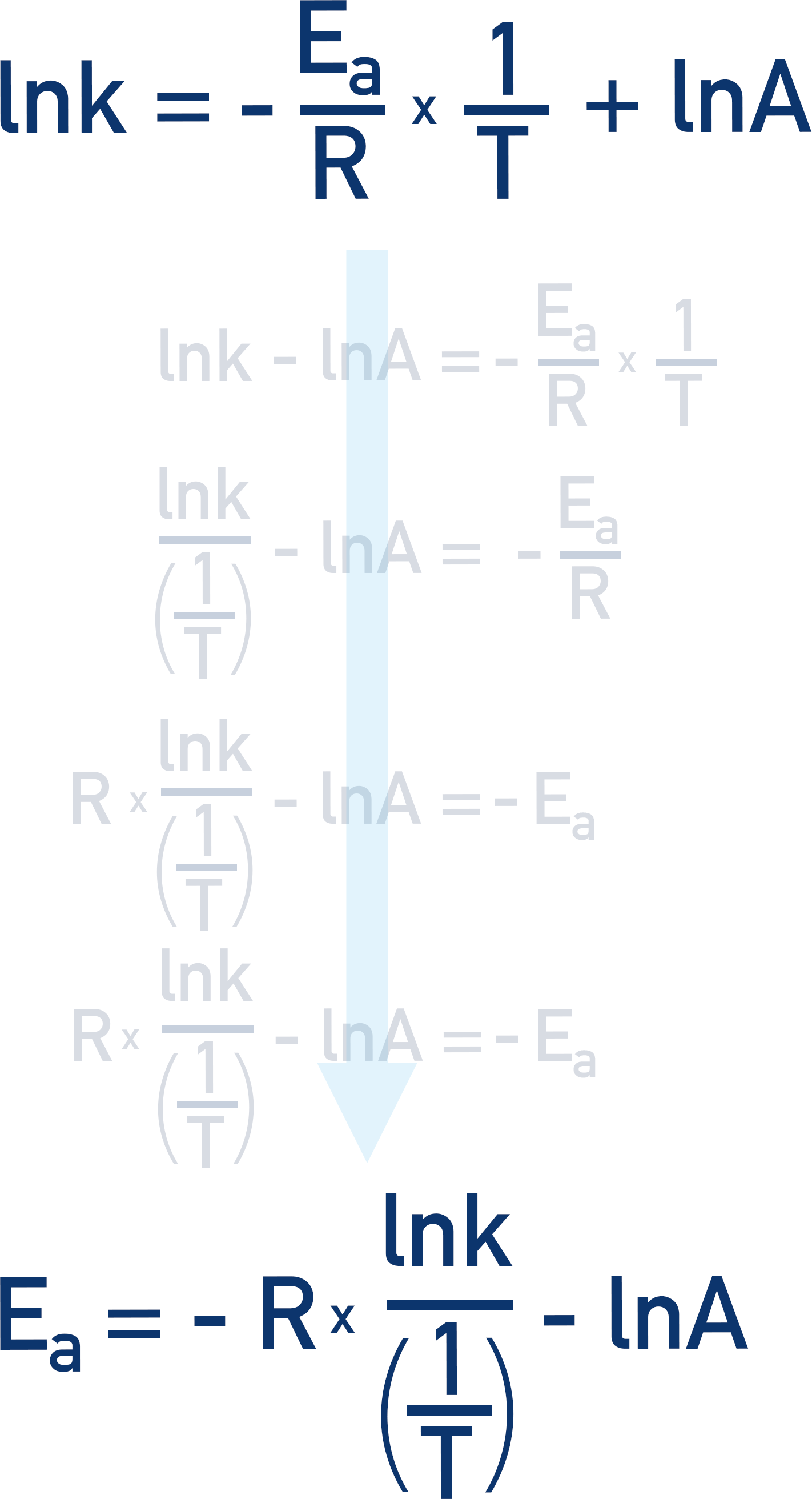
How to use a Graph to Find Activation Energy, Ea
A common use of the Arrhenius equation is to find the activation energy of a reaction using values for the rate constant (k) at different temperatures.
If we know that lnk = -Ea/R x (1/T) + lnA, we can treat it in the same way as y = mx + c (see above). And m, the gradient, will be the same as –Ea/R.
Now, all we have to do is plot a graph using y and x values. y = lnk and x = 1/T
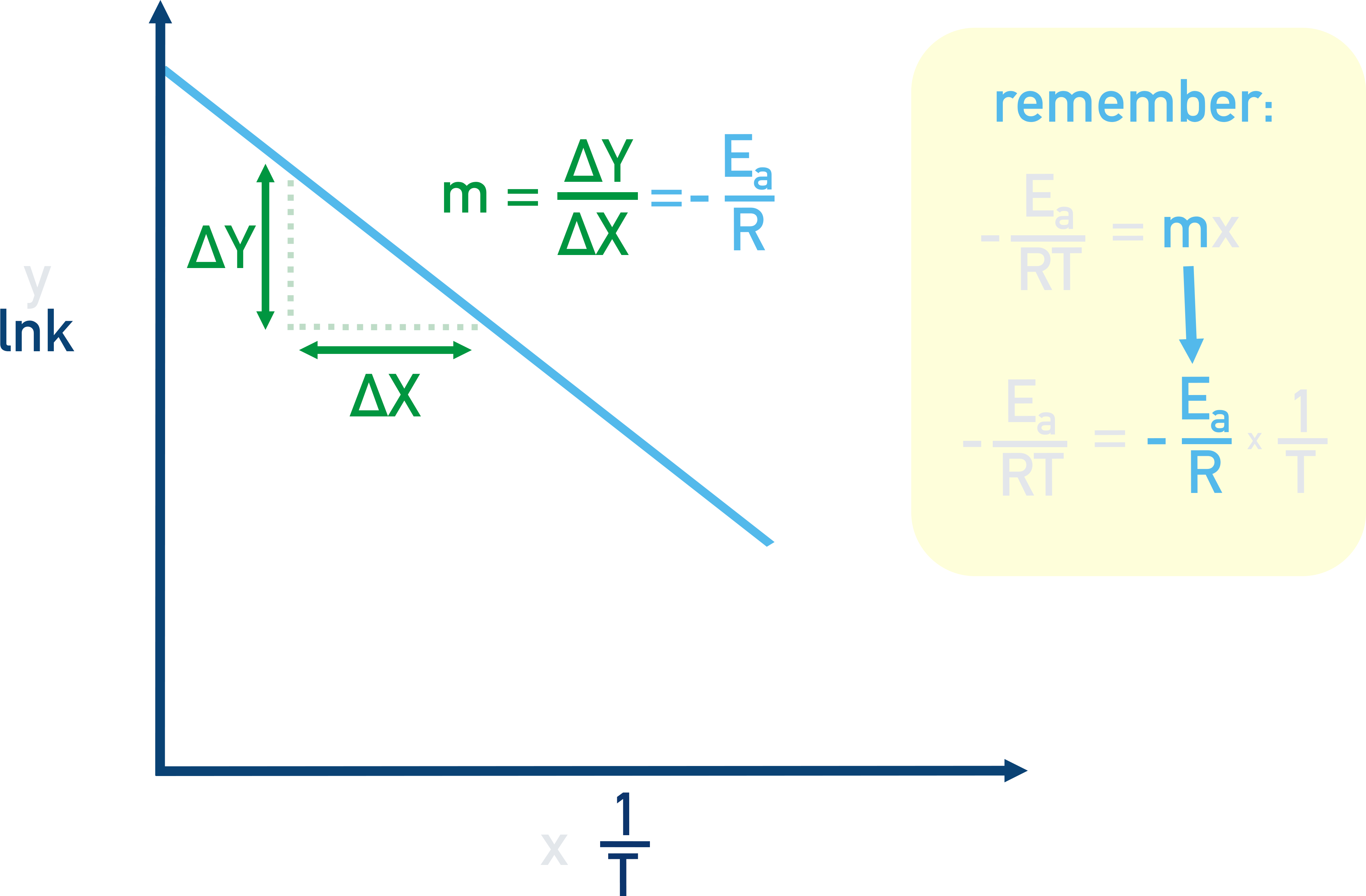
When these have been plotted, the graph should be a straight line and the gradient = -Ea/RT.
The gradient of a straight line can be calculated by the change in y / change in x.
Meaning the change in y / change in x = -Ea/R
R is a constant (8.31 J K-1mol-1)
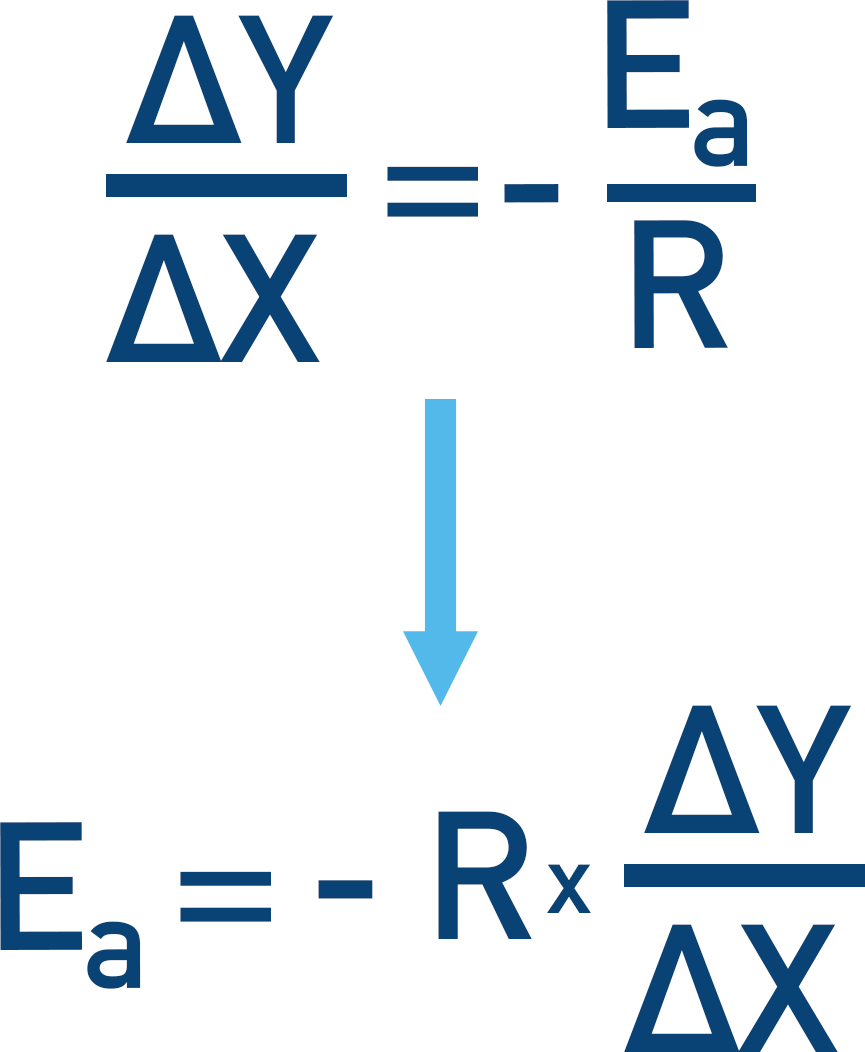
Note, the line for an Arrhenius plot will have a negative gradient (downwards slope), this is correct as the gradient = -Ea/RT.
Example Question
Using the following data, find the activation energy and calculate the value of A.
| Temperature, T (in Kelvin, K) |
Rate Constant, k |
|---|---|
| 450 | 2.50 x 10-5 |
| 475 | 5.23 x 10-5 |
| 500 | 6.37 x 10-4 |
| 525 | 3.01 x 10-3 |
| 550 | 1.47 x 10-2 |
To answer this, we need to plot an Arrhenius plot (see above). Using the Arrhenius equation in the form:
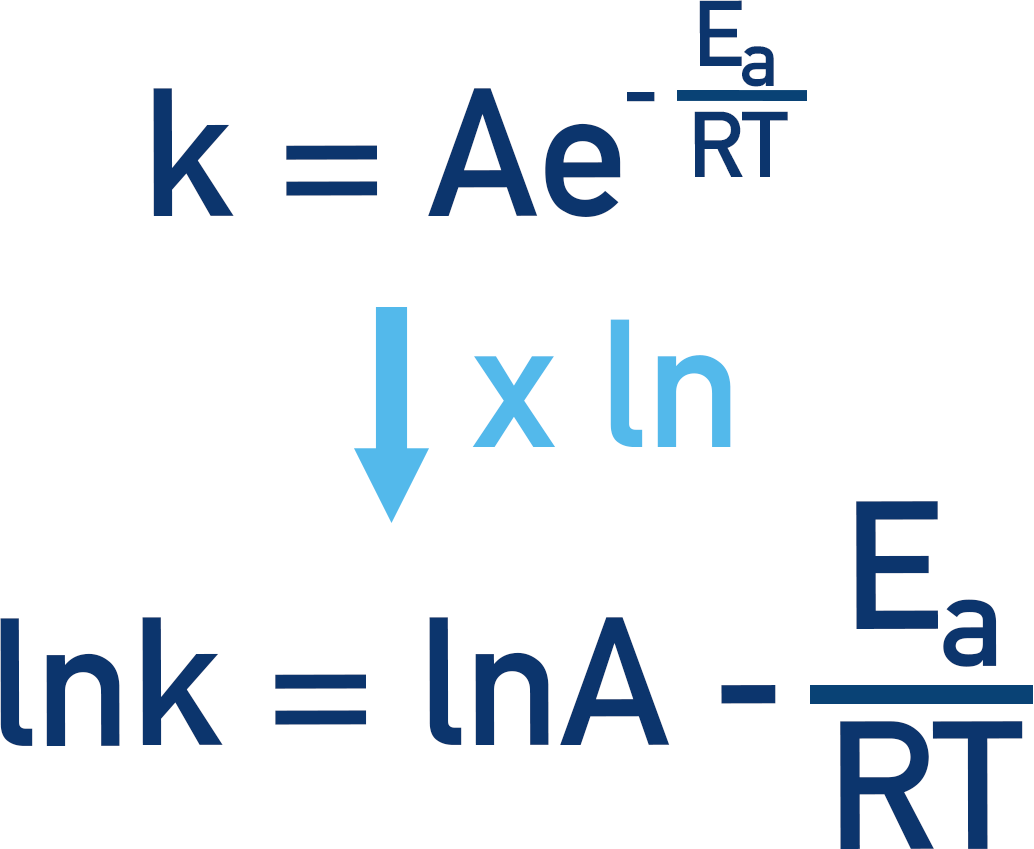
Remember this is the same as:
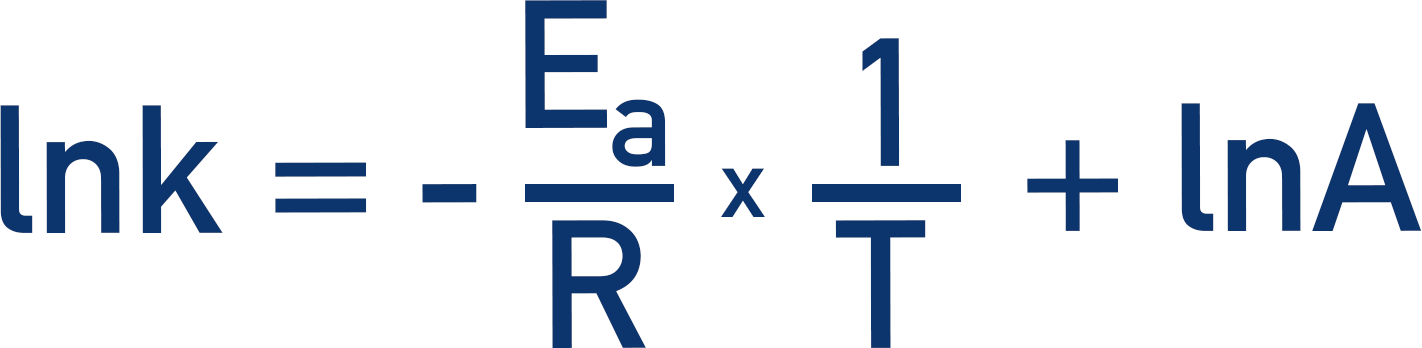
This is to enable us to treat the expression as y = mx + c:
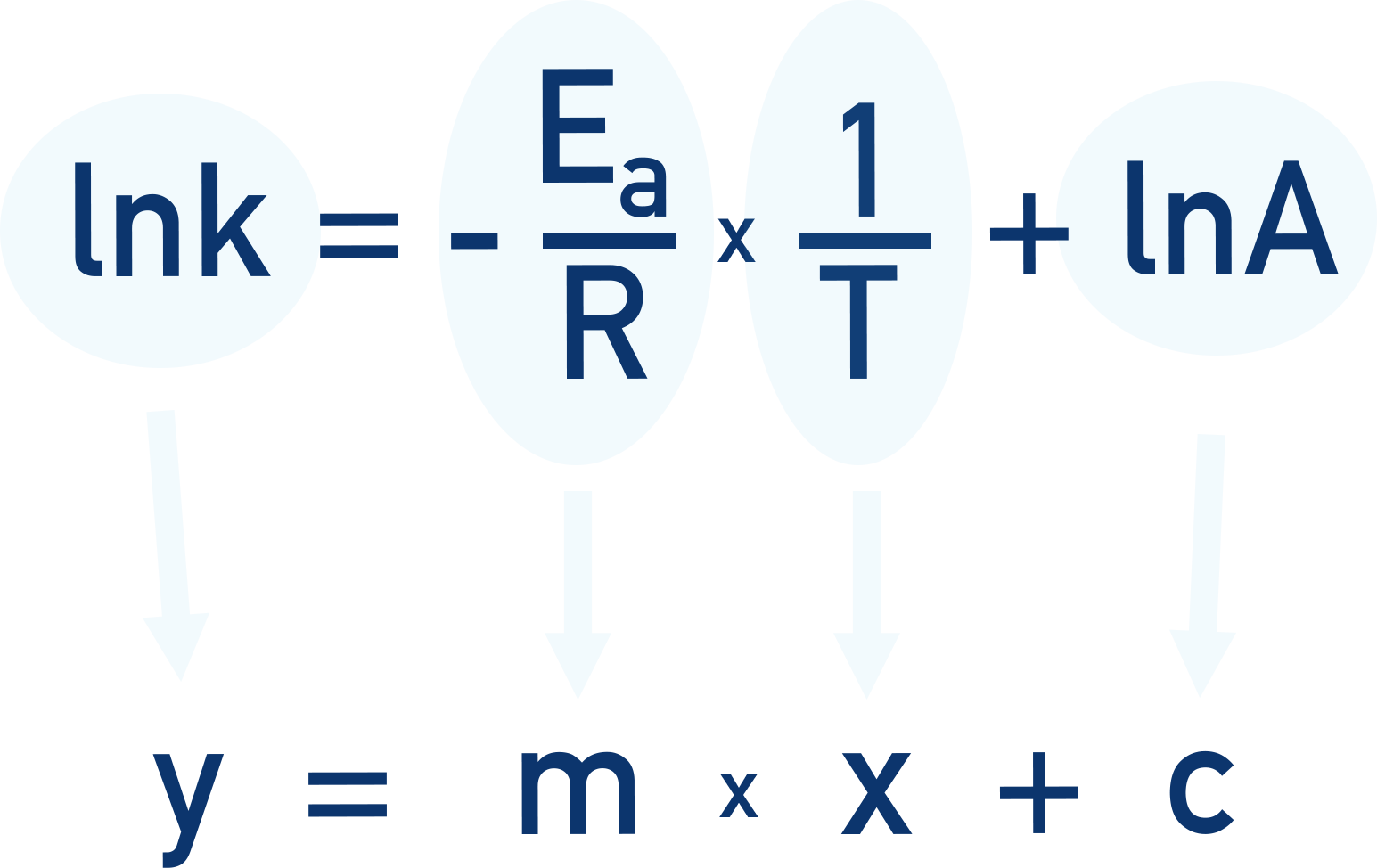
The first thing we need to do is find lnk and 1/T as then we can plot a graph with lnk as the y axis, 1/T as the x axis.
| Temperature, T (in Kelvin, K) |
1/T | Rate Constant, k | lnk |
|---|---|---|---|
| 450 | 2.22 x 10-3 | 2.50 x 10-5 | -10.6 |
| 475 | 2.11 x 10-3 | 5.23 x 10-5 | -9.86 |
| 500 | 2.00 x 10-3 | 6.37 x 10-4 | -7.36 |
| 525 | 1.90 x 10-3 | 3.01 x 10-3 | -5.81 |
| 550 | 1.82 x 10-3 | 1.47 x 10-2 | -4.22 |
Plot a graph lnk as y and 1/T as x:
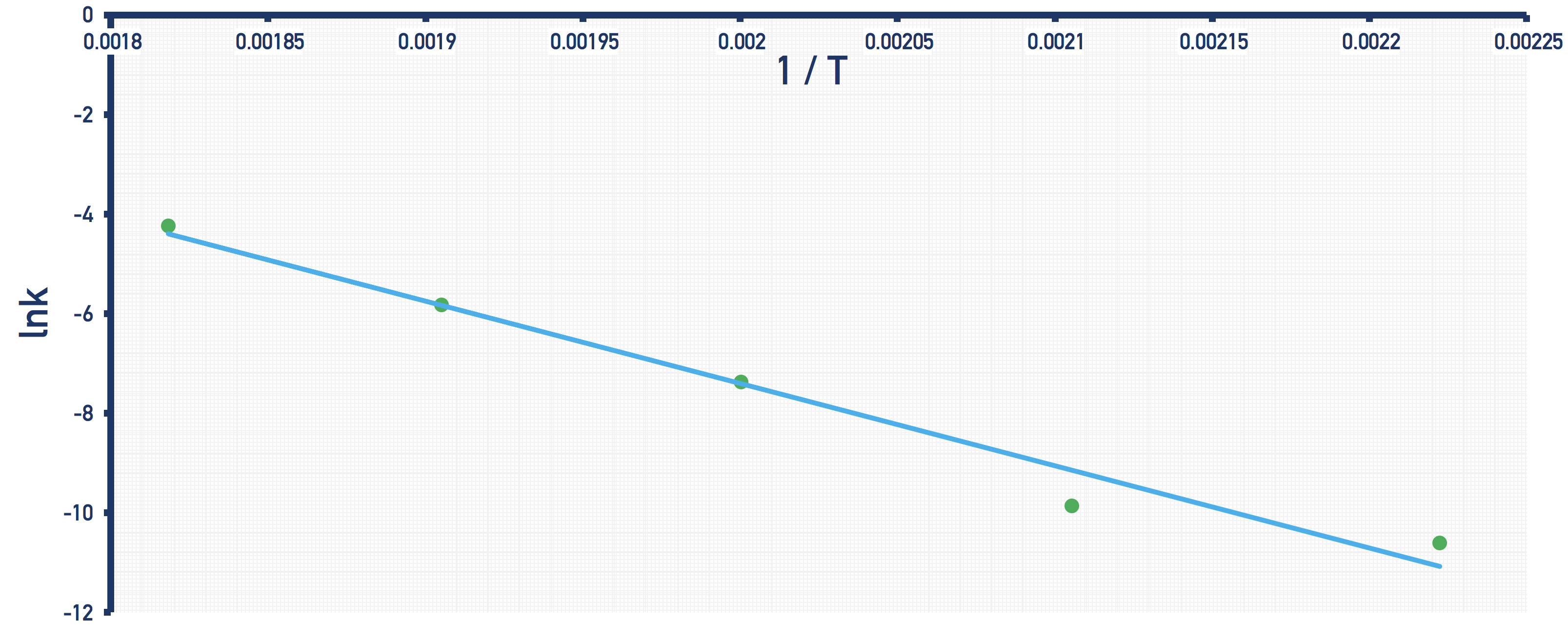
We now need to find the gradient of the line ‘m’:
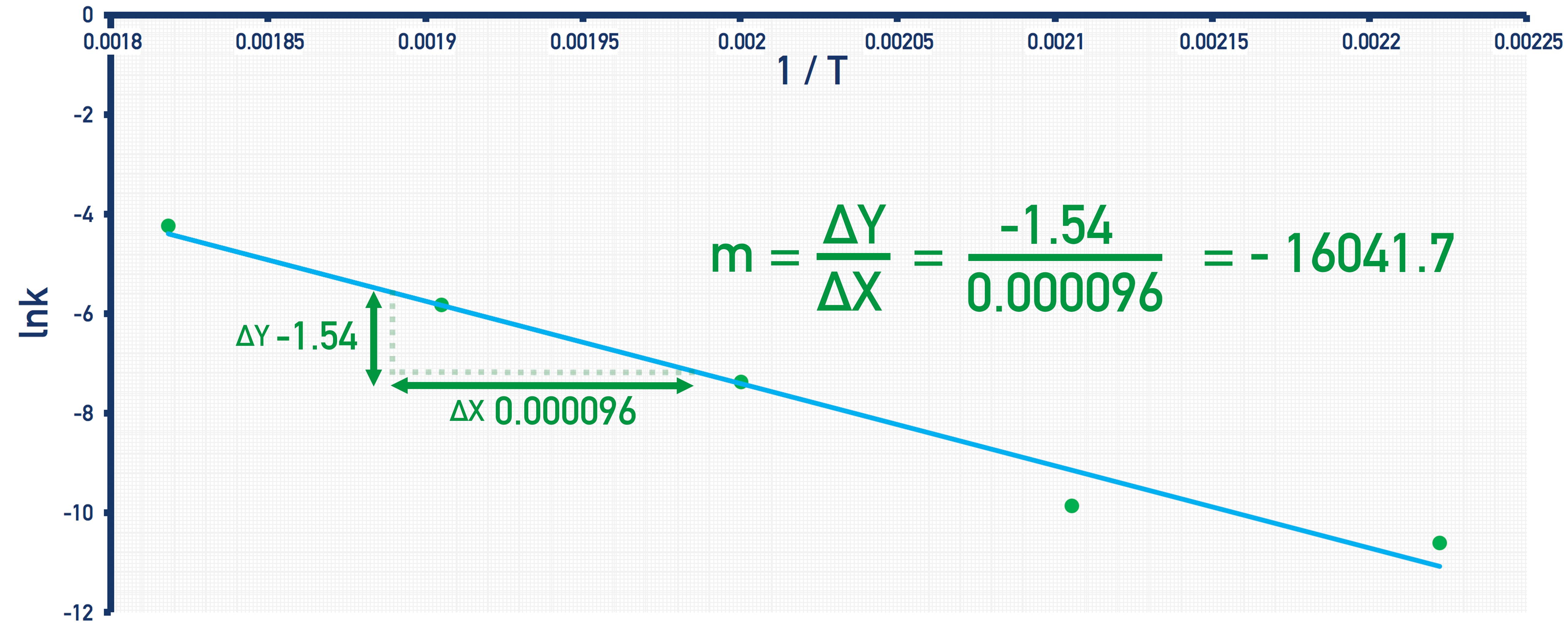
Now we have the gradient of the line, we can calculate Ea.
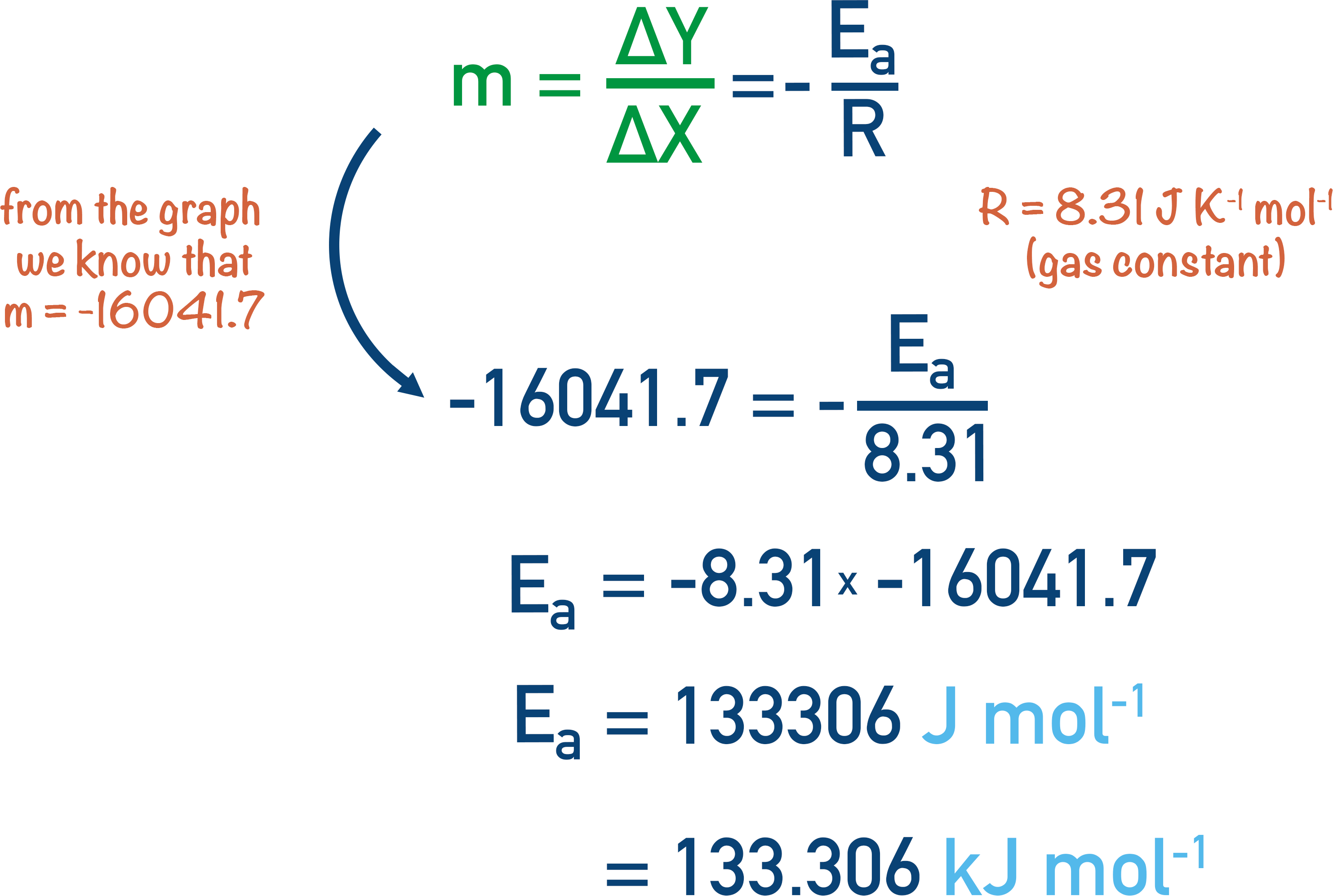
Note, the units for Ea are J mol-1 due to the units of the gas constant being in J. To get activation energy into kJ, divide by 1000.
The second part of the question is to find the Arrhenius constant (A):
This is now just a question of substituting in the values we know for all the values into the Arrhenius expression. Remember lnA is the same as c (see above).
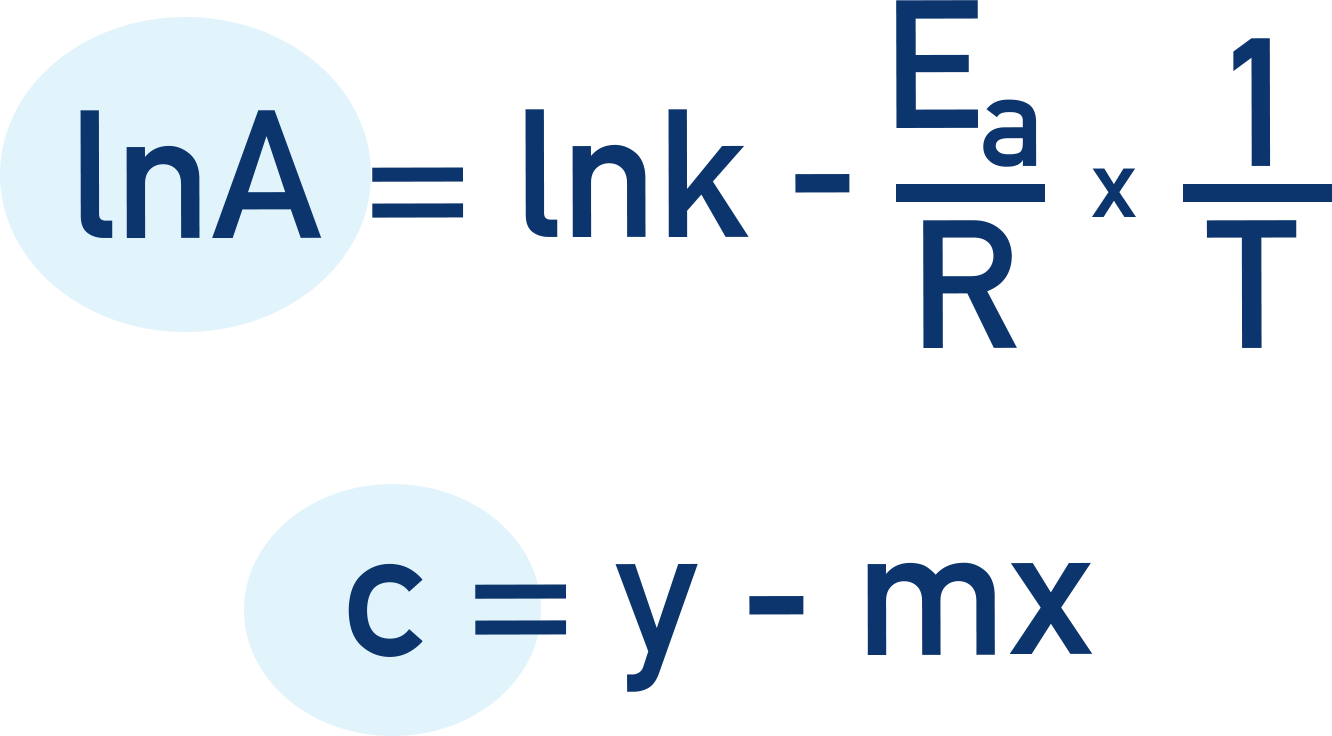
By taking any values for lnk and 1/T, we can substitute the values into the expression and find lnA.
Using 1/T as 2.22 x 10-3 and lnk = -10.6
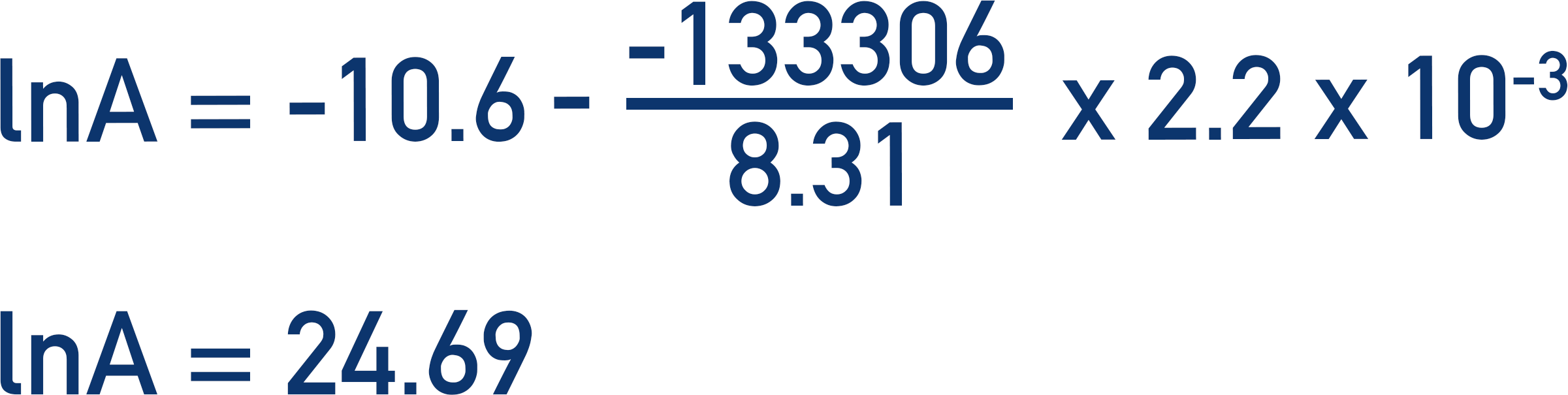
The final thing left to do is convert lnA to A. To do this, we use ‘e’.
For details on natural logarithms see Arrhenius Equation.
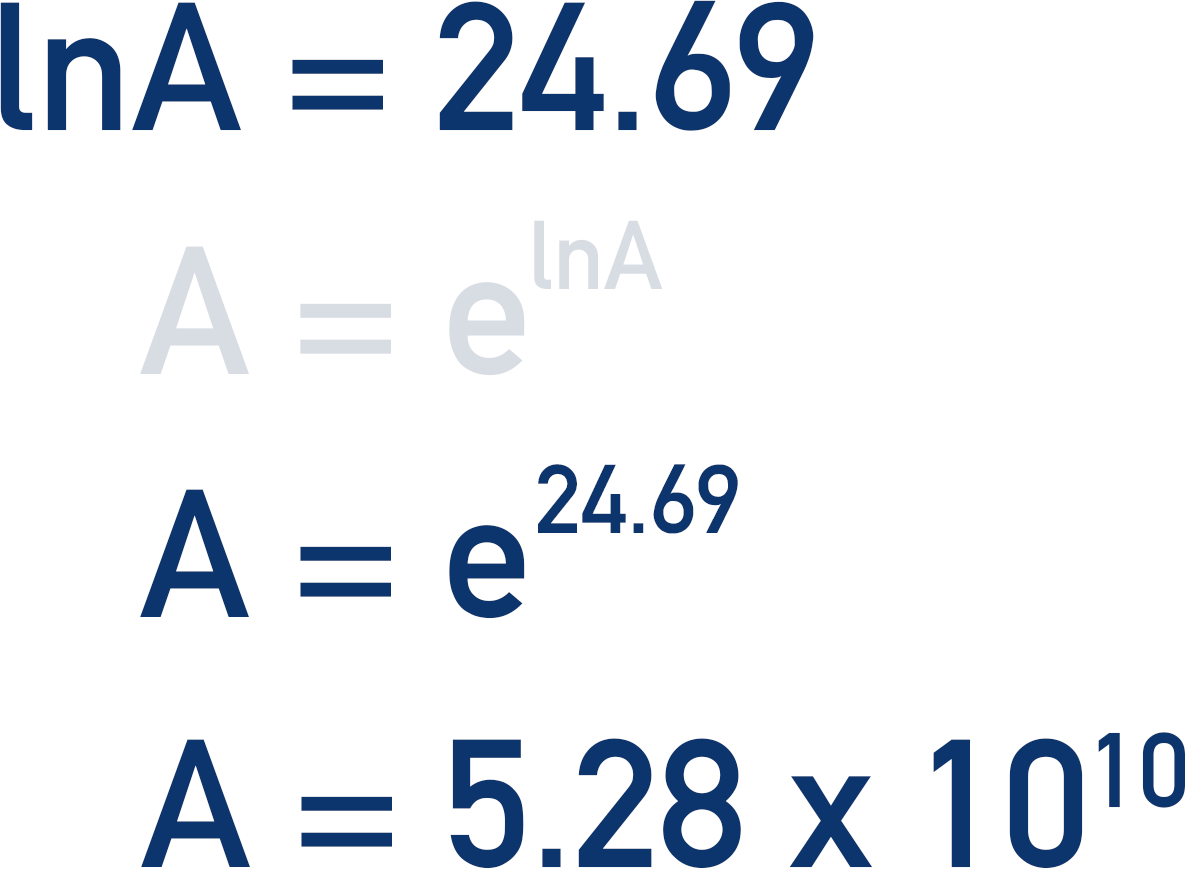
Note, this is only the value for A. The units for A are entirely based on the units for the rate constant k. The units for k are the same for A.
