Born–Haber Cycles HL Only
Quick Notes
- A Born–Haber cycle is a Hess’s Law diagram showing energy changes in forming an ionic compound from its elements.
- They can be used to calculate or determine:
- Enthalpy of formation (ΔHf⦵)
- Lattice enthalpy (ΔHlatt⦵)
- Ionisation energy (IE)
- Electron affinity (EA)
- Enthalpy of atomisation (ΔHat⦵)
Full Notes
What Is a Born–Haber Cycle?
A Born–Haber cycle breaks down the formation of an ionic compound into a series of theoretical steps. It applies Hess’s Law to calculate one unknown energy change (often lattice enthalpy or enthalpy of formation).
Each step corresponds to a real or theoretical process in forming the ionic solid from its elements in standard states.
Standard Born–Haber Cycles Often Include
- Enthalpy of Formation (ΔHf⦵):
Energy change when 1 mole of an ionic compound forms from its elements in standard states.
Example: Na (s) + ½Cl₂ (g) → NaCl (s) - Enthalpy of Atomisation (ΔHat⦵):
Energy change when 1 mole of gaseous atoms forms from an element.
Example:Na (s) → Na (g)
½Cl₂ (g) → Cl (g) - 1st Ionisation Energy (IE):
Energy required to remove 1 mole of electrons from 1 mole of gaseous atoms of an element (to form 1 moles worth of ions with a 1+ charge).
Example: Na (g) → Na⁺ (g) + e⁻ - Bond Enthalpy:
Energy required to break one mole of a covalent bond in gaseous molecules.
Example: Cl₂ (g) → 2Cl (g) - 1st Electron Affinity (EA):
Energy change when 1 mole of gaseous atoms gains electrons to form 1 moles worth of ions with a 1− charge.
Example: Cl (g) + e⁻ → Cl⁻ (g) - Lattice Enthalpy (ΔHlatt⦵):
Energy change when 1 mole of an ionic lattice forms or dissociates from gaseous ions. This is often the unknown value we solve for.

You won’t be asked to construct a complete Born–Haber cycle in an exam, however you do need to be aware of how to construct them in order to understand how they work!
Example: Born–Haber Cycle for NaCl
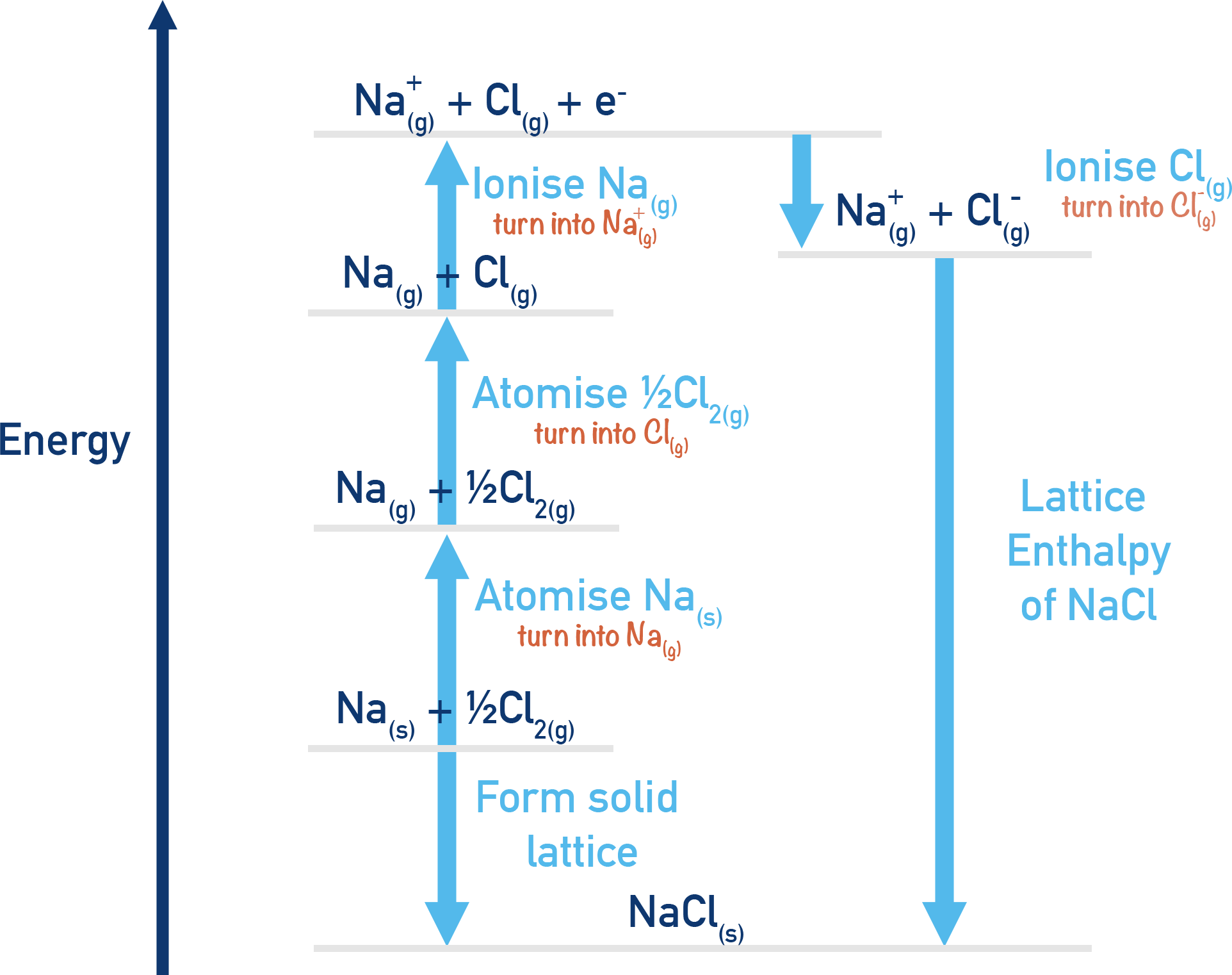
- Step 1: Formation of NaCl (ΔHf⦵):Na (s) + ½Cl₂ (g) → NaCl (s)
- Step 2: Atomisation of Na (ΔHat⦵): Na (s) → Na (g)
- Step 3: Atomisation of Cl₂ (ΔHat⦵):½Cl₂ (g) → Cl (g)
- Step 4: Ionisation Energy of Na (IE₁):Na (g) → Na⁺ (g) + e⁻
- Step 5: Electron Affinity of Cl (EA₁): Cl (g) + e⁻ → Cl⁻ (g)
- Step 6: Lattice Enthalpy (ΔHlatt⦵):Na⁺ (g) + Cl⁻ (g) → NaCl (s)
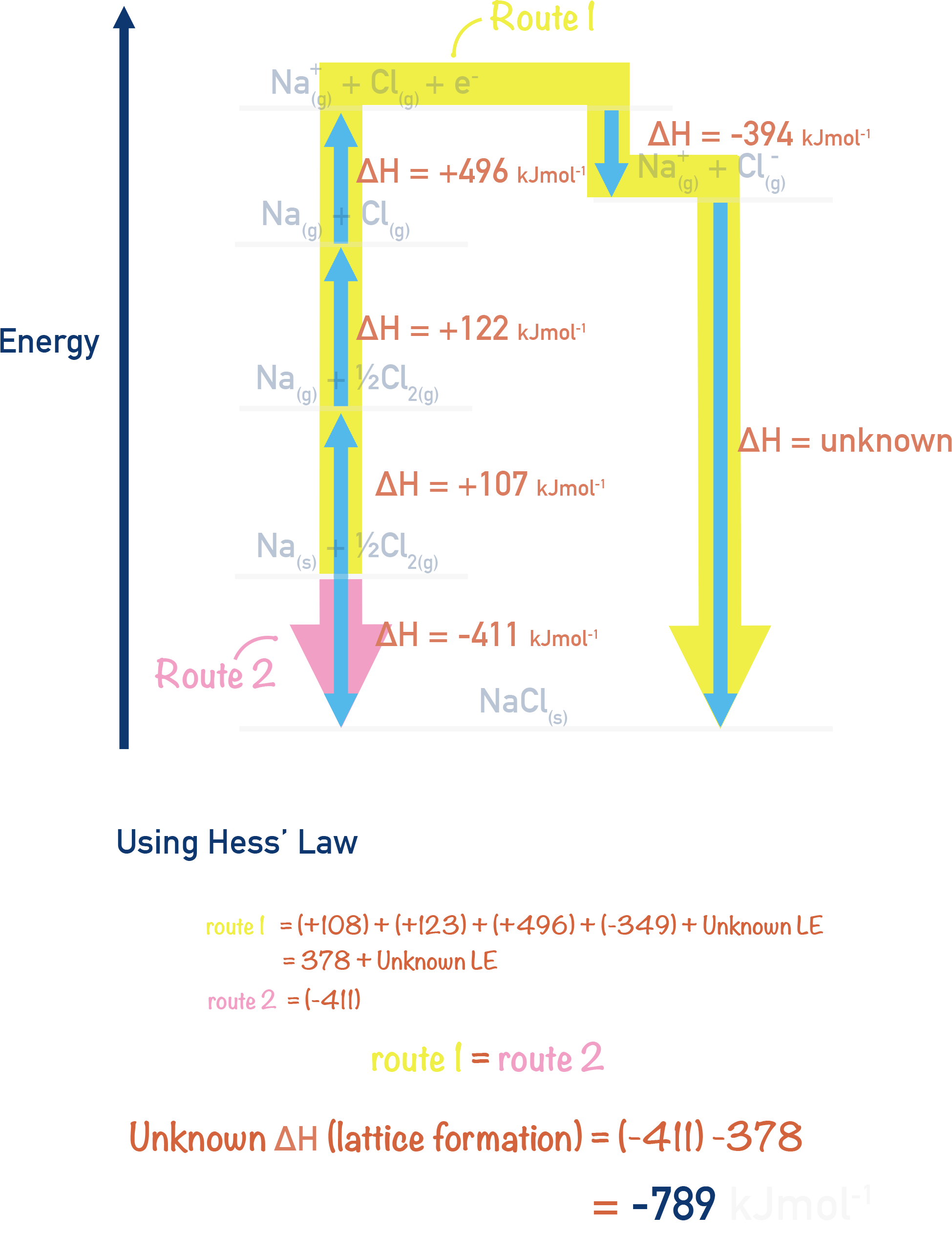
By rearranging these enthalpy changes and substituting experimental values into the cycle we can use Hess’s Law to calculate ΔHlatt⦵.
Summary Table
| Energy Change | Process | Equation |
|---|---|---|
| ΔHf⦵ | Formation | Na (s) + ½Cl₂ (g) → NaCl (s) |
| ΔHat⦵ | Atomisation of Na | Na (s) → Na (g) |
| ΔHat⦵ | Atomisation of Cl₂ | ½Cl₂ (g) → Cl (g) |
| IE₁ | Ionisation Energy | Na (g) → Na⁺ (g) + e⁻ |
| EA₁ | (1st) Electron Affinity | Cl (g) + e⁻ → Cl⁻ (g) |
| ΔHlatt⦵ | Lattice Enthalpy | Na⁺ (g) + Cl⁻ (g) → NaCl (s) |
Summary
- A Born–Haber cycle applies Hess’s Law to ionic compound formation.
- It includes enthalpy of formation, atomisation, ionisation, electron affinity, and lattice enthalpy.
- Lattice enthalpy is often the unknown calculated value.
What are the factors that influence the strength of lattice enthalpy in an ionic compound?
Lattice enthalpy is affected by:
- Ion charge: Higher charges result in stronger electrostatic attraction, increasing lattice enthalpy.
- Ion size (radius): Smaller ions pack more closely, strengthening attractions and increasing lattice enthalpy.
Therefore, compounds with small, highly charged ions (e.g. MgO) have much higher lattice enthalpies than those with larger or singly charged ions (e.g. NaCl).
