Using Mole Ratios to Calculate Masses, Volumes and Concentrations

Specification Reference R2.1.2

Quick Notes

Mole ratios come from balanced chemical equations.
Used to calculate:
- Masses of reactants/products
- Volumes of gases (using molar volume)
- Concentrations in solution
Key equations:
- n = m / M (mass to moles)
- n = C × V (concentration × volume)
Molar volume of gas at STP = 22.7 dm³ mol⁻¹.
Use A_r values from the IB data booklet to two decimal places.

Full Notes

Mole Ratios from Chemical Equations

The balanced equation gives the stoichiometric ratio of moles of each substance involved.

For Example:

2H₂(g) + O₂(g) → 2H₂O(l)

Mole ratio: 2 : 1 : 2 (H₂ : O₂ : H₂O)

Converting Between Mass and Moles

To calculate reacting masses or product yield:

Step 1: Use the molar mass (M) from the periodic table (A_r or M_r).
Step 2: Use n = m / M to find moles.
Step 3: Use mole ratio from the equation.
Step 4: Use m = n × M to get the mass required or produced.

Worked Example

How many grams of water are formed when 4 g of hydrogen reacts completely with oxygen?

Balanced equation: 2H₂ + O₂ → 2H₂O
M(H₂) = 2.02 g mol⁻¹ → n(H₂) = 4 / 2.02 ≈ 1.98 mol
From the equation, 2 mol H₂ → 2 mol H₂O → so n(H₂O) = 1.98 mol
M(H₂O) = 18.02 g mol⁻¹ → m(H₂O) = 1.98 × 18.02 ≈ 35.7 g

Using Volume for Gases (at STP)

At standard temperature and pressure (STP):

1 mole of any gas occupies 22.7 dm³
This means we can use: n = volume / 22.7
to convert volume of a gas to moles

Worked Example

What volume of O₂ is needed to combust 5.0 g of CH₄?

Equation: CH₄ + 2O₂ → CO₂ + 2H₂O
M(CH₄) = 16.04 g mol⁻¹ → n = 5.0 / 16.04 ≈ 0.312 mol
Mole ratio CH₄ : O₂ = 1 : 2 → O₂ needed = 0.624 mol
Volume = 0.624 × 22.7 ≈ 14.2 dm³

Concentration Calculations (Solutions)

When dealing with solutions, concentration is the amount of a substance (in moles) per 1 dm³ of solution. Common units: mol dm⁻³.

Moles from Concentration and Volume

Worked Example

What is the concentration of a solution made by dissolving 0.1 mol of NaOH in 250 cm³ of solution?

Volume = 250 ÷ 1000 = 0.250 dm³
Concentration = 0.1 ÷ 0.250 = 0.4 mol dm⁻³

Matt’s Exam Tip

Make sure volume is always in dm³ when using these formulas (divide cm³ by 1000 to do this).

Summary

Mole ratios from equations allow calculation of masses, volumes and concentrations.
Use n = m / M for masses, n = C × V for solutions, and 22.7 dm³ mol⁻¹ for gases at STP.
Always balance equations and check unit conversions.

Linked Course Questions

Structure 1.5 — Linked Course Question

How does the molar volume of a gas vary with changes in temperature and pressure?

The molar volume of a gas increases with temperature and decreases with pressure, following the ideal gas law (PV = nRT).

If temperature increases, particles move faster and occupy more space meaning volume increases.

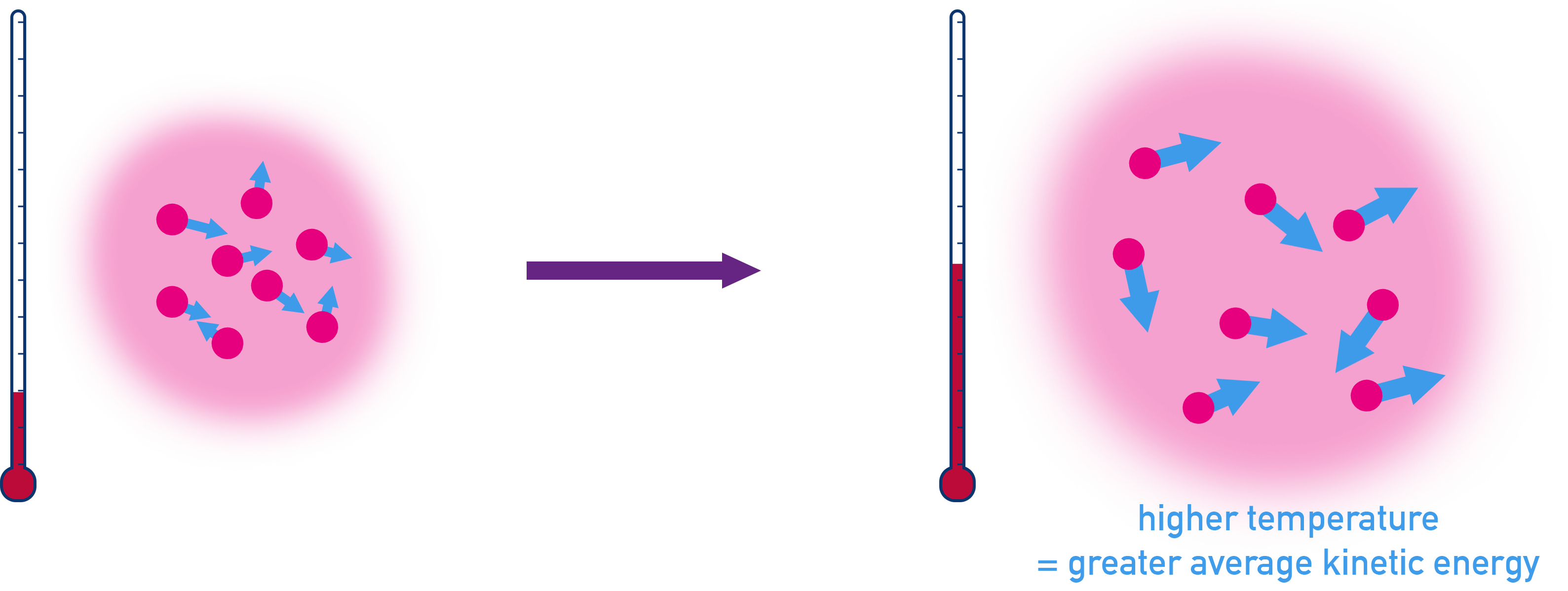
IB Chemistry diagram showing how higher temperature increases kinetic energy and molar volume of gas particles.

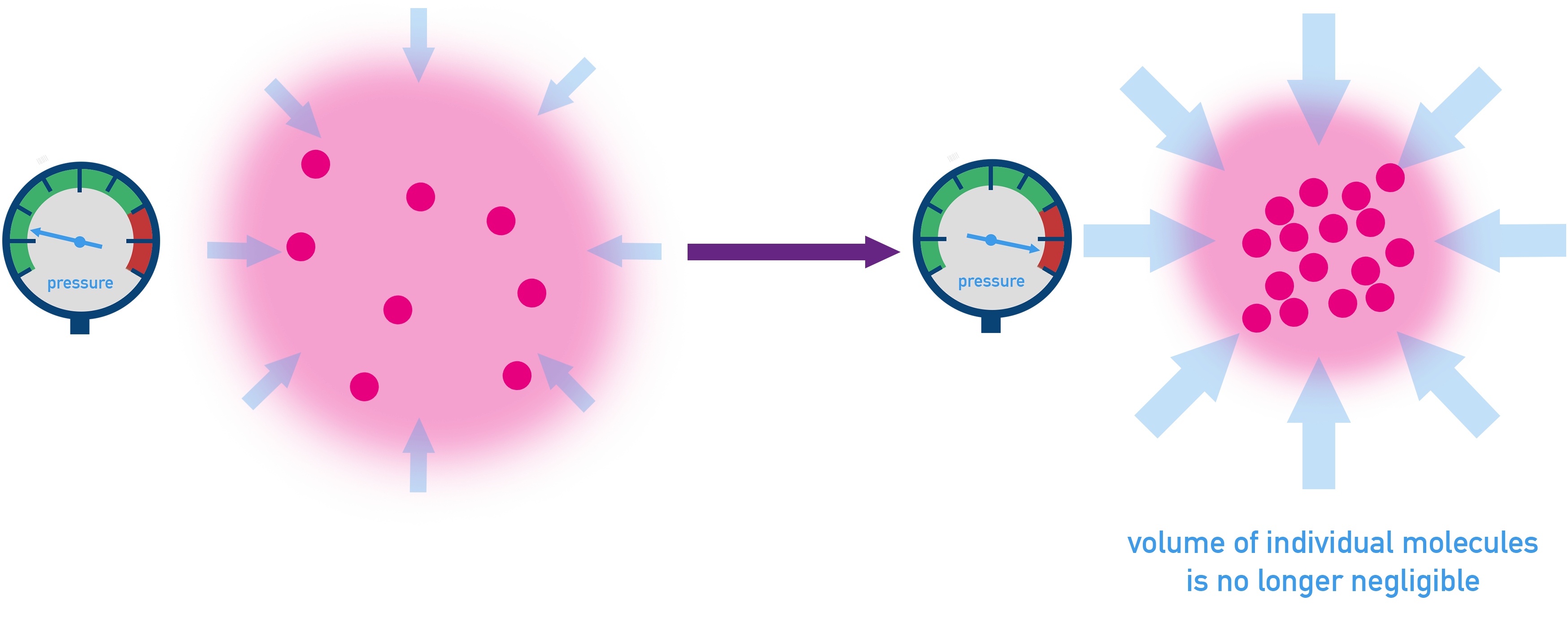
If pressure increases, gas particles are compressed into a smaller space meaning volume decreases.

IB Chemistry diagram showing how increasing pressure reduces gas volume by compression of particles.

Nature of Science, Structure 1.4 — Linked Course Question

In what ways does Avogadro’s law help us to describe, but not explain, the behaviour of gases?

Avogadro’s law describes how gases behave under many conditions, stating that equal volumes of gases at the same temperature and pressure contain equal numbers of particles. However, it does not explain why gases behave this way, nor account for differences in particle size, mass, or intermolecular forces.

In reality, gases often show non-ideal behaviour at high pressures or low temperatures where intermolecular forces and particle volume matter. Avogadro’s law is therefore a simplified model, useful for descriptions but not a full explanation.