Entropy (S) and Entropy Changes (ΔS⦵) HL Only
Quick Notes
- Entropy (S) measures the dispersal of energy and matter in a system.
- The more disorder or randomness, the higher the entropy.
- Entropy order (same conditions): Gases > Liquids > Solids
- Entropy increases when:
- A solid melts or evaporates.
- A gas is produced in a reaction.
- A substance dissolves.
- Entropy decreases when:
- Gases condense or liquids freeze.
- Fewer particles are formed from more.
- Standard entropy change: ΔS⦵ = ΣS⦵(products) – ΣS⦵(reactants)
- Entropy values (S⦵) are given in J mol⁻¹ K⁻¹.
- S = 0 for a perfect crystal at 0 K (Third Law of Thermodynamics).
Full Notes
What Is Entropy (S)?
Entropy is a thermodynamic quantity that describes the dispersal or distribution of matter and energy within a system.
In simpler terms – the more ways the particles or energy can be arranged, the greater the entropy.
Entropy is a state function, measured in J mol⁻¹ K⁻¹.
Change in Entropy (ΔS) measures how the disorder of a system changes for a reaction or process.
Trends in Entropy by Physical State
Under the same temperature and pressure:
- Solids have the lowest entropy (particles vibrate in fixed positions).
- Liquids have higher entropy (particles can move more freely).
- Gases have the highest entropy (particles are far apart and move independently).
Therefore: S (gas) > S (liquid) > S (solid)
Predicting Entropy Changes
We can often predict whether entropy increases or decreases in a physical or chemical process:
Changes of state

Going from a solid to a liquid or a gas increases entropy because particles move more freely and can be arranged in more possible ways.
Dissolving ionic solids
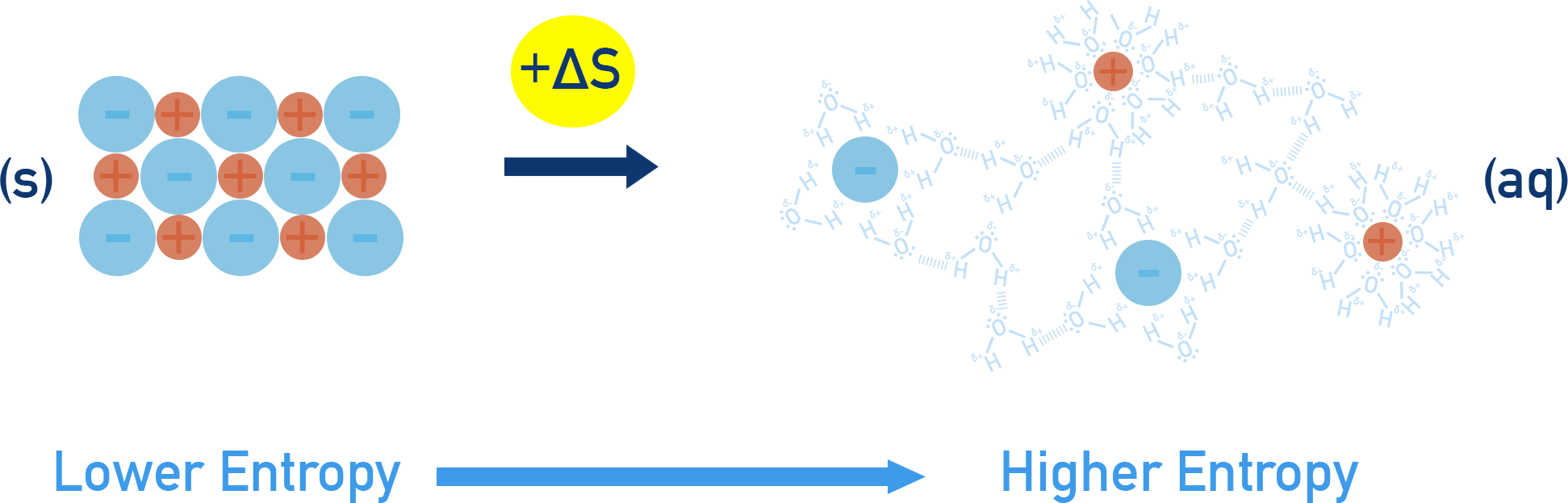
Dissolving a crystalline solid into solution increases disorder.
More gas particles formed

Reactions where the number of gaseous molecules increases show a big jump in entropy.
Examples:
N2(g) + 3H2(g) → 2NH3(g): Entropy decreases (fewer gas particles).
CaCO3(s) → CaO(s) + CO2(g): Entropy increases (gas formed).
The opposite is also true for all the above.
Table for Prediciting ΔS
| Process | Effect on Entropy |
|---|---|
| Melting / Boiling | Increase |
| Condensation / Freezing | Decrease |
| Dissolution of solid into liquid | Increase |
| Gas formation | Increase |
| Decrease in number of gas moles | Decrease |
Calculating Entropy Change (ΔS⦵)
Every substance, in a given state, has a standard entropy value (S⦵).
We can use the standard entropy values (S⦵) for each substance in a reaction (usually given in tables in the data booklet) to determine the entropy change, ΔS, that occurs.
Formula: ΔS = ΣS⦵(products) – ΣS⦵(reactants)
Step-by-step:
- Multiply each S⦵ value by the number of moles in the balanced equation.
- Add up all the S⦵ values for the products.
- Do the same for the reactants.
- Subtract reactant total from product total.

Don’t forget the molar ratios of everything in the equation and keep workings very clear. Also, make sure you are using a substance’s S⦵ value for the correct state (for example, H2O(l) has a different S⦵ to H2O(g)).
Calculate ΔSsystem for the reaction 2H2(g) + O2(g) → 2H2O(l).
- Given: S⦵(H2O(l)) = 70 J mol⁻¹ K⁻¹, S⦵(H2(g)) = 131 J mol⁻¹ K⁻¹, S⦵(O2(g)) = 205 J mol⁻¹ K⁻¹
- ΔS = [2 × 70] – [2 × 131 + 1 × 205]
- ΔS = 140 – (262 + 205) = 140 – 467 = –327 J mol⁻¹ K⁻¹
Entropy decreases in this reaction.
Entropy of a Perfect Crystal at 0 K
At absolute zero (0 K), a perfect crystal has zero entropy.
This is because there is only one way to arrange the particles, giving 'complete' order. This concept is the basis of the Third Law of Thermodynamics.
Why is the entropy of a perfect crystal at 0 K predicted to be zero?
At 0 K, the particles in a perfect crystal are in complete order with only one possible arrangement and no movement. Since entropy measures disorder (or, more correctly, the number of possible microstates), this total order means the entropy is zero.
Summary
- Entropy (S) measures disorder and energy dispersal in a system.
- Entropy order: gases > liquids > solids.
- Entropy increases with melting, boiling, gas formation, and dissolution.
- Entropy decreases with condensation, freezing, or fewer gas particles.
- ΔS⦵ is calculated using standard entropy values of products minus reactants.
- Perfect crystals at 0 K have zero entropy.
