AP | A-Level | IB | NCERT 11 + 12 – FREE NOTES, RESOURCES AND VIDEOS!
IB® (SL and AHL)
YouTube Channel
YouTube Channel
@chemistry.student
S1.1 - Introduction to the particulate nature of matter S1.2 - The nuclear atom S1.3 - Electron configurations S1.4 - Counting particles by mass - The mole S1.5 - Ideal gases S2.1 - The ionic model S2.2 - The covalent model S2.3 - The metallic model S2.4 - From models to materials S3.1 - The periodic table - Classification of elements S3.2 - Functional groups - Classification of organic compounds R1.1 - Measuring enthalpy changes R1.2 - Energy cycles in reactions R1.3 - Energy from fuels R1.4 - Entropy and spontaneity AHL R2.1 - How much? The amount of chemical change R2.2 - How fast? The rate of chemical change R2.3 - How far? The extent of chemical change R3.1 - Proton transfer reactions R3.2 - Electron transfer reactions R3.3 - Electron sharing reactions R3.4 - Electron-pair sharing reactions

S1.5 - Ideal gases

1.5.1 Ideal Gas Model 1.5.2 Limitations of Ideal Gas Model 1.5.3 Gas Laws and Molar Volumes of Ideal Gases 1.5.4 Ideal Gas Equation, PV=nRT

The Ideal Gas Equation and Gas Law Calculations

Specification Reference S1.5.4

Quick Notes

  • The ideal gas equation: pV = nRT
    • p = pressure (in Pa)
    • V = volume (in m³)
    • n = amount in moles (mol)
    • R = 8.31 J mol⁻¹ K⁻¹ (gas constant)
    • T = temperature (in K)
  • All units must be SI units:
    • Pressure: Pa (1 kPa = 1000 Pa)
    • Volume: m³ (1 dm³ = 0.001 m³ or 1000 cm³ = 1 dm³)
    • Temperature: K (K = °C + 273)
  • The combined gas law: P₁V₁ ÷ T₁ = P₂V₂ ÷ T₂

Full Notes

Recap – The Ideal Gas Equation

The ideal gas equation links the four key properties of a gas:

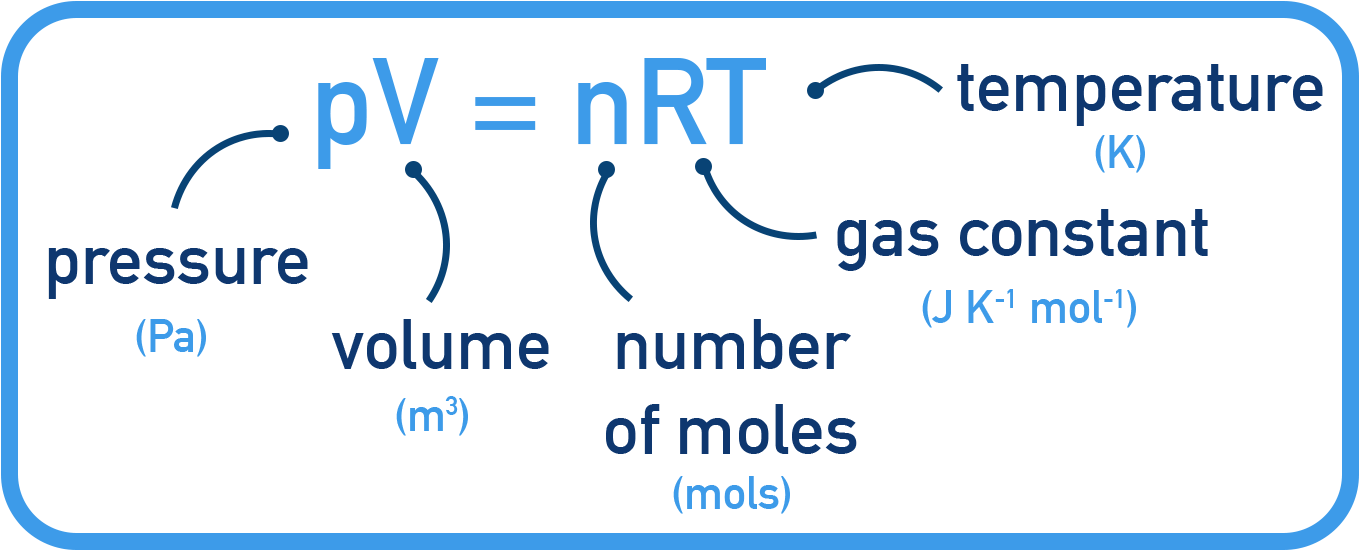
IB Chemistry diagram of the ideal gas equation showing pV = nRT and its variables.
Photo of Matt
Matt’s exam tip

Always check your units carefully. Pressure must be in Pa, volume in m³, and temperature in K. Convert kPa to Pa, dm³ to m³, and °C to K before using the equations.


Worked Example

Calculate the volume in dm³ occupied by 0.250 mol of CO₂ at 298 K and 100 kPa.

  1. Convert units: Pressure = 100 kPa = 100,000 Pa Temperature = 298 K R = 8.31 J mol⁻¹ K⁻¹ n = 0.250 mol
  2. Use the formula: V = nRT ÷ p = (0.250 × 8.31 × 298) ÷ 100,000 = 0.00619 m³ = 6.19 dm³

The Combined Gas Law

The combined gas law is used when the amount of gas (n) stays constant, but pressure, volume, or temperature changes:

P₁V₁ ÷ T₁ = P₂V₂ ÷ T₂

This is useful for comparing a gas before and after a change in conditions.

Worked Example

A gas has a volume of 1.50 dm³ at 300 K and 100 kPa. What will its volume be at 400 K and 120 kPa?

  1. Convert units: V₁ = 1.50 dm³ = 0.00150 m³ T₁ = 300 K, P₁ = 100,000 Pa T₂ = 400 K, P₂ = 120,000 Pa
  2. Rearrange the combined gas law: V₂ = (P₁ × V₁ × T₂) ÷ (P₂ × T₁)
  3. Plug in values: V₂ = (100,000 × 0.00150 × 400) ÷ (120,000 × 300) = 0.00167 m³ = 1.67 dm³

Summary