The Ionic Product Constant of Water, K_w

Specification Reference R3.1.5

Quick Notes

Water ionizes slightly: H₂O ⇌ H⁺ + OH⁻
The ionic product constant of water is: K_w = [H⁺][OH⁻]
At 298 K, K_w = 1.0 × 10⁻¹⁴ mol² dm⁻⁶
In pure water: [H⁺] = [OH⁻] = 1.0 × 10⁻⁷ mol dm⁻³ and pH = 7 (neutral)
If [H⁺] > [OH⁻] → acidic solution
If [H⁺] < [OH⁻] → basic solution
As temperature increases, K_w increases meaning more ionization of water

Full Notes

The Ionic Product of Water (Kw)

In water, a very small percentage of molecules ionise, releasing H⁺ and OH⁻ ions into solution.

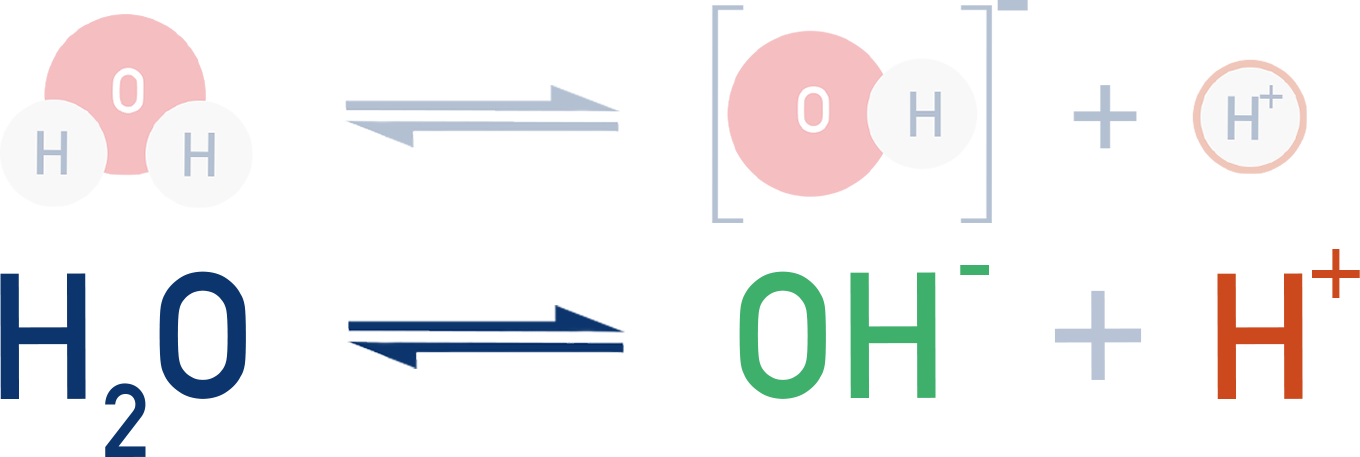
IB Chemistry diagram showing ionisation of water into H⁺ and OH⁻ ions with equilibrium arrows.

This is a reversible process and an equilibrium is established.

The equilibrium constant for this is:

IB Chemistry expression showing Kw = [H⁺][OH⁻] with units mol² dm⁻⁶.

At 298 K: K_w = 1.0 × 10⁻¹⁴ mol² dm⁻⁶

K_w is key for finding pH of bases, because strong bases increase [OH⁻].

pH of Strong Bases

For a strong base like NaOH, we don’t directly know the concentration of H⁺ ions in solution. However, we can use K_w to determine [H⁺]:

[OH⁻] = concentration of the base
Use K_w to find [H⁺]:

Worked Example

Find the pH of an NaOH solution with a concentration of 0.010 mol dm⁻³:

[OH⁻] = 0.010
[H⁺] = 1.0 × 10⁻¹⁴ / 0.010 = 1.0 × 10⁻¹²
pH = –log(1.0 × 10⁻¹²) = 12.00

Understanding Solution Type from [H⁺] and [OH⁻]

Whether a solution is acidic or basic (alkaline) is based on the relationship between [H⁺] and [OH⁻]:

Neutral solution: [H⁺] = [OH⁻] (at 298 K this gives a pH of 7)
Acidic solution: [H⁺] > [OH⁻] (pH < 7 at 298 K)
Basic (alkaline) solution: [H⁺] < [OH⁻] (pH > 7 at 298 K)

K_w always equals [H⁺] × [OH⁻], so if one increases, the other must decrease.

Summary

K_w = [H⁺][OH⁻] defines the ionization of water.
At 298 K, K_w = 1.0 × 10⁻¹⁴ mol² dm⁻⁶.
Pure water has [H⁺] = [OH⁻] = 1.0 × 10⁻⁷ mol dm⁻³, giving pH 7.
Solutions with [H⁺] > [OH⁻] are acidic, and with [H⁺] < [OH⁻] are basic.
As temperature rises, K_w increases and pH decreases slightly.

Linked Course Question

Reactivity 2.3 — Linked Course Question

Why does the extent of ionization of water increase as temperature increases?

The forward direction for the ionization of water is an endothermic process:

H₂O(l) ⇌ H⁺(aq) + OH⁻(aq) ΔH = +

As temperature increases, the equilibrium shifts to the right to absorb the added heat (according to Le Châtelier’s principle). This means:

More water molecules ionize.
The concentrations of H⁺ and OH⁻ increase.
The ionization constant of water (K_w) increases.

So, the amount of ionization increases at higher temperatures because the system favours the production of more ions to counteract the temperature rise.

Note: Even though [H⁺] increases with temperature, pure water is still neutral at all temperatures because [H⁺] = [OH⁻]. However, the pH decreases slightly because it depends on [H⁺].

The Ionic Product Constant of Water, Kw