AP | A-Level | IB | NCERT 11 + 12 – FREE NOTES, RESOURCES AND VIDEOS!
IB® (SL and AHL)
YouTube Channel
YouTube Channel
@chemistry.student
S1.1 - Introduction to the particulate nature of matter S1.2 - The nuclear atom S1.3 - Electron configurations S1.4 - Counting particles by mass - The mole S1.5 - Ideal gases S2.1 - The ionic model S2.2 - The covalent model S2.3 - The metallic model S2.4 - From models to materials S3.1 - The periodic table - Classification of elements S3.2 - Functional groups - Classification of organic compounds R1.1 - Measuring enthalpy changes R1.2 - Energy cycles in reactions R1.3 - Energy from fuels R1.4 - Entropy and spontaneity AHL R2.1 - How much? The amount of chemical change R2.2 - How fast? The rate of chemical change R2.3 - How far? The extent of chemical change R3.1 - Proton transfer reactions R3.2 - Electron transfer reactions R3.3 - Electron sharing reactions R3.4 - Electron-pair sharing reactions

S1.4 - Counting particles by mass - The Mole

1.4.1 The Mole and Avagadro's Constant 1.4.2 Relative Atomic Mass (Ar) and Relative Formula Mass (Mr) 1.4.3 Molar Mass, Mass and the Mole 1.4.4 Empirical and Intermolecular Formulae 1.4.5 Molar Concentration and Solution Calculations 1.4.6 Avagadro's Law and Gas Volumes

Molar Mass, Mass and the Mole

Specification Reference S1.4.3

Quick Notes

  • Molar mass (M) is the mass of 1 mole of a substance.
    • Units: g mol⁻¹
  • We can link mass, moles, and molar mass, using the formula: n = m ÷ M
    • n = amount in moles
    • m = mass in grams
    • M = molar mass (g mol⁻¹)
  • Rearranged versions: m = n × M and M = m ÷ n
  • Molar mass is numerically equal (same number) to the relative atomic or formula mass (Mr) but includes units.

Full Notes

What Is Molar Mass (M)?

The molar mass of a substance is the mass of one mole of that substance.

It is expressed in grams per mole (g mol⁻¹).

Molar mass is numerically the same as the relative atomic mass (Ar) or relative formula mass (Mr), but with units added.

Examples:
Hydrogen (H): Ar = 1.01 meaning M = 1.01 g mol⁻¹
Water (H₂O): Mr = 18.02 meaning M = 18.02 g mol⁻¹

The Relationship: n = m ÷ M

Moles, mass and molar mass can all be linked by this equation:

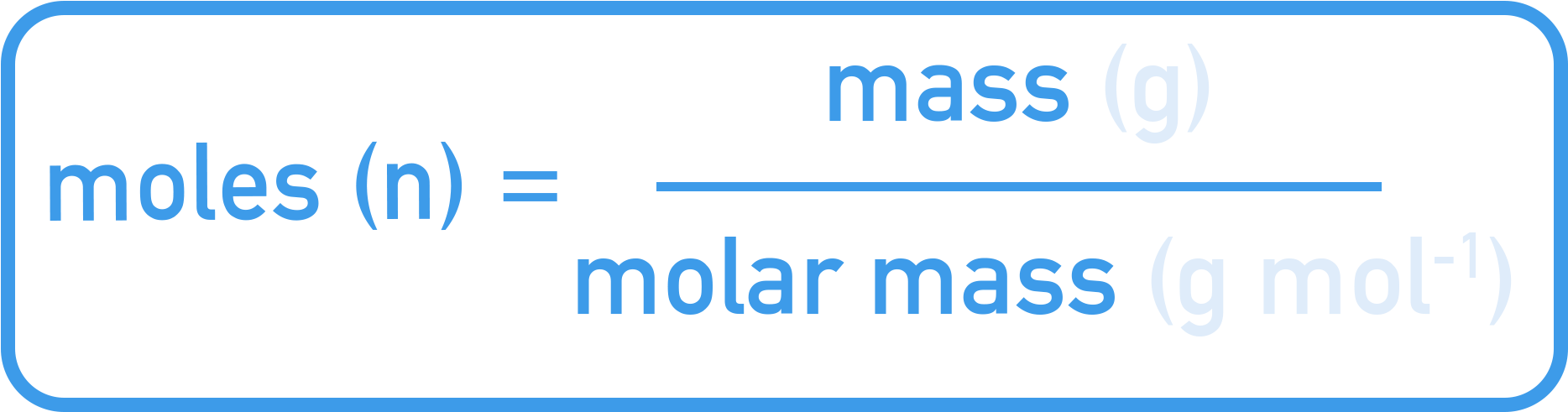
IB Chemistry diagram linking moles, mass, and molar mass with n = m divided by M.

We can rearrange this to find any unknown:

Worked Example

Finding moles from mass

  1. Given: 36.04 g of water (H₂O), M(H₂O) = 18.02 g mol⁻¹
  2. n = m ÷ M = 36.04 ÷ 18.02

Answer: 2.00 mol


Worked Example

Finding mass from moles

  1. Given: 0.50 mol of sodium chloride (NaCl), M(NaCl) = 58.44 g mol⁻¹
  2. m = n × M = 0.50 × 58.44

Answer: 29.22 g


Worked Example

Finding molar mass

  1. Given: 0.25 mol of a compound has a mass of 11.5 g
  2. M = m ÷ n = 11.5 ÷ 0.25

Answer: 46.0 g mol⁻¹

Combining with Avogadro’s Constant

We can convert between number of particles and moles using Avogadro’s constant:

IB Chemistry relationship between moles and number of particles using Avogadro’s constant.

This allows us to go from mass to moles to particles.

Summary

Linked Question

Reactivity 2.1 – Linked Course Question

How can molar masses be used with chemical equations to determine the masses of the products of a reaction?

Balanced chemical equations show the stoichiometric ratios between reactants and products. By using the molar masses of substances, these ratios can be converted into measurable quantities. The general process is:

  1. Use the given mass of a reactant to calculate its amount in moles.
  2. Apply the mole ratio from the balanced equation to find the moles of the desired product.
  3. Multiply the product’s moles by its molar mass to obtain its mass.

This method links the theoretical relationships in an equation to real laboratory quantities, allowing the prediction of product yields or reactant requirements.