The Arrhenius Factor (A) HL Only
Quick Notes
- In the Arrhenius equation, A is the frequency factor – it reflects how often collisions occur with the correct orientation to react.
- Arrhenius equation:

- Linear form (used for graphing):

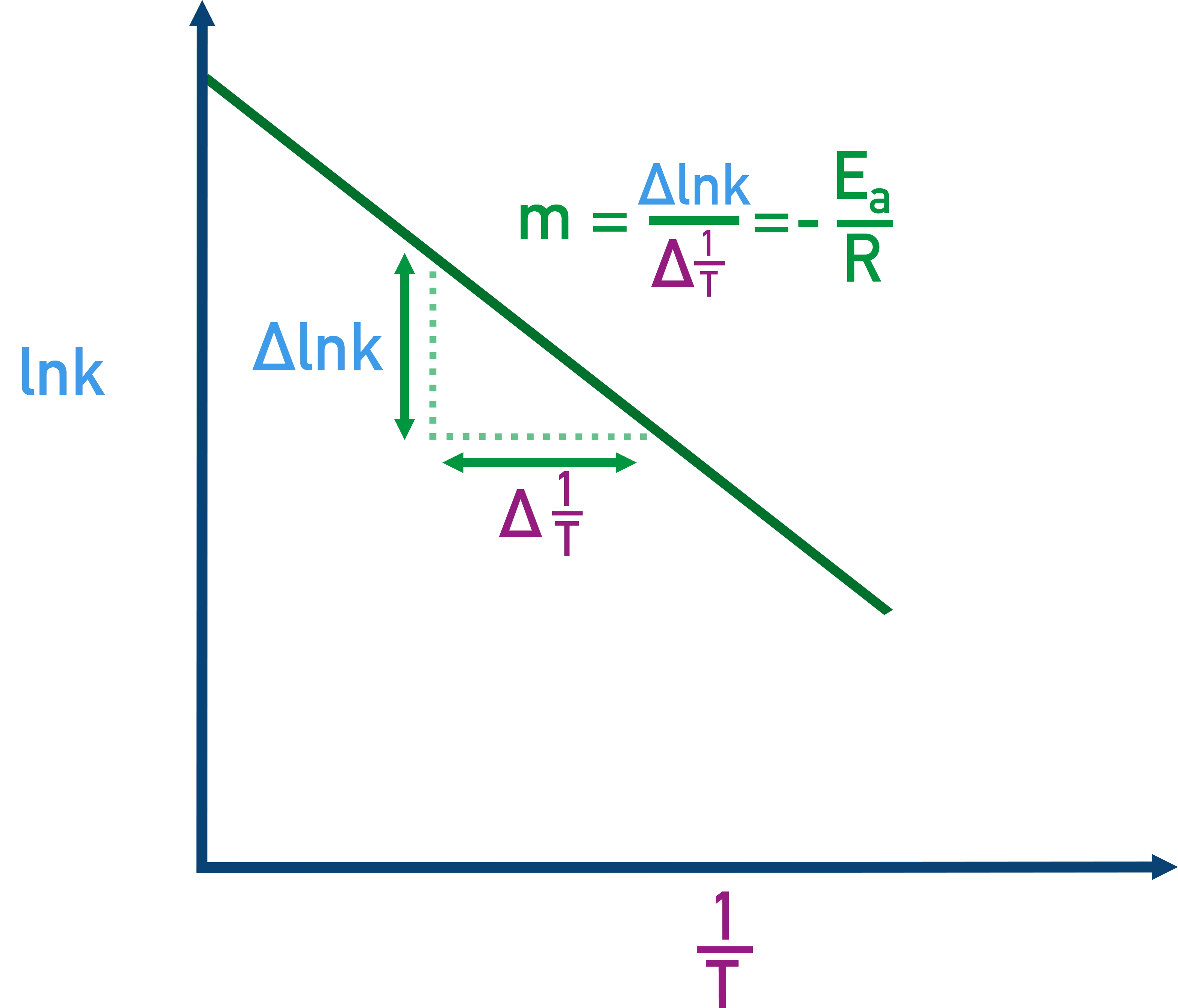
- A graph of ln k vs 1/T gives a straight line:
- Slope = –Ea / R
- Intercept = ln A
Full Notes
Background theory to the Arrhenius Equation has been covered here - make sure you are comfortable with it before tackling this page.
What Is the Arrhenius Factor, A?
A (the pre-exponential factor) reflects how often particles collide with the correct orientation to react.
While Ea (activation energy) represents the energy barrier, A indicates the frequency and effectiveness of collisions.

You can think of A as the maximum possible theoretical rate — if all particles had enough energy, the rate would simply be A × [reactants]. See this video for more: https://youtu.be/kj4laup0kvs
Performing Arrhenius Equation Calculations
Calculate Activation Energy (Ea) Using Two Rate Constants
- A reaction has the following rate constants, k, at 300K and 350K. Determine the activation energy, Ea, for the reaction.
At 300K, k = 2.5 × 10−3 s−1
At 350K, k = 5.0 × 10−3 s−1 - Use:
ln (k2 / k1) = (−Ea / R) × (1/T2 − 1/T1)
ln (5.0 × 10−3 / 2.5 × 10−3) = (−Ea / 8.31) × (1/350 − 1/300)
ln 2 = (−Ea / 8.31) × (−4.76 × 10−4) - Ea = (ln 2 × 8.31) / (4.76 × 10−4)
Ea = 12 110 J mol−1 = 12.1 kJ mol−1

when using the Arrhenius equation in calculations, don’t forget units of activation energy (Ea) are kJ mol−1! The gas constant, R, has units of J K−1 mol−1, meaning you must convert any calculated Ea value to kJ (divide by 1000).
Using Arrhenius Graph to Find Ea and A
The gradient of an Arrhenius plot is −Ea÷R which can be rearranged to find activation energy (Ea).
By plotting ln k vs. 1÷T, we can also use the intercept of the line across the y axis to find A.
Summary
- The Arrhenius equation links temperature and rate constant.
- Rate constants increase with temperature.
- Graphing ln k vs 1/T gives a straight line from which Ea and A can be determined.
- The Arrhenius factor A tells us the frequency of properly oriented collisions between reactants.
- Ea and A can be determined from a graph of ln k vs 1/T using experimental data.
