AP | A-Level | IB | NCERT 11 + 12 – FREE NOTES, RESOURCES AND VIDEOS!
IB® (SL and AHL)
YouTube Channel
YouTube Channel
@chemistry.student
S1.1 - Introduction to the particulate nature of matter S1.2 - The nuclear atom S1.3 - Electron configurations S1.4 - Counting particles by mass - The mole S1.5 - Ideal gases S2.1 - The ionic model S2.2 - The covalent model S2.3 - The metallic model S2.4 - From models to materials S3.1 - The periodic table - Classification of elements S3.2 - Functional groups - Classification of organic compounds R1.1 - Measuring enthalpy changes R1.2 - Energy cycles in reactions R1.3 - Energy from fuels R1.4 - Entropy and spontaneity AHL R2.1 - How much? The amount of chemical change R2.2 - How fast? The rate of chemical change R2.3 - How far? The extent of chemical change R3.1 - Proton transfer reactions R3.2 - Electron transfer reactions R3.3 - Electron sharing reactions R3.4 - Electron-pair sharing reactions

R3.1 - Proton transfer reactions

3.1.1 Bronsted-Lowry Acid-Base Theory 3.1.2 Conjugation Acid-Base Pairs 3.1.3 Acid-Base Behaviour and Oxides 3.1.4 pH and [H+] 3.1.5 Kw and pH of Water 3.1.6 Strong Vs. Weak Acids and Bases 3.1.7 Neutralization Reaction 3.1.8 pH Curves 3.1.9 pH and [OH-] (AHL) 3.1.10 Ka, Kb, pKa and pKb (AHL) 3.1.11 Ka x Kb = Kw (AHL) 3.1.12 pH of Salt Solutions (AHL) 3.1.13 pH Curves for Acid-Base Reaction (AHL) 3.1.14 Acid-Base Indicators (AHL) 3.1.15 Indicators and Titration Points (AHL) 3.1.16 Buffer Solutions (AHL) 3.1.17 pH of Buffer (AHL)

Ka × Kb = Kw HL Only

Specification Reference R3.1.11

Quick Notes

  • For a conjugate acid–base pair, Ka (for the acid) multiplied by Kb (for its conjugate base) equals Kw:
    Ka × Kb = Kw
  • At 298 K, Kw = 1.00 × 10⁻¹⁴
  • If you know Ka, you can calculate Kb, and vice versa.
  • Useful in problems involving weak acids and bases.
  • Logarithmic form: pKa + pKb = 14 (at 298K)
  • No need for quadratic equations – approximations can simplify when Ka or Kb is very small.

Full Notes

Deriving the Relationship

The relationship Ka × Kb = Kw applies to conjugate acid–base pairs and is derived from the equilibrium expressions for acid and base dissociation.

Weak acid HA

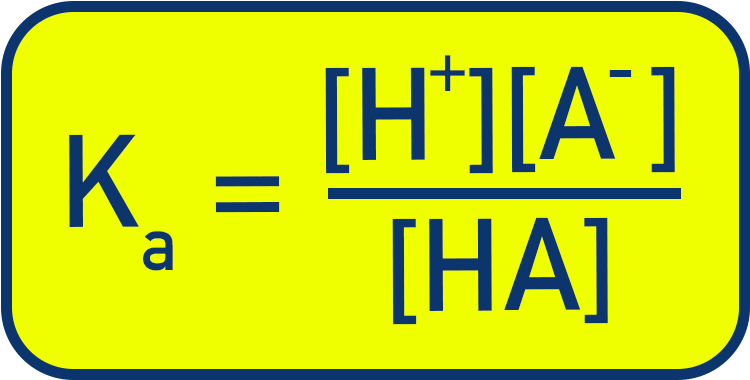
IB Chemistry equation showing weak acid HA dissociating into H⁺ and A⁻. IB Chemistry expression for K<sub>a</sub>, the equilibrium constant for dissociation of a weak acid.

Conjugate base A⁻

IB Chemistry equation showing conjugate base A⁻ reacting with water to form OH⁻ and HA. IB Chemistry expression for K<sub>b</sub>, the equilibrium constant for base hydrolysis.

Multiplying these together:

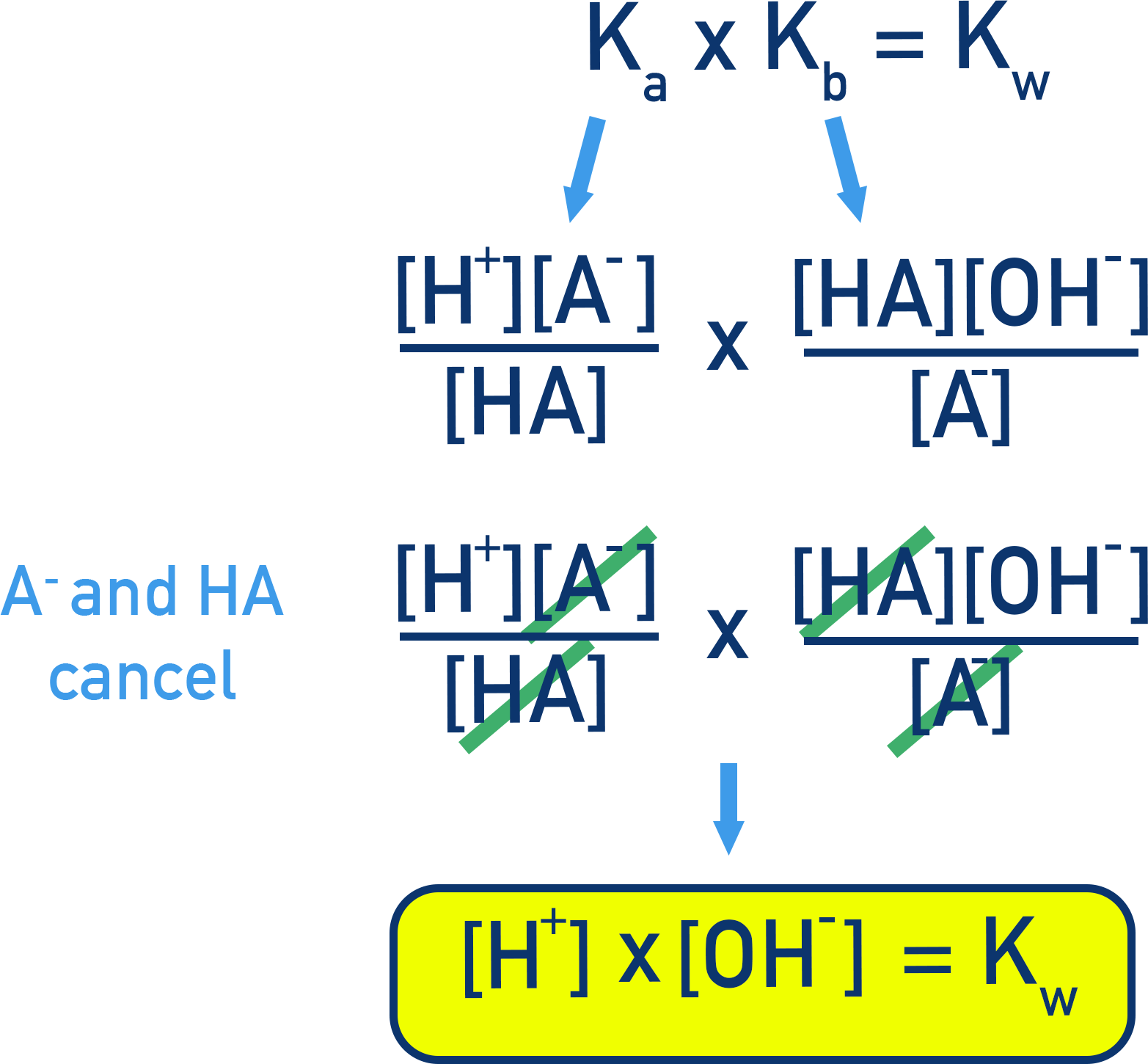
IB Chemistry derivation showing K<sub>a</sub> × K<sub>b</sub> = K<sub>w</sub>.

Logarithmic Form

At 298 K: Kw = 1.00 × 10⁻¹⁴

and pKa + pKb = 14 (at 298 K).

This comes from the relationship: Ka × Kb = Kw, where Kw = 1 × 10⁻¹⁴ at 298 K.

Taking logs:

So: pKa + pKb = –log₁₀(Ka) – log₁₀(Kb) = –log₁₀(Ka × Kb) = –log₁₀(Kw) = 14

Photo of Matt
Matt’s exam tip

Remember this equation is only true at 298 K, when Kw is 1 × 10⁻¹⁴. If temperature changes, the Kw value also changes. See Kw.

Summary

Linked Course Question

Reactivity 2.3 — Linked Course Question

How can we simplify calculations when equilibrium constants Ka and Kb are very small?

When Ka or Kb values are very small (typically < 10⁻⁴), only a tiny amount of the acid or base ionizes or dissociates at equilibrium. This allows us to assume that the initial concentration of the acid or base is approximately the same as its equilibrium concentration.